◆熊本県 mit さんからの解答。
【問題1】
ライツアウトには次の特徴があります。
ある答えで、偶数回押したボタンは押す必要はなく、奇数回押したボタンは1回押せばよいことになります。
(これを『性質a』とします)
これを利用すれば最短手数でなくても基本図に戻せる答えが見つかれば最短手数に近い手数の解を得る事ができます。
下の図はこれを利用して得られた結果の一例です。
●→押すボタン、○→押さないボタン
●●○●●●○○○●○●●●●○● ○○●○●○○●○○●○○○●●○ ●●○○○○○●●○○○○○●○● ○○●○●○○●○●○○●●○●○ ●○○○●●○●○○○●●●○○● ●●○●●○○○●●○○○●●○○ ●○●○●○●○○○○●●●○●○しかし、これだけでは最短手数を見つける事ができない場合があるのもまた事実です。
パターン1 ●●○●●○●●○●●○●●○●● ○○○○○○○○○○○○○○○○○ ●●○●●○●●○●●○●●○●● ○○○○○○○○○○○○○○○○○ ●●○●●○●●○●●○●●○●● ○○○○○○○○○○○○○○○○○ ●●○●●○●●○●●○●●○●● パターン2 ●○○○●○●○○○●○●○○○● ●●○●●○●●○●●○●●○●● ●○○○●○●○○○●○●○○○● ○○○○○○○○○○○○○○○○○ ●○○○●○●○○○●○●○○○● ●●○●●○●●○●●○●●○●● ●○○○●○●○○○●○●○○○● パターン3 ○●○●○○○●○●○○○●○●○ ●●○●●○●●○●●○●●○●● ○●○●○○○●○●○○○●○●○ ○○○○○○○○○○○○○○○○○ ○●○●○○○●○●○○○●○●○ ●●○●●○●●○●●○●●○●● ○●○●○○○●○●○○○●○●○これらのパターンに従ってボタンを押すと、2度押したボタンが一つもないのにもかかわらず、押す前の状態に戻ってしまうという現象が起こります。
いずれも押すボタンの数は48個なので、求めた解とこれらのパターンと比べてみて、もし押すボタンの重複が24個より多い場合、性質aから求めた解よりも少ない手数の解を得られることになります。
ちなみにちょうど24個の場合は別解を求める事ができます。
この場合の押すボタンの重複は上二つは24個、一番下は20個なので、これより少ない手数は見つけられないことになります。
よって解は下の図の通り。(54手)
●●○●●●○○○●○●●●●○● ○○●○●○○●○○●○○○●●○ ●●○○○○○●●○○○○○●○● ○○●○●○○●○●○○●●○●○ ●○○○●●○●○○○●●●○○● ●●○●●○○○●●○○○●●○○ ●○●○●○●○○○○●●●○●○Full Pushによって生成されるパターンを基本図に戻すのに必要な手数に41手の解があることから、
もしかしたらそれを使ったらもっと少ない手数の解が見つかるかもしれません。
◆東京都 oidon さんからの解答。
セル(X,Y)のライトが点灯しており,Xより左は全てスイッチ操作により消灯しているものとする.
ただしX>1とする.
このとき(X,Y)を消すためには(X+1,Y)のスイッチを押さなければならない.
このようにして左から順番に消すことを考えると,
最も左の列のスイッチを押すパターン(28=256)通りを調べれば全ての解が得られることになる.
そこで以下のプログラムによって全ての場合を考え,全てのライトが消灯する中で最も手数の少ないものを解とした.
この結果得られた最小手数は50手であり,解は
(1, 4), (1, 6), (2, 3), (2, 4), (2, 6), (2, 7), (3, 4), (3, 6), (3, 7), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (5, 3), (6, 1), (6, 5), (7, 1), (7, 2), (7, 3), (7, 4), (7, 5), (7, 6), (8, 6), (9, 2), (9, 3), (10, 6), (10, 7), (11, 1), (11, 2), (11, 3), (11, 4), (11, 5), (11, 7), (12, 1), (12, 5), (12, 7), (13, 3), (14, 5), (14, 6), (15, 1), (15, 3), (16, 3), (16, 5), (16, 6), (16, 7), (17, 2), (17, 4), (17, 6), (17, 7)となった.なお,計算時間は0.5秒である.
#!/usr/bin/python
import re, string, sys, os
data =\
"""
..X...XXXXX.XXXXX
.XXX..X...X.X...X
..X...X...X.X...X
..X...XXXXX.XXXXX
..X.......X.....X
..X...X...X.X...X
.XXX..XXXXX.XXXXX
"""
regex = re.compile( "[^\\.\\w]+", re.M )
class Field:
def __init__( self, data ):
lines = regex.split( data )
field = []
min_columns = 999
for i in range( len( lines ) ):
columns = len( lines[ i ] )
if columns > 0:
if columns < min_columns:
min_columns = columns
pass
row = []
for x in lines[ i ]:
if x == "X":
row.append( 1 )
else:
row.append( 0 )
pass
pass
field.append( row )
pass
pass
self.__field = field
self.__rows = len( field )
self.__columns = min_columns
pass
def __repr__( self ):
str = ""
for row in self.__field:
line = ""
for x in row:
if x == 0:
line += " "
elif x == 1:
line += "O"
pass
pass
str += line + "\n"
pass
return str
def push( self, x, y ):
left = x - 1
right = x + 1
top = y - 1
bottom = y + 1
if x < 0 or x >= self.__columns or y < 0 or y >= self.__rows:
return
if left < 0 : left = 0
if right >= self.__columns : right = self.__columns - 1
if top < 0 : top = 0
if bottom >= self.__rows : bottom = self.__rows - 1
v = top
while v <= bottom:
self.__field[ v ][ x ] = 1 - self.__field[ v ][ x ]
v += 1
pass
h = left
while h <= right:
if x != h:
self.__field[ y ][ h ] = 1 - self.__field[ y ][ h ]
pass
h += 1
pass
return
def get_columns( self ):
return self.__columns
def get_rows( self ):
return self.__rows
def is_on( self, x, y ):
if x < 0 or x >= self.__columns or y < 0 or y >= self.__rows:
return False
return ( self.__field[ y ][ x ] == 1 )
def is_off( self, x, y ):
if x < 0 or x >= self.__columns or y < 0 or y >= self.__rows:
return False
return ( self.__field[ y ][ x ] == 0 )
def is_all_off( self ):
for row in self.__field:
for cell in row:
if cell != 0:
return False
pass
pass
return True
pass
f = Field( data )
print f
code = 0
min_steps = f.get_columns() * f.get_columns()
answer = None
while code < 256:
f = Field( data )
bit = 1
num_switch = 0
pushed = []
for i in range( 0, 8 ):
if ( bit & code ) != 0:
f.push( 0, i )
num_switch += 1
pushed.append( ( 1, i + 1 ) )
pass
bit *= 2
pass
for x in range( 1, f.get_columns() ):
for y in range( 0, f.get_rows() ):
if f.is_on( x - 1, y ):
f.push( x, y )
pushed.append( ( x + 1, y + 1 ) )
num_switch += 1
pass
pass
pass
if f.is_all_off():
if min_steps > num_switch:
min_steps = num_switch
answer = pushed
pass
code += 1
pass
print min_steps
print answer
◆東京都 ぽこぺん さんからの解答。
【Lights Out の性質】
(1) 座標(定義): 盤面を m×n の長方形とし,行列方式(左上からの行・列の番号)で点に座標を付ける。
(2) 被覆(定義): 点 (i,j) を中心とする十字形
C(i,j) = {(i, j), (i-1, j), (i+1, j), (i, j-1), (i, j+1)}
を被覆と呼ぶ。
ただし,被覆の一部が盤面の外にはみ出すときには,その部分を無視する。
(3) 反転操作(定義): 被覆 C(i,j) に覆われる点の on/off を逆にする操作を,C(i,j) に対応する反転操作と呼ぶ。
なお,被覆の記号を代用して,その被覆に対応する 1 回の反転操作も表す。
(4) 偶奇性・縮退: 初期状態から始めて有限回の反転操作を行った結果,一つの点の on/off の状態は,その上に乗る被覆の枚数のみによって決まり,反転操作の順序によらない。
被覆の枚数が偶数ならば初期状態と同じ,奇数ならば初期状態の反対である。
したがって,同じ点を中心とする被覆(同一の被覆)が複数枚あるとき,偶数枚ならばその被覆は 0 枚と同じ,奇数枚ならば 1 枚と同じと考えてよい。
これを縮退と呼ぶことにする。
以下では被覆は縮退した形で考える。
(5) 重ね合わせの原理: 状態が on の点の集合 A,B が共有点を持たないとき,それぞれに有限回の反転操作 R を施した
結果(の on の点の集合)を A',B' とすると,
A∪B に R を施した結果は A' と B' の対称差 (A'∪B')-(A'∩B') となる。
(6) 可逆性: 盤面上の点の集合 S に対し,被覆の集合 {C(i,j) | (i,j)∈S} に対応する反転操作の集合により盤面の状態 A が状態 B に変わるとき,同じ反転操作の集合により B は A に変わる。
(7) 無限盤面の問題: 上下左右に無限に広がった盤面においては,その中の 1 点だけが on である初期状態から出発して,有限回の反転操作ですべての点を off にすることはできない。
(証明)所与の初期状態から始めて,同じ点を中心とする反転操作を複数回行わずに有限回の反転操作を行った結果,被覆が占める領域の最も外側の点は 1 枚だけの被覆により覆われるから,その領域には必ず on の点が含まれる。■
(8) 有限盤面の問題: 前項の結果,有限の盤面において,もし同じ初期状態から始めてすべての点を off にすることができたとすると,被覆が占める領域は必ず盤面の周辺(第 1 行,第 n 行,第 1 列,第 n 列の少なくとも 1 つ)と共有点を持つ。
【掃引操作】
(1) 掃引操作(定義): 盤面上のすべての on の点の集合 L に対して
j_max = max{j | (i, j)∈L}
によって定まる j_max が 1 より大きいとき,被覆の集合
{C(i,j_max - 1) | (i, j_max)∈L}
に対応する反転操作を 1 ステップとし,それを可能な限り繰り返す操作を,行方向の負の掃引操作と呼ぶ。
1 ステップごとに,j_max の値は 1 以上小さくなるので,この操作は有限回の繰り返しで終了する。
また,同様に行方向の正の掃引操作,列方向の正・負の掃引操作を定義する。
(2) 周辺配置(定義): 与えられた盤面上のすべての on の点の集合 L に対して,行方向の負の掃引操作により第 1 列に集められた on の点の集合 R_b(L) を L に対する第 1 列の周辺配置と呼ぶ。
同様に,それぞれ第 n 列,第 1 行,第 m 行の周辺配置 R_f(L),C_b(L),C_f(L) を定義する。
【問題の解答】
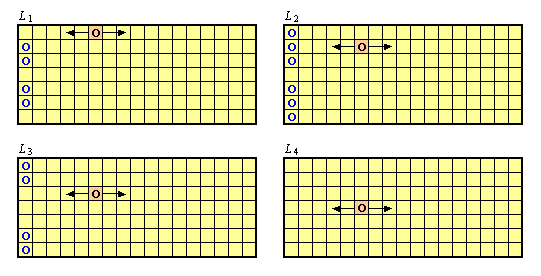
(1) m = 7, n = 17 の場合,第 6 列の各点 L_i = {(i, 6)} に対する第 1 列と第 n 列の周辺配置は次図のようになる。
ただし,i > 4 に対する周辺配置は,i < 4 の図の上下を対称移動したものだから,図は省略する。
たとえば,L_1 に対しては,第 1 列の周辺配置は
M_r-(L_1) = {(2, 1), (3, 1), (5, 1), (6, 1)} の 4 点となり,
第 n 列の周辺配置は M_r+(L_1) = φ(空)となる。

(2) 解の存在定理: 第 1 列の周辺配置に (4, 1) が含まれず,上下対称であれば,その問題には解が存在する。
(証明)周辺配置が {(1, 1), (7, 1)} であるとき,重ね合わせの原理により
L_1 ∪ L_2 からの負の掃引操作が存在する。
したがって,可逆性を用いれば,この周辺配置から L_1 ∪ L_2 を作ることができ,そこからの正の掃引操作で点を消去することができる。
一般に,
M_r-(L_1 ∪ L_2) = {(1, 1), (7, 1)}
M_r-(L_1 ∪ L_2 ∪ L_3) = {(2, 1), (6, 1)}
M_r-(L_2 ∪ L_3) = {(3, 1), (5, 1)}
および,この L_1,L_2,L_3 を それぞれ L_7,L_6,L_5 に個別に入れ替えた式が成立するから,定理が成り立つ。
(注)明らかに,この定理は第 17 列の周辺配置に対しても同様の形で成立する。
(3) 問題1(『199』)
問題の初期配置を I とする。このとき,
M_r-(I) = {(2, 1), (3, 1), (5, 1), (6, 1)}
となるので I には解が存在する。
行方向の負および正の掃引操作,さらに掃引操作に含まれない反転操作を行ってすべての点を off にすることができた操作の集合の例(大きさ50)を次に示す。
ただし,反転操作 C(i, j) を (i, j) と略記する。
{(1, 4), (1, 6), (1, 7), (1, 11), (1, 12), (1, 15), (2, 4), (2, 7), (2, 9), (2, 11),
(2, 17), (3, 2), (3, 4), (3, 5), (3, 7), (3, 9), (3, 11), (3, 13), (3, 15), (3, 16),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 7), (4, 11), (4, 17), (5, 4), (5, 6), (5, 7),
(5, 11), (5, 12), (5, 14), (5, 16), (6, 1), (6, 2), (6, 3), (6, 7), (6, 8), (6, 10),
(6, 14), (6, 16), (6, 17), (7, 2), (7, 3), (7, 10), (7, 11), (7, 12), (7, 16), (7, 17)}
この解も含め,解となる操作集合の例を下図に掲げる。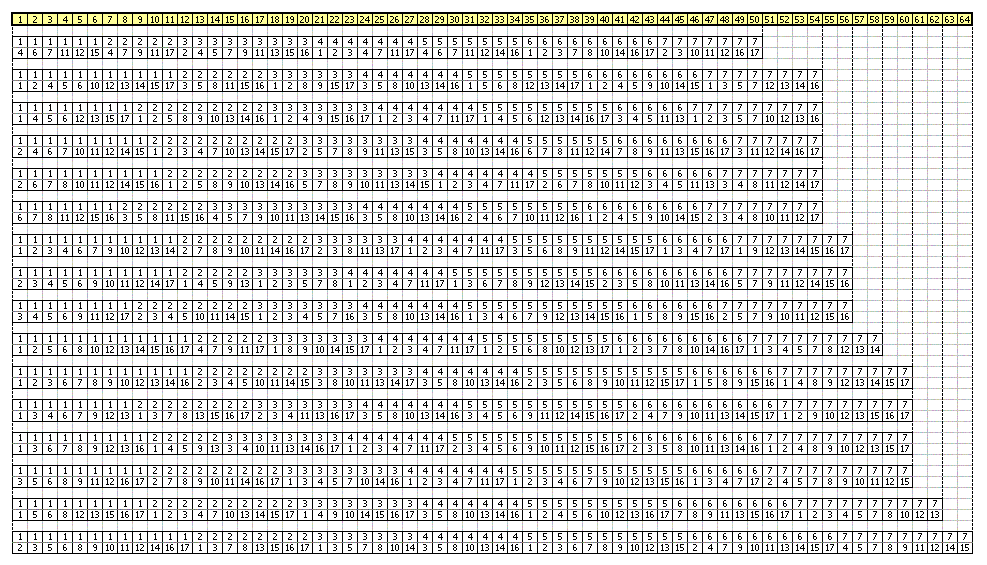
(4) 問題2(『200』)
問題の初期配置を I とする。このとき,
M_r-(I) = {(1, 1), (3, 1), (6, 1), (7, 1)}
となるので定理の条件を満たしていない。
このうち,定理の対称性を崩しているのは点 (3, 1) と (6, 1) であるが,
M_r-({(7, 5)}) = {(3, 1)}
M_r-({(2, 11)}) = {(6, 1)}
であるから,I に対して点 (7, 5) と (2, 11) の on/off を反転させたものは定理の条件を満たす。
このとき,初期配置は
□■■■□□□■■■□□□■■■□ ■□□□■□■□□□□□■□□□■ □□□□■□■□□□■□■□□□■ □□□■□□■□□□■□■□□□■ □□■□□□■□□□■□■□□□■ □■□□□□■□□□■□■□□□■ ■■■■□□□■■■□□□■■■□となり,これに対して大きさ 45 の次のような解の例がある。
{(1, 3), (1, 5), (1, 7), (1, 11), (1, 14), (2, 4), (2, 5), (2, 7), (2, 9), (2, 11),
(2, 12), (2, 13),(2, 16), (3, 1), (3, 7), (3, 9), (3, 11), (3, 12), (3, 13), (3, 15),
(3, 16), (4, 1), (4, 2), (4, 4), (4, 6), (4, 7), (4, 16), (5, 1), (5, 8), (5, 9),
(5, 12), (6, 3), (6, 4), (6, 6), (6, 7), (6, 10), (6, 12), (6, 16), (6, 17), (7, 1),
(7, 7), (7, 10), (7, 11), (7, 15), (7, 17)}
【感想】
◆静岡県 medaka さんからの解答。
【問題1】
50手(Push位置を■で表す)
□□□■□■■□□□■■□□■□□ □□□■□□■□■□■□□□□□■ □■□■■□■□■□■□■□■■□ ■■■■□□■□□□■□□□□□■ □□□■□■■□□□■■□■□■□ ■■■□□□■■□■□□□■□■■ □■■□□□□□□■■■□□□■■【問題2】
少なくとも、2ケ所を修正する必要があります。
例えば、下図のように(3,a),(6,a)の2ケ所の位置を■に変更するのが、あまり修正が目立たなくてよいでしょう。
abcdefghijklmnopq 1□■■■□□□■■■□□□■■■□ 2■□□□■□■□□□■□■□□□■ 3■□□□■□■□□□■□■□□□■ 4□□□■□□■□□□■□■□□□■ 5□□■□□□■□□□■□■□□□■ 6■■□□□□■□□□■□■□□□■ 7■■■■■□□■■■□□□■■■□この図の解は、44手(以下のPushパターン)
□□■□□□□□■□■□□■□□□ □□□□□□□□□■■■■□□■□ ■□■□■□■□□□■■■□■■□ □□■□□□□■□□□□□□□■□ ■■□□■□■■■□□■□□□□□ □□■■■□■□□■□■□□□■■ □■□■■□■□□■■□□□■□■【おまけ】
最多手数は、68手。
68手の問題の1例 ■□□□□□□□□□□□□□□□■ □■■■■■■■■■■■■■■■□ □■■■■■■■■□□■□□■□■ ■□□□□■□□■□□■□□□□■ ■■■■□■□■■□■■■□■□□ □□□□■■■□□□■■■□□□□ □□□□■□■□□□■□■□□□□上記の問題の解 (Push パターン)
■■■■■■■■■■■■■■■■■ ■■■■■■■■■■■■■■■■■ ■■■■■■■■■■■■■■■■■ ■■■■■■■■■□□■□□■□□ □□□□□■□□□□□■□□□□□ □□□□□■□□□□□■□□□□□ □□□□□■□□□□□■□□□□□
◆東京都 明 さんからの解答。
【問題1】
Push数 50回
手順
( 4, 1)→( 6, 1)→( 3, 2)→( 4, 2)→( 6, 2)→ ( 7, 2)→( 4, 3)→( 6, 3)→( 7, 3)→( 1, 4)→ ( 2, 4)→( 3, 4)→( 4, 4)→( 5, 4)→( 3, 5)→ ( 1, 6)→( 5, 6)→( 1, 7)→( 2, 7)→( 3, 7)→ ( 4, 7)→( 5, 7)→( 6, 7)→( 6, 8)→( 2, 9)→ ( 3, 9)→( 6,10)→( 7,10)→( 1,11)→( 2,11)→ ( 3,11)→( 4,11)→( 5,11)→( 7,11)→( 1,12)→ ( 5,12)→( 7,12)→( 3,13)→( 5,14)→( 6,14)→ ( 1,15)→( 3,15)→( 3,16)→( 5,16)→( 6,16)→ ( 7,16)→( 2,17)→( 4,17)→( 6,17)→( 7,17)→押したボタンの種類が同じであれば、順番には係わりません。
<求め方>
各ボタンに番号を付け、押したボタン毎に変化するパターンをすべて書き下ろすと、例えば7×3の場合は下記のようになり ます。
ただし、番号は(1,1)(2,1)・・・(6,3)(7,3)の順に付け、上から順に1〜21、左から順に1〜21とします。
1 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 1 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 1 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 1 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 1 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 1 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 1 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1ボタン毎に、押したときのパターンのオン、オフの変化は、上記パタ ーン(ベクトル)の排他的論理和であることを考えると、【問題1】は 与えられた初期パターンを上記ベクトルに展開することになります。
上記表から類推されるように、7×17=119のベクトルは明らかに一次独立な112個のベクトルと、7個(下の7個としました)のベクトルで構成されています。
以下は計算機の力を借りて考察しました。
7個のベクトルは3個の独立なベクトルと4個の従属なベクトルです。
従って【問題1】は初期パターンを115個から一意に選ばれたベクトルと4個の剰余ビットに展開することで解くことができます。
ただし4個の従属な(異なる)ベクトルがありますので、最終的には16通りの回答が得られます。
解を求めるためのプログラムを10進BASICで作りました。(下記)
【問題1】の回答はこの中で最小のものです。
LET AX=7 !配列の縦列数
LET AY=17 !配列の横列数
LET DM=AX*AY !ベクトルの次元
DIM B(DM+1,DM) !ベクトル配列表 DM+1:ワークエリア
DIM PR(AX+2,DM) !AX個のベクトルの構成メモリ AX+1,AX+2:ワークエリア
DIM BF(AX) !作業用バッファ
DIM BFC(AX) !作業用バッファ
DIM DR(5,2) !周辺位置指定メモリ
DATA 0,0,0,-1,-1,0,1,0,0,1
MAT READ DR
CALL becset !ベクトル配列表を求める
! CALL prnarr !ベクトル配列表出力
CALL convbe !AX個のベクトルを変換する
! CALL prnpro !AX個のベクトルの構成成分の出力
! CALL prnrem !AX個のベクトルの変換後出力
CALL caldim !AX個のベクトルの独立数を求める
! PRINT "独立数 :";ID !独立数出力
! CALL prnrem !AX個のベクトルの再変換後出力
REM 初期パターンの生成
DIM G(DM)
DATA 0,0,0,0,0,0,0
DATA 0,1,0,0,0,0,1
DATA 1,1,1,1,1,1,1
DATA 0,1,0,0,0,0,1
DATA 0,0,0,0,0,0,0
DATA 0,0,0,0,0,0,0
DATA 1,1,1,1,0,1,1
DATA 1,0,0,1,0,0,1
DATA 1,0,0,1,0,0,1
DATA 1,0,0,1,0,0,1
DATA 1,1,1,1,1,1,1
DATA 0,0,0,0,0,0,0
DATA 1,1,1,1,0,1,1
DATA 1,0,0,1,0,0,1
DATA 1,0,0,1,0,0,1
DATA 1,0,0,1,0,0,1
DATA 1,1,1,1,1,1,1
MAT READ G
PRINT "初期パターン"
FOR IX=1 TO AX
FOR IY=1 TO AY
IF G(AX*(IY-1)+IX)=1 THEN PRINT "■"; ELSE PRINT "□";
NEXT IY
PRINT
NEXT IX
PRINT
REM 初期パターンを基本配列に戻す
FOR J=1 TO DM
LET B(DM+1,J)=G(J)
NEXT J
FOR J=DM TO AX+1 STEP -1
IF B(DM+1,J)=1 THEN
LET IX2=J-AX
CALL addbec(B,DM+1,IX2)
LET PR(AX+1,IX2)=MOD(PR(AX+1,IX2)+1,2)
END IF
NEXT J
MAT BFC=BF
FOR J=AX TO 1 STEP -1
FOR K=1 TO AX
IF BFC(K)=1 AND B(DM-AX+K,J)=1 THEN
LET BFC(K)=0
IF B(DM+1,J)=1 THEN
CALL addbec(B,DM+1,DM-AX+K)
CALL addbec(PR,AX+1,K)
EXIT FOR
END IF
END IF
NEXT K
NEXT J
PRINT "剰余ビット :";
FOR J=1 TO 4
PRINT B(DM+1,J);
NEXT J
PRINT
PRINT
PRINT "基本配列へ戻すためのボタン配列"
FOR J=0 TO 2^(AX-ID)-1
CALL addbec(PR,AX+2,AX+1)
LET ADC=J
FOR K=1 TO AX
IF BF(K)=0 THEN
IF MOD(ADC,2)=1 THEN CALL addbec(PR,AX+2,K)
LET ADC=INT(ADC/2)
END IF
NEXT K
LET PCT=0
FOR K=1 TO DM
IF PR(AX+2,K)=1 THEN LET PCT=PCT+1
NEXT K
PRINT "PATTERN No : ";J+1
PRINT "手数 : ";PCT
CALL outpat
PRINT
CALL addbec(PR,AX+2,AX+2)
NEXT J
SUB becset
MAT B=ZER
LET BRW=0
FOR K=1 TO AY
FOR J=1 TO AX
LET BRW=BRW+1
FOR L=1 TO 5
LET IX=J+DR(L,1)
LET IY=K+DR(L,2)
IF IX>=1 AND IX<=AX AND IY>=1 AND IY<=AY THEN
LET BCL=(IY-1)*AX+IX
LET B(BRW,BCL)=1
END IF
NEXT L
NEXT J
NEXT K
END SUB
SUB prnarr
FOR J=1 TO DM
FOR K=1 TO DM
PRINT B(J,K);
NEXT K
PRINT
NEXT J
END SUB
SUB convbe
MAT PR=ZER
FOR J=1 TO AX
LET IX=DM-AX+J
LET IY=DM
LET PR(J,IX)=1
DO
IF B(IX,IY)=1 THEN
LET IX2=0
DO
LET IX2=IX2+1
IF IX2>DM THEN STOP
IF B(IX2,IY)=1 THEN
CALL addbec(B,IX,IX2)
LET PR(J,IX2)=1
EXIT DO
END IF
LOOP
END IF
LET IY=IY-1
LOOP UNTIL IY=AX
NEXT J
END SUB
SUB addbec(ARR(,),IX,IX2)
FOR L=1 TO DM
LET arr(IX,L)=MOD(ARR(IX,L)+ARR(IX2,L),2)
NEXT L
END SUB
SUB prnpro
FOR J=1 TO AX
PRINT "ベクトルNo : ";DM-AX+J
LET PCT=0
FOR K=1 TO DM
IF PR(J,K)=1 THEN
PRINT K;
LET PCT=PCT+1
IF MOD(PCT,10)=0 THEN PRINT
END IF
NEXT K
PRINT
PRINT "構成個数 : ";PCT
PRINT
NEXT J
END SUB
SUB prnrem
FOR J=DM-AX+1 TO DM
FOR K=1 TO AX
PRINT B(J,K);
NEXT K
PRINT
NEXT J
PRINT
END SUB
SUB caldim
MAT BF=ZER
LET BX=DM-AX
LET ID=0
FOR J=AX TO 1 STEP -1
LET SF=0
FOR K=1 TO AX
IF B(BX+K,J)=1 THEN
IF SF=0 AND BF(K)=0 THEN
LET SF=1
LET IK=K
LET BF(K)=1
LET ID=ID+1
ELSEIF BF(K)=0 THEN
CALL addbec(B,BX+K,BX+IK)
CALL addbec(PR,K,IK)
END IF
END IF
NEXT K
NEXT J
END SUB
SUB outpat
FOR IX=1 TO AX
FOR IY=1 TO AY
IF PR(AX+2,AX*(IY-1)+IX)=1 THEN PRINT "■"; ELSE PRINT "□";
NEXT IY
PRINT
NEXT IX
END SUB
END
【問題2】
同じプログラムで剰余ビットを求めると、0,1,1,0(ビット1〜4)となり、解がないことがわかります。
剰余ビットを0とするため、別に、ビット毎に剰余ビットを求め、同じ剰余になるものを探しました。
1ビットのみでは適合するものは存在せず、2ビットの剰余の排他的論理和で条件に合ったものを作ることができます。
例として、(2,1)、(1,13)をオンとした下記パターンが適合します。
□■■■□□□■■■□□■■■■□ ■■□□■□■□□□■□■□□□■ □□□□■□■□□□■□■□□□■ □□□■□□■□□□■□■□□□■ □□■□□□■□□□■□■□□□■ □■□□□□■□□□■□■□□□■ ■■■■■□□■■■□□□■■■□【おまけ】
4個の従属なベクトルのグループは以下の通りです。
ベクトルNo : 116 2 4 6 8 9 11 13 14 16 20 24 25 26 32 46 52 53 54 58 62 64 65 67 69 70 72 74 76 86 88 90 92 93 95 97 98 100 104 108 109 110 116 構成個数 : 42 ベクトルNo : 117 1 7 8 9 13 14 15 17 19 21 23 24 26 27 31 33 45 47 51 52 54 55 57 59 61 63 64 65 69 70 71 77 85 91 92 93 97 98 99 101 103 105 107 108 110 111 115 117 構成個数 : 48 ベクトルNo : 118 2 6 8 9 10 12 13 14 22 23 24 26 27 28 30 34 44 48 50 51 52 54 55 56 64 65 66 68 69 70 72 76 86 90 92 93 94 96 97 98 106 107 108 110 111 112 114 118 構成個数 : 48 ベクトルNo : 119 3 5 9 10 12 13 15 17 19 21 22 23 27 28 29 35 43 49 50 51 55 56 57 59 61 63 65 66 68 69 73 75 87 89 93 94 96 97 99 101 103 105 106 107 111 112 113 119 構成個数 : 48全体をまとめると以下のようになります。
従属ベクトルのグループ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 構成個数 : 102 独立ベクトルのグループ 18 36 37 38 39 40 41 42 60 78 79 80 81 82 83 84 102 構成個数 : 17基本図に戻すのに一番手数のかかる配置は、以上の従属のグループのどのような組み合わせでも、ベクトルの半分が選択されるように ベクトルを選択することにより求められます。
上記4つのグループにより分割される15種のサブグループ内のベクトルは、求めてみると、すべて0もしくは偶数個になっていますので
丁度1/2ずつ選択することができます。
例として以下のような選択があります。
ボタンの指定 ■■■■■■■■■□□■□□□□□ ■■■■■■■■■■■■□□□□□ ■■■■■■■■■□□■□□□□□ ■■■■■■■■■□□■□□■□□ ■■■■■■■■□□□■□□□□□ ■■■■■■□□□□□■□□□□□ ■■■■■■■■□□□■□□□□□ボタン数 : 68
この選択により生成されるパターンは下記のとおりです。
■□□□□□□□■□□□■□□□□ □■■■■■■■■■■□■□□□□ □■■■■■■■□□□■■□■□□ □■■■■■■■■■■■■■■■□ □■■■■■□■□□■■■□■□□ □■■■■□■□□□■■■□□□□ ■□□□□□■□■□■□■□□□□このパターンはPush数68で基本図に戻ります。
◆愛知県 Y.M.Ojisan さんからの解答。
【問題1】 50回
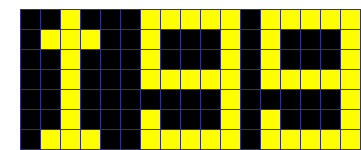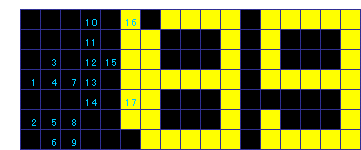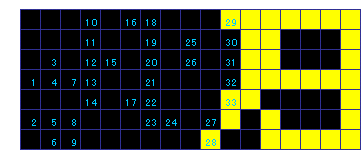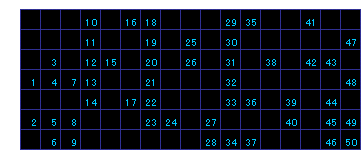
図中青い数字はプッシュの順番号です。
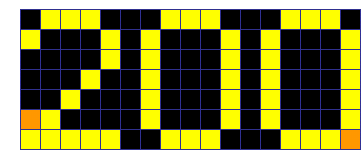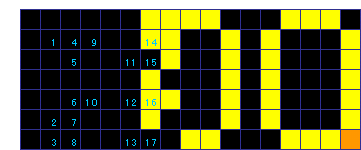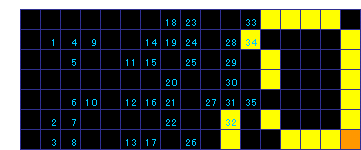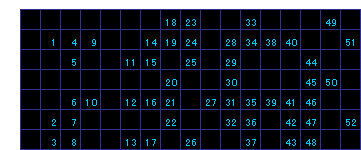
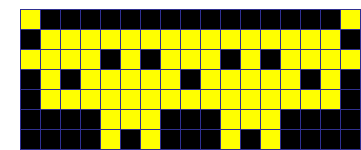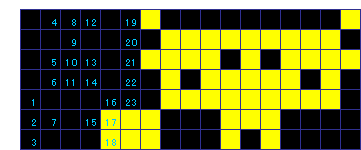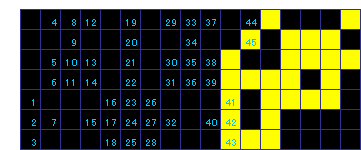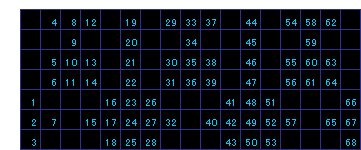
【問題2】 下図■2個追加 52回
【おまけ】 68回
例えば下記のパターンが存在しています。
本結果はPCプログラムによるもので、プッシュ数極大化+モンテカルロ法を行っています。
多数解があるので容易に何らかの解に達します。

証明と機械的作り方
まず、基本図を基本図に戻すプッシュパターンを考えます。
1列目のプッシュパターンを決めると2列目以降は必然的に決まります。
従って、プッシュなしを含む128パターンを調べればよく、その結果その内16パターンが基本図を基本図に戻すパタ−ンであることがわかりました。
これらは下記4次元の単位パターンの組み合わせ(排他論理和)で表すことが可能です。
| 1 | 2 |
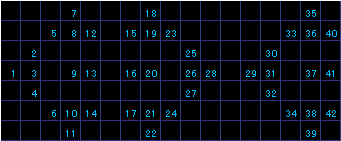 |
 |
| 22 | 23 |
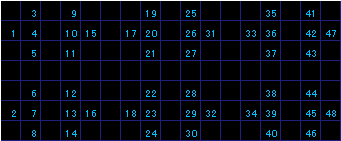 |
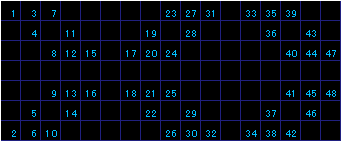 |
そして、プッシュを1としてこれら4パターンを2進法的に足し合わせると、下記のパターンが得られます。
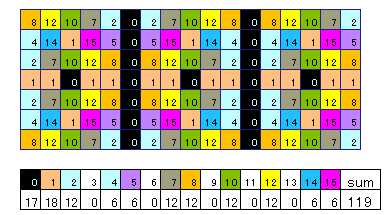
119=7×17
値が「0」のところは17ヶ所あり、これらの位置はプッシュしておけば常にプッシュすべき位置となります。
他の位置は必ず全部パターンの半分のパターンでプッシュされます。
よって、24=16個のパターンを作用させた後のプッシュパターン合計のプッシュ数平均値は
17+(119−17)×0.5=68 です。
つまり、68より多いプッシュパターンがあるときは68未満のプッシュパターンもあることになり、68が最大であることがわかります。
次に作り方ですが、「0」以外のところは都合よく全て偶数個ずつあります。
従って、おのおのその半分の個数の位置を適当にプッシュすべき位置とすれば、プッシュ数がパターンにより変わることはなく全部68回となります。
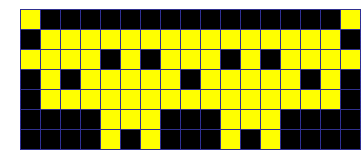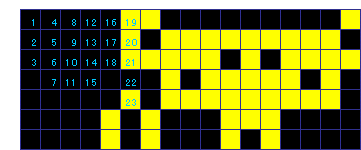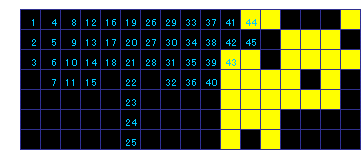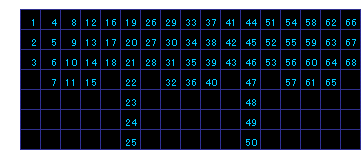
下に示す例は、プッシュ位置が可能な限り上半分に在るプッシュパターンから得た初期状態です。
上図は、そのプッシュパターンで操作したもの、下図は別のプッシュパターンで操作したもので、いずれも68回です。
◆ 問題へもどる
◆ 今週の問題へ