
仧峀搰導丂惔愳丂堢抝 偝傫偐傜偺夝摎
亂栤戣侾亃
12+22+32+42=30(屄)
亂栤戣俀亃
9杮
丂乕丂丂丂乕丂乕 乥丂乥丂乥丂丂丂乥 丂丂丂乕丂乕丂乕 乥丂乥丂丂丂乥丂乥 丂乕丂乕丂乕丂丂 乥丂丂丂丂丂乥丂乥 丂乕丂乕丂乕丂乕 乥丂丂丂乥丂丂丂乥 丂乕丂乕丂乕丂乕亂栤戣俁亃
亂栤戣俁亅侾亃
2*n*(n+1) 杮
亂栤戣俁亅俀亃
12+22+丒丒丒丒+n2=n*(n+1)*(2*n+1)/6(屄)
亂偍傑偗侾亃
4*4 1) 丂乕丂丂丂乕丂乕 乥丂乥丂乥丂丂丂乥 丂丂丂乕丂乕丂乕 乥丂乥丂丂丂乥丂乥 丂乕丂乕丂乕丂丂 乥丂丂丂丂丂乥丂乥 丂乕丂乕丂乕丂乕 乥丂丂丂乥丂丂丂乥 丂乕丂乕丂乕丂乕 2) 丂乕丂丂丂乕丂乕 乥丂乥丂乥丂乥丂乥 丂丂丂乕丂丂丂丂 乥丂乥丂乥丂乥丂乥 丂乕丂丂丂丂丂乕 乥丂乥丂乥丂乥丂乥 丂丂丂乕丂乕丂丂 乥丂乥丂丂丂乥丂乥 丂乕丂乕丂乕丂乕夞揮丄棤曉偟偱摨偠偵側傞傕傪侾捠傝偲偡傞偲丄俀捠傝丅
1 2 3 4
5 6 7 8 9
10 11 12 13
14 15 16 17 18
19 20 21 22
23 24 25 26 27
28 29 30 31
32 33 34 35 36
37 38 39 40
1) 2 8 10 16 22 24 25 33 35
2) 2 10 12 13 20 21 28 31 34
3) 3 6 13 16 19 25 26 33 35
4) 3 10 11 13 20 21 28 31 34
5) 6 8 14 16 22 24 25 33 35
6) 6 8 15 16 22 23 25 33 35
7) 6 8 15 16 22 25 28 35 38
8) 6 8 16 17 19 25 27 33 35
9) 6 8 16 17 19 25 31 33 39
10) 6 8 16 18 19 25 26 33 35
11) 6 12 13 14 20 21 28 31 34
12) 7 10 13 20 21 23 30 31 33
13) 7 10 13 20 21 27 28 29 35
14) 7 10 13 20 21 28 29 31 39
15) 7 10 13 20 21 28 30 31 38
16) 8 10 11 18 20 21 28 31 34
16捠傝丅乮屌掕偟偰乯
亂偍傑偗俀亃
仠5亊5偵暲傋偨応崌
丂乕丂乕丂 丂乕 乕 乥丂 丂乥丂乥丂 丂乥 丂乕丂乕丂乕丂 乕 乥丂乥丂 丂乥丂乥丂乥丂 丂 乕丂乕丂乕 乥丂乥丂乥丂 丂乥丂乥丂 丂乕丂 丂乕丂乕 乕 乥丂乥丂乥丂 丂 丂乥丂 丂 丂乕丂乕丂乕 乕 乥丂乥丂 丂乥丂 丂乥 乕丂乕丂乕丂乕 乕14杮
仠6*6
丂乕丂 丂乕丂乕丂乕丂乕
乥丂乥 乥丂乥丂 丂乥 乥
丂 丂乕丂 丂乕 乕
乥丂乥丂乥 乥丂乥丂乥丂乥
丂乕丂 丂乕 丂 丂乕
乥丂乥丂乥丂乥丂乥丂乥丂乥
丂 丂乕 丂 乕
乥丂乥丂乥丂乥丂乥 乥丂乥丂
丂乕 丂乕丂乕丂 乕
乥丂乥丂乥 丂乥丂乥丂乥
丂乕丂乕丂乕 乕
乥丂乥丂 乥丂 丂乥丂乥
乕丂乕丂乕丂乕 乕 乕19杮仠7*7(3*3,5*5)
丂乕丂乕 乕丂乕丂乕丂乕丂乕
乥丂乥 丂乥丂 丂乥 乥
丂 乕丂乕丂乕 乕丂乕 乕
乥丂乥丂乥 丂乥丂 丂乥
丂乕丂 乕 乕丂乕 乕 乕
乥丂乥丂乥丂乥丂 丂乥丂 乥
丂 乕 丂乕 乕 乕丂乕
乥丂乥丂乥丂 丂乥 丂乥丂乥
丂乕 乕丂乕丂乕丂乕
乥丂乥丂乥 乥丂乥丂乥
乕 乕 乕丂乕丂 乕
乥丂乥丂 乥 丂乥丂乥丂乥
乕丂乕丂乕丂乕 乕 乕
乥丂 丂乥丂 丂乥 丂乥 乥
乕丂乕丂乕丂乕 乕 乕 乕仠8*8(2*2,4*4,6*6)
丂乕丂乕 乕丂乕丂乕丂乕丂乕 乕
乥丂 乥丂 丂乥丂 乥 乥
丂乕 乕丂乕丂乕 乕丂乕 乕 乕
乥丂乥丂 乥丂 丂乥丂 乥
丂 丂乕 乕 乕丂乕 乕 乕 乕
乥丂乥丂乥丂 丂乥丂 丂乥 乥
丂乕 乕丂乕 乕 乕丂乕 乕
乥丂乥丂乥丂乥丂 乥丂 丂乥 乥
丂 乕 丂乕丂乕丂乕 乕
乥丂乥丂乥 乥 丂乥丂乥 乥
乕 乕 乕丂乕丂乕 乕
乥丂乥丂乥 乥丂 丂乥丂乥 乥
丂乕丂乕丂乕 乕 乕 乕
乥丂乥丂 丂乥丂 乥丂 乥 乥
乕丂乕丂乕丂乕 乕 乕 乕 乕
乥丂 丂乥丂 丂乥 丂乥 乥
乕丂乕丂乕丂乕 乕 乕 乕 乕拞墰偐傜尒傞偲曪娷偝傟偰偄傞偺偑敾傝傑偡丅
仠n*n
F(n)=Ceiing(n2/2)+1
n亞2丄F(1)=1
仧峀搰導偺拞妛峑俀擭惗丂CHEMI 偝傫偐傜偺夝摎
亂栤戣侾亃
儅僢僠朹堦杮偺挿偝傪侾偲偟傑偡丅
偙偺偲偒丄栤戣恾偺拞偵偼丄堦曈偑侾偺惓曽宍偐傜嵟戝係偺惓曽宍傑偱偁傝傑偡丅
偙偙偱丄偦傟偧傟偺戝偒偝偺惓曽宍偺悢偼丄
乽忋壓偵偢傜偣傞悢乿亊乽嵍塃偵偢傜偣傞悢乿
側偺偱丄
仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏 堦曈偺挿偝乥丂丂寁嶼丂丂乥摎偊 乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗 丂丂侾丂丂乥係亊係亖侾俇乥侾俇 丂丂俀丂丂乥俁亊俁亖丂俋乥丂俋 丂丂俁丂丂乥俀亊俀亖丂係乥丂係 丂丂係丂丂乥侾亊侾亖丂侾乥丂侾 乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗 丂丂丂丂丂丂丂丂丂丂崌寁乥俁侽 仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏傛偭偰俁侽屄丅
亂栤戣俀亃
堦曈侾偺惓曽宍偼侾俇屄偁傝傑偡丅
懠偼丄偦傟傜傪徚偡偲偒偵堦弿偵徚偣偽偄偄偱偟傚偆丅
傛偭偰丄偦傟傜傪徚偡偺偵偼俉杮徚偣偽偄偄偙偲偵側傝傑偡丅
偟偐偟丄
丂乗丂乗 乥丂丂丂乥 丂乗丂乗偱杽傔傞偲丄堦曈偑俀偺惓曽宍傪偡傋偰徚偡偙偲偑偱偒傑偣傫丅
傑偨丄俉杮偱徚偦偆偲偡傞偲丄堦曈偑係偺惓曽宍傪徚偡偙偲偑偱偒傑偣傫丅
偩偐傜丄俉杮偱丄堦曈偑侾偺惓曽宍堦屄偲堦曈偑係偺惓曽宍傪彍偔偡傋偰偺惓曽宍傪徚偟偰丄傕偆堦杮徚偟偰巆傝偺擇偮偺惓曽宍傪摨帪偵徚偟傑偡丅
嵶偐偄徹柧偼偟傑偣傫偑乮偭偰偄偆偐偱偒傑偣傫乯姶妎揑偵偙傟側傜偆傑偔偄偔偲傢偐傝傑偡丅
傛偭偰丄俋杮徚偡昁梫偑偁傝傑偡丅
-椺-
丂乕丂乕丂丂丂乕 乥丂乥丂乥丂乥丂乥 丂丂丂丂丂乕丂丂 乥丂乥丂乥丂乥丂乥 丂乕丂丂丂丂丂乕 乥丂乥丂乥丂乥丂乥 丂丂丂乕丂乕丂丂 乥丂乥丂丂丂乥丂乥 丂乕丂乕丂乕丂乕亂栤戣俁亅侾亃
n亊n偐傜(n+1)亊(n+1)偵偡傞偲偒偵丄傑偢曈傪侾偢偮怢偽偝側偗傟偽偄偗傑偣傫丅
偦偺偨傔偵偼{2亊(n+1)}杮昁梫偱偡丅
偦偟偰丄塃抂偺曈偲壓偺曈傪嶌傞偵偼丄{2亊(n+1)}杮昁梫偱偡丅
埲忋偺偙偲偐傜丄杔偼師偺傛偆側斀暅幃傪嶌傝傑偟偨丅
仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏 倃1 亖 係丂 丂(堦曈偑侾偺惓曽宍傪嶌傞偺偵昁梫側儅僢僠朹偺杮悢) 倃m+1 亖 倃m 亄 係 亊 (倣 亄 侾) 仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏仏倃n偑乮値亊値乯偺惓曽宍傪嶌傞偲偒偵昁梫側儅僢僠朹偺杮悢偱偡丅
亂栤戣俁亅俀亃
偙傟偼丄亂栤戣侾亃偺峫偊曽傪巊偆偲丄
| n 嚁 k=1 |
k2偩偲傢偐傝傑偡丅 |
亂偍傑偗俀亃
偙傟偼丄亂栤戣俀亃偺峫偊曽傪巊偆偲丄
n2/2+1
偲側傝傑偡偑丄値偑婏悢偺偲偒偵彫悢揰偑偱傑偡丅
偙偺偲偒丄愗傝幪偰傞偲偡傋偰徚偡偙偲偑偱偒側偄偺偱乮彮側偔側傞偐傜乯丄彫悢揰埲壓偼愗傝忋偘偨傕偺偑摎偊偲側傝傑偡丅
仧愮梩導丂嵷壴巕 偝傫偐傜偺夝摎

仧惷壀導丂medaka 偝傫偐傜偺夝摎
亂栤戣侾亃丂俁侽屄
亂栤戣俀亃
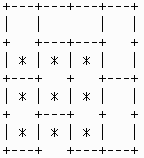
(峫偊曽乯
俁倶俁偺摎偊(*偺晹暘乯傪傕偲偵忋懁偲塃懁偺晹暘傪奼挘偟偨
亂栤戣俁亅侾亃
(摎偊乯
儅僢僠朹偺悢傪俴乮値乯偲偡傞偲
俴乮値乯亖俀仏値仏乮値亄侾乯
(媮傔曽乯
俴乮侾乯亖丂係
兟俴乮値乯亖丂俴乮値乯亅俴乮値亅侾乯偲偡傞偲丄兟俴乮値乯亖係仏値偲側傞丅
偙傟傛傝丄俴乮値乯亖儼兟俴乮倠乯偲偟偰丄忋婰偺摎偊傪摼傞丅
倕倶丏俴乮係乯亖俀仏係仏乮係亄侾乯亖係侽
亂栤戣俁亅俀亃
(摎偊乯丂惓曽宍偺屄悢傪俽乮値乯偲偡傞偲
| 俽乮値乯亖 | 値仏乮値亄侾乯仏乮俀仏値亄侾乯 俇 |
乮媮傔曽乯
倣倶倣偺惓曽宍偼丄墶曽岦偵乮値亅倣亄侾乯屄丄廲曽岦偵傕乮値亅倣亄侾乯屄傪攝抲偱偒傞偺偱
慡懱偱偼丄乮値亅倣亄侾乯2屄偑懚嵼偡傞丅廬偭偰丄
丂俽乮値乯
亖値2亄乮値乕侾乯2亄乮値乕俀乯2亄丏丏丏亄侾2
亖丂儼倠2
亖丂儼乷倠仏乮倠亅侾乯亄倠乸
| 亖 | 値仏乮値亄侾乯乮値亅侾乯 俁 | 亄 | 値仏乮値亄侾乯 俀 |
| 亖 | 値仏乮値亄侾乯仏乮俀仏値亄侾乯 俇 |
亂偍傑偗侾亃
乮摎偊乯
埲壓偺俀屄丅
偨偩偟丄懳徧夝傪暿暔偲偟偰悢偊傞応崌偼丄侾俇屄丅
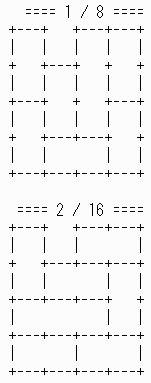
亂栤戣俀亃偺夝偼丄嵟弶偺夝傪忋壓斀揮偟偨傕偺偵堦抳偟偰偄傞丅
値亖俆偺応崌偼丄俋侾屄丅
偨偩偟丄懳徧夝傪暿暔偲偟偰悢偊傞応崌偼丄俈俀侽屄丅
乮媮傔曽乯
僾儘僌儔儉(嵟屻偵揧晅乯偵傛傞扵嶕偱媮傔偨丅
(僾儘僌儔儉偺愢柧偼妱垽)
亂偍傑偗俀亃
乮摎偊乯丂庢傝彍偔儅僢僠朹偺嵟彫悢傪倣乮値乯偲偡傞偲
| 倣乮値乯亖乵 | 値2亄侾 俀 | 乶亄侾 |
偨偩偟丄乵倎乶偼僈僂僗婰崋偱丄倎偺惍悢晹暘傪昞偡丅
乮倕倶丏乵俁乶亖俁丆乵俁丏俆乶亖俁乯
| 値 | 倣乮値乯 |
| 俁 | 俇 |
| 係 | 俋 |
| 俆 | 侾係 |
| 俇 | 侾俋 |
| 俈 | 俀俇 |
乮媮傔曽乯
値亖俁偼丄柧傜偐乮亀惓曽宍偺徚柵亁嶲徠乯偱偁傞偺偱丄値亞係偵偮偄偰挷傋傞偙偲偵偡傞丅
侾乯庢傝彍偔儅僢僠朹偺悢偑倣乮値乯偲側傞傛偆側夝偑懚嵼偡傞偙偲傪埲壓偵帵偡丅
値亖係偼丄亂栤戣俀亃偱柧傜偐偱偁傞丅
値亜係偵偮偄偰偼丄係倶係偺夝傪儀乕僗偲偟偰埲壓偺庤弴偱嶌傞偙偲偑偱偒傞丅
値偑嬼悢偺偲偒丄値倶値偐傜乮値亄侾乯倶乮値亄侾乯偺夝傪嶌傞庤弴
倎乯値倶値偺忋懁偵嵍偐傜塃傊偲侾倶俀偺挿曽宍傪暲傋傞
倐乯値倶値偺塃懁偵忋偐傜壓傊偲俀倶侾偺挿曽宍傪暲傋傞
們乯塃壓偺侾倶侾偺惓曽宍偺椞堟偼丄壓偺晹暘傪奐偗偨傑傑偵偡傞
値偑婏悢偺偲偒丄値倶値偐傜乮値亄侾乯倶乮値亄侾乯偺夝傪嶌傞庤弴
倓乯値倶値偺嵍懁偵忋偐傜壓傊偲俀倶侾偺挿曽宍傪暲傋傞丅
倕乯値倶値偺壓懁偵偁傞侾倶侾偺惓曽宍乮壓偑奐偄偰偄傞乯偼丄俀倶侾偺挿曽宍偵偡傞
倖乯倕乯偱嶌傜傟偨挿曽宍偱偼偝傑傟偨晹暘傪侾倶俀偺挿曽宍偱偆傔傞
倗乯倓乯丆倕乯偵偼偝傑傟偨侾倶侾偺惓曽宍偺椞堟偼丄壓偺晹暘傪奐偗偨傑傑偵偡傞
忋婰偺庤弴倎乯乣倗乯偵傛傝丄値亖係偐傜弴偵値亖俆乣俉傪嶌惉偡傞椺傪帵偡丅
![]() 偼丄庤弴倎乯偺憖嶌偱嶌傜傟偨偙偲傪昞偡丅
偼丄庤弴倎乯偺憖嶌偱嶌傜傟偨偙偲傪昞偡丅
乮倐乣倗傕摨條乯
値亖係偺応崌乮儀乕僗夝乯
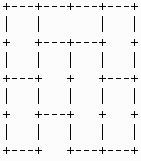
値亖俆偺応崌
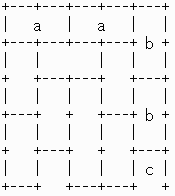
値亖俇偺応崌
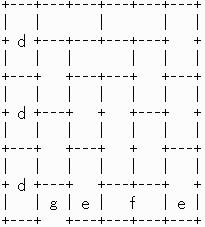
値亖俈偺応崌
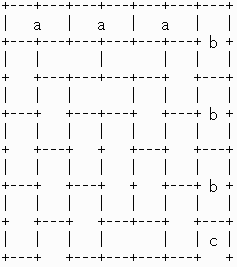
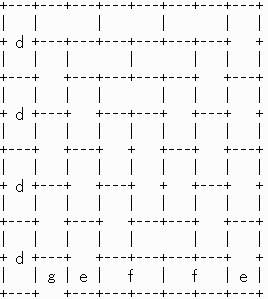
値亖俉偺応崌
俀乯夝偑懚嵼偡傞偨傔偺,昁梫忦審
倢乮値乯傪埲壓偺傛偆偵掕媊偡傞偲丄夝偑懚嵼偡傞偨傔偵偼丄
庢傝彍偔儅僢僠朹偺悢亞倢乮値乯傪枮偨偡偙偲偑昁梫偱偁傞丅
| 倢乮値乯亖乵 | 値2 俀 | 乶亄侾 |
偨偩偟丄乵倠乶偼僈僂僗婰崋偱丄倠偺惍悢晹暘傪昞偡丅
侾倶侾偺惓曽宍偼値2屄懚嵼偡傞丅
偙偺惓曽宍傪傕偭偲傕彮側偄悢偺儅僢僠朹偱徚柵偝偣傞偵偼丄俀偮偺侾倶侾偺惓曽宍偺娫偺侾杮傪庢傝彍偄偰丄侾倶俀 or 俀倶侾偺挿曽宍傪嶌傞偙偲偱偁傞丅
値2屄偺惓曽宍傪偙偺曽朄偱峴偆偲偡傞偲丄
| 乵 | 値2 俀 | 乶杮偺儅僢僠朹偑昁梫偱偁傞丅 |
堦曽丄偙偺曽朄偱偼丄値倶値偺惓曽宍偼徚柵偟側偄偺偱丄偙傟傪徚柵偝偣傞偨傔偵丄傕偆1杮偺儅僢僠朹偑昁梫偲側傞丅
| 廬偭偰丄乵 | 値2 俀 | 乶亄侾亖倢乮値乯偑昁梫偱偁傞丅 |
値偑婏悢偺応崌丄侾倶侾偺惓曽宍偑侾偮巆傞偑丄偙偺惓曽宍偼丄値倶値偺惓曽宍偲曈傪嫟桳偟偰偄傟偽丄値倶値偺惓曽宍傪徚柵偝偣傞帪偵丄摨帪偵徚柵偝偣傞偙偲偑偱偒傞丅
廬偭偰丄値偑婏悢偺応崌傕丄
| 乵 | 値2 俀 | 乶亄侾亖倢乮値乯杮偺儅僢僠朹偑昁梫忦審偲側傞丅 |
俁乯師偵丄倣乮値乯偑嵟彫夝偱偁傞偙偲傪帵偡丅
| 値偑嬼悢偺応崌丄乵 | 値2亄侾 俀 | 乶亖乵 | 値2 俀 | 乶偲側傝丄 |
値偑婏悢偺応崌丄倣乮値乯亖倢乮値乯亄侾偑惉傝棫偮丅
傕偟丄倢乮値乯偲側傞夝偑懚嵼偟側偗傟偽丄倣乮値乯偑嵟彫夝偲偄偊傞丅
仠曗戣侾
壓恾偺傛偆偵丄侾倶俀偺挿曽宍俙偺椉懁傪僈乕僪偝傟偨忬懺偱丄倶丆倷偺埵抲傪侾倶俀偲俀倶侾偺挿曽宍偩偗偱杽傔傞偙偲偼偱偒側偄丅
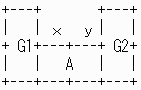
俧侾丆俧俀偼丄俀倶侾偺挿曽宍枖偼抂
佹丂倶丄倷傪杽傔傛偆偲偡傞偲丄偳偆偟偰傕俀倶俀偺惓曽宍偑偱偒偰偟傑偆丅
仠曗戣俀
壓恾偺傛偆偵丄侾倶俀偺挿曽宍偑倠屄暲傫偩椉懁傪僈乕僪偝傟偨忬懺偱丄
倶侾丏丏丏倶俀倠偺埵抲傪侾倶俀偲俀倶侾偺挿曽宍偩偗偱杽傔傞応崌丄
侾倶俀偺挿曽宍偼丄崅乆乮倠亅侾乯屄偟偐暲傋傞偙偲偑偱偒側偄丅
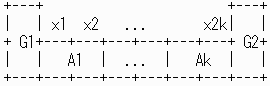
俧侾丆俧俀偼丄俀倶侾偺挿曽宍枖偼抂
倶侾丆倶俀倠偺埵抲偼丄俀倶侾偺挿曽宍傪攝抲偟側偗傟偽側傜側偄偺偱丄巆傝傪侾倶俀偺挿曽宍偱杽傔偨偲偟偰傕崅乆乮倠亅侾乯屄偲側傞丅
曗戣侾丆俀傪巊偭偰丄倢乮値乯偲側傞夝偑懚嵼偟側偄偙偲傪帵偡丅
傕偟丄倢乮値乯偺夝偑懚嵼偡傞偲壖掕偡傞偲丄侾倶侾偺惓曽宍偑値倶値偺惓曽宍偲曈傪嫟桳偟丄偦偺曈偼庢傝彍偐傟偰偄傞丅
巆傝偺乮値2亅侾乯屄偺侾倶侾偺惓曽宍偼丄俀偮偑崌傢偝偭偰侾倶俀 or俀倶侾偺挿曽宍偲側偭偰偄側偗傟偽側傜側偄丅
乮倢乮値乯偺崁偱弎傋偨偙偲乯
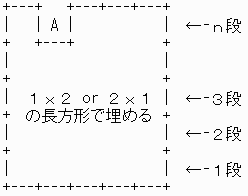
忋恾偺傛偆偵丄侾抜丄俀抜丄丏丏丏丄値抜偲弴偵侾倶俀倧倰俀倶侾偺挿曽宍傪杽傔偰偄偔偙偲偵偡傞丅
側偍丄侾倶侾偺惓曽宍俙偼嵟忋抜偵攝抲偡傞偙偲偵偡傞丅
(偙偆偟偰傕堦斒惈偼幐傢傟側偄乯
値偼婏悢側偺偱丄値亖乮俀仏倠亄侾乯偲偡傞偲丄侾抜栚偵偼嵟戝偱倠屄偺侾倶俀偺挿曽宍傪攝抲偡傞偙偲偑偱偒傞丅
侾抜栚偵倠屄傪攝抲偟偨応崌丄曗戣俀偵傛傝丄俀抜栚偼丄崅乆乮倠亅侾乯屄偺侾倶俀偺挿曽宍偟偐攝抲偱偒側偄丅
偙傟傪孞傝曉偟偰偄偔偲丄倠抜栚偱曗戣侾偺忬懺偲側傝丄偙傟埲忋偼攝抲偱偒側偔側傞丅
乮懄偪丄夝偑懚嵼偟側偄乯
傕偟丄搑拞偱丄侾倶俀偺挿曽宍偺悢傪彮側偔攝抲偟偨応崌偼丄傕偭偲彮側偄抜悢偱曗戣侾偺忬懺偲側傞丅
椺丂俆倶俆偺応崌
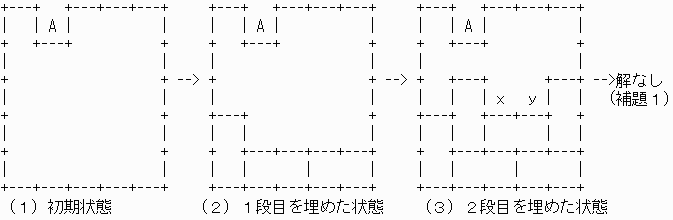
埲忋傛傝丄侾倶俀偺挿曽宍偼丄崅乆倠抜傑偱偟偨愊傒忋偘傞偙偲偑偱偒側偄偺偱丄夝偼懚嵼偟側偄丅
廬偭偰丄値偑婏悢偺応崌丄倢乮値乯偲側傞夝偼懚嵼偟側偄偺偱丄倣乮値乯偑嵟彫夝偱偁傞丅
<<偍傑偗俀偺僒儅儕>>
彮偟挿偔側偭偨偺偱丄埲忋偺榑巪傪傑偲傔傞偲
侾乯庢傝彍偔儅僢僠朹偺悢偑倣乮値乯偲側傞傛偆側夝偑懚嵼偡傞丅
俀乯夝偑懚嵼偡傞偨傔偵偼丄庢傝彍偔儅僢僠朹偺悢亞倢乮値乯傪枮偨偡偙偲偑昁梫偱偁傞丅
俁乯値偑嬼悢偺応崌丄倣乮値乯亖倢乮値乯偑惉棫偡傞偺偱丄倣乮値乯偼嵟彫夝偱偁傞丅
値偑婏悢偺応崌丄倣乮値乯亖倢乮値乯亄侾偑惉傝棫偮丅
偟偐偟丄倢乮値乯偲側傞夝偑懚嵼偟側偄偙偲偑帵偝傟偨偺偱丄倣乮値乯偑嵟彫夝偲側傞丅
亂偍傑偗侾亃偺扵嶕僾儘僌儔儉
##### 20004.06.06
#
#
import time
def exe(N) :
global AnsCount,DupCount,out
out = open("s%d-log.txt" % N,"w")
Init(N)
L = 2 * N * (N+1)
S = [0]
for m in range(1,N+1) :
mask = 0L
for k in range(0,L) : mask |= M[m][k]
S += [mask]
AnsCount = 0
DupCount = 0
maxdepth = (N*N + 1) / 2 + 1
OuterSearch(maxdepth,0,-1,[],S,N)
out.close()
##
def OuterSearch(MaxDepth,nest,Pos,PosList,S,N) :
if nest == 0 :
for p in range(0,(N+1)/2) :
Line = ("\n=== Search pos:%d Started === : " % (p)) + time.ctime()
WriteLog(out,Line)
SS = [0]
for m in range(1,N+1) : SS += [ (S[m] | M[m][p]) ^ M[m][p] ]
InnerSearch(MaxDepth,nest+1,-1,[p],SS,N)
OuterSearch(MaxDepth,nest+1,p,[p],SS,N)
Line = "\n=== Search Ended === : " + time.ctime()
WriteLog(out,Line)
return
if MaxDepth < ((N*N - nest) / 2 + nest + 1) : return
for pi in range(Pos+1,len(OutPos)) :
p = OutPos[pi]
poslist = PosList + [p]
if DupCheck(poslist,N) < 0 : continue
SS = [0]
for m in range(1,N+1) : SS += [ (S[m] | M[m][p]) ^ M[m][p] ]
InnerSearch(MaxDepth,nest+1,-1,poslist,SS,N)
OuterSearch(MaxDepth,nest+1,pi,poslist,SS,N)
##
def InnerSearch(MaxDepth,nest,Pos,PosList,S,N) :
global AnsCount,DupCount
if nest == MaxDepth :
for m in range(1,N+1) :
if S[m] != 0 : return
cnt = DupCheck(PosList,N)
if cnt < 0 : return
AnsCount += 1
DupCount += cnt
ID = "\n ==== %d / %d ====" % (AnsCount,DupCount)
printFig(ID,PosList,N)
return
for pi in range(Pos+1,len(InPos)) :
p = InPos[pi]
poslist = PosList + [p]
SS = [0]
for m in range(1,N+1) : SS += [ (S[m] | M[m][p]) ^ M[m][p] ]
if (bitcount(SS[1])+1)/2 + nest >= MaxDepth : continue
InnerSearch(MaxDepth,nest+1,pi,poslist,SS,N)
##
def bitcount(Mask) :
w = Mask
c = 0
while w != 0 :
c += 1
w = w & (w-1)
return c
##
def DupCheck(PosList,N) :
NN = N * (N+1)
C = []
for t in range(0,8) :
Pmask = 0L
for p in PosList :
if p < NN :
i = p % N ; j = p / N
if t & 0x01 : i = N-1 - i
if t & 0x02 : j = N - j
q = i + j*N
if t & 0x04 : q += NN
else :
i = (p-NN) % N ; j = (p-NN) / N
if t & 0x02 : i = N-1 - i
if t & 0x01 : j = N - j
q = i + j*N + NN
if t & 0x04 : q -= NN
Pmask |= 1L << (NN+NN-q)
if t == 0 :
P = Pmask
C =[P]
else :
if (P & OutMask) < (Pmask & OutMask) : return -1
if (P & OutMask) == (Pmask & OutMask) :
if (P & InMask) < (Pmask & InMask) : return -1
if Pmask not in C : C += [Pmask]
return len(C)
##
def Init(N) :
global M,InPos,OutPos,InMask,OutMask
NN = N * (N+1)
M = [[]]
for m in range(1,N+1) :
mask = []
for k in range(0,2*NN) : mask += [0]
M += [mask]
for i in range(0,N) :
if i+m > N : break
for j in range(0,N) :
if j+m > N : break
p = i*N + j
q = p + m*N
r = i + NN + j*N
s = r + m*N
for k in range(0,m) :
a = p + k
b = q + k
c = r + k
d = s + k
M[m][a] |= 1L << p
M[m][b] |= 1L << p
M[m][c] |= 1L << p
M[m][d] |= 1L << p
Line= " m=%d p=%d (%d,%d,%d,%d)" % (m,p,a,b,c,d)
WriteLog(out,Line)
InPos = [] ; InMask = 0L
OutPos = [] ; OutMask = 0L
NN2 = 2 * NN
for p in range(0,NN2) :
if p < NN : i = p / N
else : i = (p-NN) / N
if (i == 0) | (i == N) : OutPos += [p] ; OutMask |= 1L << (NN2-p)
else : InPos += [p] ; InMask |= 1L << (NN2-p)
##
def printFig(ID,PosList,N) :
H = [] ; V = []
h = '+'; v = '|'
for k in range(0,N) :
h += '---+'
v += ' |'
for n in range(0,N+1) :
H += [h]
V += [v]
for p in PosList :
if p < N*(N+1) :
i = p % N
j = p / N
h = H[j]
h = h[:i*4+1] + ' ' + h[i*4+4:]
H[j] = h
else :
p = p - N*(N+1)
i = p % N
j = p / N
v = V[i]
v = v[:j*4] + ' ' + v[j*4+3:]
V[i] = v
WriteLog(out,ID)
for k in range(0,2*N+1):
if (k & 0x01) : WriteLog(out,' ' + V[k/2])
else : WriteLog(out,' ' + H[k/2])
###
def WriteLog(out,Line) :
print Line
out.write(Line+"\n")
out.flush()
仧搶嫗搒丂傐偙傌傫 偝傫偐傜偺夝摎
1亊1 偺惓曽宍傪乽扨埵惓曽宍乿丆n亊n 偺惓曽宍傪乽慡懱惓曽宍乿偲屇傇偙偲偵偡傞丅
傑偨丆挿偝 1 偺曈乮儅僢僠朹 1 杮偵懳墳乯傪扨埵曈偲屇傇丅
亂栤戣侾亃
壓婰亂栤戣俁亅俀亃偺夝偱丆n = 4 偲偡傟偽丆
4亊5亊9/6 亖30 屄
亂栤戣俀亃
壓婰亂偍傑偗侾亃偺恾偵偍偄偰丆愒揰慄偺埵抲偵偁傞 9 杮偺扨埵曈傪庢傝彍偔偲惓曽宍傪娷傑側偄傛偆偵偱偒傞丅
亂栤戣俁亅侾亃
堦偮偺扨埵惓曽宍偵偦偺忋曈偲嵍曈傪懳墳偝偣傞偲丆偦傟偼扨埵惓曽宍摨巑偺娫偱廳暋偟側偄丅
傑偨丆慡懱惓曽宍偺塃曈偲壓曈偵懏偡傞 2n 杮偺扨埵曈偵偼懳墳偡傞惓曽宍偑側偄丅
埲忋偐傜丆媮傔傞曈偺杮悢偼
2n2 + 2n = 2n(n+1) 杮丂偱偁傞丅
亂栤戣俁亅俀亃
1 曈偑 k (1亝k亝n) 偺惓曽宍偑丆
慡懱惓曽宍偺撪晹偱
嵍塃偵摦偗傞帺桼搙偼 n+1-k 偱偁傝丆
忋壓偵摦偗傞帺桼搙傕摨偠偔 n+1-k 偱偁傞偐傜丆
偙偺戝偒偝偺惓曽宍偼 (n+1-k)2 屄偁傞丅
偟偨偑偭偰丆慡晹偱
| n 嚁 k=1 | (n+1-k)2 = | n 嚁 k=1 | k2 = | n(n+1)(2n+1) 6 |
屄 |
偁傞丅
亂偍傑偗侾亃
夞揮偲棤曉偟偵傛偭偰廳側傜側偄夝偼壓恾偺 2 捠傝丅
偙傟埲奜偵側偄偙偲偼僔儔儈捵偟偵傛傝妋偐傔偨丅
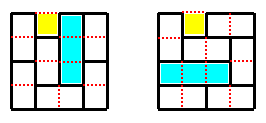
峫偊曽偼亂偍傑偗俀亃偵婰偡丅
亂偍傑偗俀亃
n亞3 偲偡傞丅
扨埵惓曽宍傪偡傋偰徚偡偨傔偵偼丆奺扨埵惓曽宍偐傜彮側偔偲傕 1 曈偢偮傪嶍彍偡傞昁梫偑偁傞偑丆
2 屄偢偮椬傝崌偆扨埵惓曽宍偺娫偺曈傪嶍彍偡傟偽丆1 曈偁偨傝 2 屄偢偮偺扨埵惓曽宍偑徚偊傞偙偲偵側傝丆
嶍彍杮悢偼嵟彫偱嵪傓丅
[1] n 偑嬼悢偺応崌偼丆偙傟偵傛偭偰 n2/2 枃偺僪儈僲曅乮2亊1 偺挿曽宍乯偑偱偒傞丅
偟偐偟丆偙偺僪儈僲曅傪揔摉偵攝抲偟偰慡懱惓曽宍傪杽傔偨偩偗偱偼丆慡懱惓曽宍偺曈偑嶍彍偝傟側偄傑傑巆偭偰偄傞偐傜丆
n2/2 杮傪嶍彍偟偨偩偗偱偼戣堄傪枮偨偡偙偲偼偱偒側偄丅
師偵丆扨埵曈傪 n2/2 + 1 杮嶍彍偡傞偙偲傪峫偊傞偲丆偙偺応崌偼幚嵺偵戣堄傪枮偨偡攝抲偑偁傞 (壓恾)丅
妋偐偵偙偺応崌丆僪儈僲曅偑 n2/2 - 2 屄丆扨埵惓曽宍偑 1 屄丆1亊3 偺挿曽宍偑 1 屄偩偐傜丆嶍彍偟偨曈悢偼
| ( | n2 2 | - 2) + 1 + 2 = | n2 2 |
+ 1 杮 |
偲側偭偰偄傞丅偙傟偑嵟彫杮悢偱偁傞丅
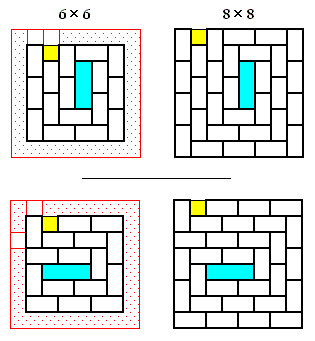
n亊n 偺応崌丆偙偺恾偵宖偘偨 2 偮偺僞僀僾偺偡傋偰偺夝偼丆揔摉偵夞揮傗棤曉偟傪峴偆偙偲偵傛傝丆奜廃偵愙偡傞扨埵惓曽宍乮墿乯傪 (1, 2) 偵抲偔偙偲偑偱偒傞 (忋偐傜 i 斣栚丆嵍偐傜 j 斣栚偺扨埵惓曽宍偺埵抲傪 (i, j) 偱昞偡偙偲偵偡傞)丅
偦偺偲偒丆1亊3 偺挿曽宍乮惵乯偺埵抲偼丆夝偺 2 庬椶偺僞僀僾偵墳偠偰
(n'-1, n'+1)乣(n'+1, n'+1) 傑偨偼 (n'+1, n'-1)乣(n'+1, n'+1) 偵側傞丅
偨偩偟丆n' = n/2 偲偍偄偨丅
n亞6 偺嬼悢偺応崌丆偙傟埲奜偺僞僀僾偺夝偑懚嵼偡傞偐偳偆偐偼妋偐傔偰偄側偄丅
側偍丆椉僞僀僾偺攝抲偼丆n亊n 偺攝抲偺奜廃乮6亊6偺恾偵偁傞愒榞晹乯偵偦傟偧傟婯懃揑側僷僞乕儞傪晅壛偟偰丆 偝傜偵婯懃揑側廋惓傪巤偡偙偲偵傛傝丆(n+2)亊(n+2) 偺攝抲偵奼挘偡傞偙偲偑偱偒傞丅
[2] n 偑婏悢偺応崌偼丆(n2 - 1)/2 杮偺扨埵曈傪嶍彍偡傞偙偲偵傛傝丆摨悢偺僪儈僲曅偲 1 屄偺扨埵惓曽宍偑偱偒傞丅
偙偺扨埵惓曽宍偑慡懱惓曽宍偺奜廃偵愙偡傞埵抲偵偁傝丆偦偺嫟桳曅傪 1 杮偩偗嶍彍偡傞偙偲偵傛傝戣堄傪枮偨偡偙偲偑
偱偒傟偽丆
(n2 - 1)/2 + 1 杮偺嶍彍偱幚尰偱偒傞偙偲偵側傞偑丆偦傟偼晄壜擻偱偁傞丅
側偤側傜丆壓恾偺傛偆偵扨埵惓曽宍 S (墿) 偺嵹傞曈忋偱丆S 偐傜墦偄曽偺捀揰偵僪儈僲曅傪抲偔偵偼嵍塃 2 捠傝偺 抲偒曽偑偁傝 (拲)丆偦偙偐傜恾偵帵偡傛偆側僪儈僲曅偺楢嵔偺攝抲偑偦傟偧傟昁慠揑偵寛傑傞偨傔丆塃壓偵 2亊2 偺惓曽宍偑偱偒傞偙偲偵側傞偑丆偙偺惓曽宍椞堟傪戣堄傪枮偨偟偰僪儈僲曅偱杽傔傞偙偲偼偱偒側偄偐傜偱偁傞丅
拲丗 n = 3 偺応崌丆S 偑曈偺拞墰偵偁傞応崌偼柧傜偐偵晄壜擻丆捀揰偵偁傞応崌偼嵍懁偺 1 捠傝偺傒丅
n = 5 偱 S 偑曈偺拞墰偵偁傞応崌偼嵍懁偺 1 捠傝偺傒偲側傞丅
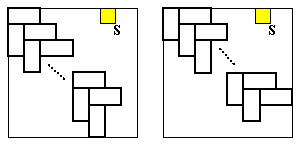
師偵丆(n2 - 1)/2 + 2 = (n2 + 3)/2 杮偺嶍彍偱嵪傓夝偲偟偰偼丆壓恾偺椺偵帵偡傛偆側塓姫偒宆偺攝抲傪尦偵偟偰丆 拞墰偺扨埵惓曽宍偺擟堄偺 1 曈傪嶍彍偟偰俴帤宆偺僺乕僗傪嶌傝丆偝傜偵奜廃偺擟堄偺扨埵曈傪嶍彍偟偰慡懱惓曽宍傪 徚偡偙偲偵傛傝摼傜傟傞傕偺偑偁傞丅
| 偙偺応崌偑 | n2+ 3 2 | 杮偱嵟彫杮悢偲側傞丅 |

| 埲忋 [1] 偲 [2] 傪傑偲傔偰丆嵟彫杮悢偼 [ | n2+ 3 2 | ] 杮偲側傞丅 |
亂姶憐亃
偙傟傑偱丆儅僢僠朹娭學偺僷僘儖偵恀柺栚偵庢傝慻傫偩偙偲偼側偐偭偨偺偱偡偑丆偙偺栤戣偼堦尒暯杴偵尒偊偰丆幚嵺偵夝偄偰傒傞偲堄奜偵墱怺偄偙偲偵嬃偒傑偟偨丅
寉偄婥帩偪偱庢傝偐偐偭偨偺偱偡偑丆擄廰偟偰偟傑偄傑偟偨丅
仧垽抦導丂Y.M.Ojisan 偝傫偐傜偺夝摎丅
亂栤戣侾亃 俁侽 屄
亂栤戣俀亃丂俋杮
庢傝曽偼壓恾愒攋慄
丂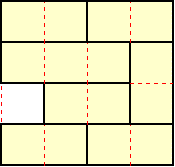 丂
丂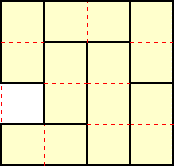
亂栤戣俁亅侾亃
墶曽岦偵丂俶杮偺儅僢僠偑俶亄侾抜偁傞丅廬偭偰
丂俀俶乮俶+侾乯杮
亂栤戣俁亅俀亃
侾亄俀俀亄俁俀亄丒丒丒丒亄N俀丂偱寁嶼偡傟偽傛偄丅
廬偭偰丄| 俶乮俶亄侾乯乮俀俶亄侾乯 俇 |
亂偍傑偗侾亃丂
幚幙丂栤戣俀偺夝摎偵帵偡俀屄偱偁傞丅
係亊係偺惓曽宍傪徚嫀偡傞偨傔偵丄彮側偔偲傕侾杮奜廃偺儅僢僠傪嵦傜側偗傟偽側傜側偄偑丄懳徧惈傪峫偊傞偲捀揰椬乮宯楍侾乯偲曈拞墰婑傝乮宯楍俀乯偺俀庬偺傒峫偊傟偽傛偄丅
偙偺堦杮偵傛傝侾亊侾偺惓曽宍侾屄偑嶍彍偝傟丄侾俆屄偑巆傞丅侾杮偺儅僢僠偱偼丄嵟戝俀屄偺侾亊侾偺惓曽宍偑徚嫀壜擻偱偁傞偐傜丄嵟掅偁偲俉杮昁梫偱偁傝丄崌寁俋杮偑嵟彫偱偁傞丅偙偺応崌丄儅僢僠傪庢傝嫀偭偨偁偲偵巆傞僞僀儖恾宍偼丄乮侾乯俇屄偺僪儈僲偲侾屄偺僩儕儈僲偐乮俀乯俈屄偺僪儈僲偲侾屄偺奜廃偺儌僲儈僲偱峔惉偝傟偰偄傞丅
偝傜偵丄俀亊俀偺惓曽宍偑徚嫀偝傟偰偄傞偨傔偵偼丄俀屄偺僪儈僲偑暯峴偵暲傫偱偄偰偼偄偗側偄丅
埲忋偺忦審傪枮懌偡傞僞僀儖偺暲傋曽傪俹俠偱扵嶕偡傞偲丄壓恾偵帵偡傕偺偩偗偱偁偭偨丅
側偍丄宯楍侾偺乮俀乯偼柍偐偭偨丅宯楍俀偺乮俀乯傕杮摉偼柍偐偭偨偺偱偁傞偑丄壓恾偵偼儌僲儈僲偑奜廃忋偺忦審傪偼偢偟偨傕偺傪帵偟偨丅
偝傜偵俁亊俁偺惓曽宍偑側偄傕偺傪扵偡偲丄宯楍俀偺乮侾乯僞僀僾偺俀屄偺傒偱偁偭偨丅
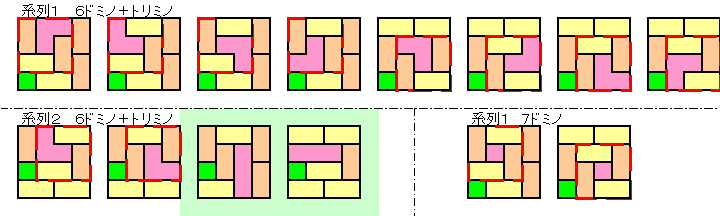
亂偍傑偗俀亃丂僈僂僗婰崋丂乵丂乶傪梡偄偰壓婰偱偁傞丅
偨偩偟丂俶亜侾
| [ | 俶俀亄俁 俀 |
] |
亂昁梫忦審亃
丂俶偑嬼悢偱偁傞応崌丄俶亊俶偺惓曽宍傪徚嫀偡傞偨傔偵奜廃偺侾杮傪庢傞偲丄侾亊侾偺惓曽宍偼侾屄徚嫀偝傟傞偩偗偱偁傝丄巆傝乮俶俀亅侾乯屄傪徚嫀偡傞偵偼丄乮俶俀亅侾乯偑婏悢偱偁傞偺偱丄俶俀偺敿暘偺儅僢僠傪庢傝彍偐側偗傟偽側傜側偄丅
傛偭偰丄嵟弶偺奜廃偺侾杮傪壛偊寁嶼偡傞偲丂摎偊偲摍壙偱偁傞丅
丂俶偑婏悢偱偁傞応崌丄嬼悢偺応崌偲摨偠峫偊曽傪揔梡偡傞偲丄乮俶俀亅侾乯偑嬼悢偱偁傞偺偱丄摎偊傛傝侾彮側偄昁梫忦審偲偟偰偺抣偑摼傜傟傞丅
偟偐偟幚嵺偼壓恾偵帵偡傛偆偵丄巆偝傟偨乮俶俀亅侾乯屄偺僙儖傪偦偺敿暘屄偺僪儈僲偱俀亊俀偺惓曽宍偑偱偒側偄傛偆偵杽傔傞偙偲偼晄壜擻偱偁傝丄摎偊偲摍壙偲側傞丅
亙壓恾夝愢亜
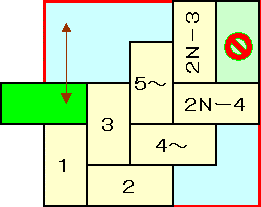
俶亞俆偺応崌丄奜廃偐傜庢偭偨侾杮偵傛傝徚嫀偝傟傞侾亊侾偺惓曽宍丗俧偲姳徛偟側偄懳妏慄偍傛傃偦偺椉懁傪尒偮偗傞偙偲偑偱偒傞丅
妏偵僪儈僲傪偍偄偰埲崀俀亊俀偺惓曽宍偑偱偒側偄傛偆偵懳妏慄忋偵僪儈僲傪抲偄偰峴偔偲乽岄偺巐挌乿偺傛偆偵嵟廔揑偵俀亊俀偺惓曽宍傪夞旔偱偒側偔側傞丅
廬偭偰丄彮側偔偲傕傕偆堦偮梋暘偵儅僢僠偺彍嫀偑昁梫偱偁傞丅
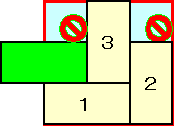
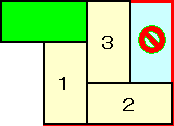
俶亖俁偺応崌傕壓恾偵帵偡傛偆偵係屄偺僪儈僲偱杽傔恠偔偡偙偲偑偱偒側偄丅
| 俶亞俆 | 俶亖俁丂宯楍俀 | 俶亖俁丂宯楍侾 |
 |
 |
 |
亂廫暘忦審亃
俶偑嬼悢偐婏悢偐偵傛傝丄壓恾偺傛偆偵丂朹忬僩儕儈僲側偄偟撌忬僥僩儘儈僲傪拞怱偵僪儈僲偑俀廳塓姫偒慄傪昤偔傛偆偵偐偮儗儞僈愊傒偺偺偆偵屳偄堘偄偵側傞傛偆偵攝抲偟丄俶亊俶偺斦柺乮揰慄乯傪峫偊傟偽丄廫暘忦審偲側偭偰偄傞帠偑傢偐傞丅
| 婏悢偺応崌 | 嬼悢偺応崌 |
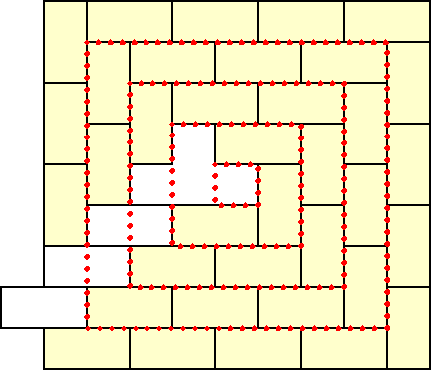 |
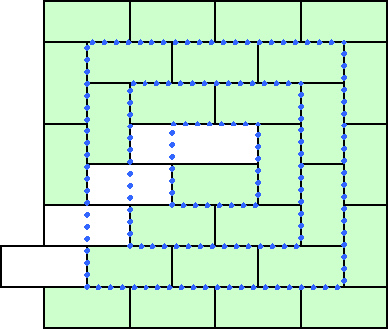 |
佹丂慡懱偑僪儈僲偐傜僥僩儘儈僲偱杽傔傜傟偰偄傞偺偱彮側偔偲傕侾亊侾偺惓曽宍偼徚嫀偝傟偰偄傞丅
俀亊俀埲忋偺惓曽宍偱徚嫀偝傟偰偄側偄傕偺偑偁傞偲偡傞偲丄挿偝俀埲忋偺捈慄偱峔惉偝傟偨俉埲忋偺挿偝偺暵偠偨愜傟慄偑昁梫偱偁傞丅
丂塓姫偒慄偵増偆曽岦偵偼丄挿偄楢懕愜傟慄偑懚嵼偟偰偄傞丅
偟偐偟巒揰偵栠傞偵偼丄俀埲忋偺挿偝偵搉偭偰墶抐偟側偗傟偽側傜側偄偑丄墶抐曽岦偵俀埲忋偺捈慄偼懚嵼偟側偄丅
傛偭偰丄俀亊俀埲忋偺惓曽宍傕徚嫀偝傟偰偄傞丅
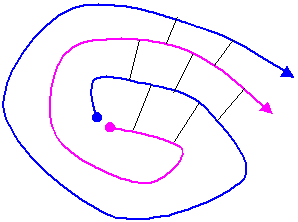
亂俹俽亃
偍傑偗侾偺扵嶕傪俹俠偱峴偄傑偟倲偑丄忦審偑尩偟偄偺偱扵嶕悢偼彮側偔丄幚偼恖娫媄偱傕廫暘壜擻偱偟偨丅
丂仧 栤戣傊傕偳傞
丂仧 崱廡偺栤戣傊