いろいろな解答がきたので、なかにはよくわからないものもあるのですが、とりあえず掲載します。
◆広島県 清川 育男 さんからの解答
【問題1】○○○○×○
○×○○○○
○○○×○○
×○○○○×
○○×○○○
○○○○×○
7個
【問題2】○○○○×○○
○○×○○○○
×○○○○×○
○○○×○○○
○×○○○○×
○○○○×○○
○○×○○○○
9個
【問題3】
48通り。(盤を固定して)
◆千葉県 菜花子 さんからの解答
【問題1】
7個の○を置き換えれば、条件を満たすことができる。

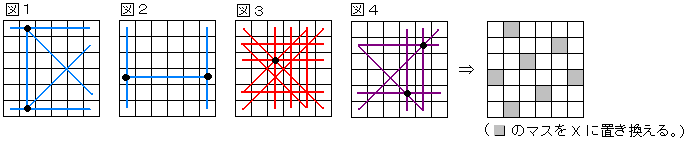
(1,2)と(6,2)を×に置き換える。
すると、図1の青の線のところが条件を満たす。
次に(4,1)と(4,6)を×に置き換える。
すると、さらに図2の青の線のところが条件を満たす。
青の線を引いていないところに、図3のように赤の線を引く。
一番多くの線(4本)が交わるマス(3,3)を×に置き換える。
まだ条件を満たしていないところに、図4のように紫の線を引く。
一番多くの線(3本)が交わるマス(2,5)(5,4)を×に置き換える。
【問題2】
9個の○を置き換えれば、条件を満たすことができる。
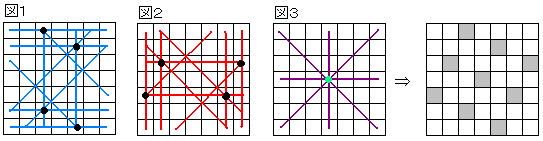
(1,3)(6,3)、(2,5)(7,5)を×に置き換える。
すると、図1の線のところが条件を満たす。
同様に(3,2)(3,7)、(5,1)(5,6)を×に置き換える。
すると、図2の線のところが条件を満たす。
まだ条件を満たしていないところに、図3のように線を引く。
全ての線が交わるマスを×に置き換える。
【問題3】
48通り
◆静岡県 medaka さんからの解答
【問題1】
7個○×○○○○
○○○○×○
○○×○○○
×○○○○×
○○○×○○
○×○○○○
【問題2】
9個○○○○×○○
○○×○○○○
×○○○○×○
○○○×○○○
○×○○○○×
○○○○×○○
○○×○○○○
【問題3】
プログラム(最後に添付)による探索の結果、反転対称解(鏡像解)を同一として数えた場合は、以下の11個。
別物とした場合は、48個
1 : ( 0, 0 ) ( 1, 1 ) ( 2, 2 ) ( 3, 3 ) ( 4, 4 )
2 : ( 0, 0 ) ( 1, 1 ) ( 2, 2 ) ( 3, 4 ) ( 4, 3 )
3 : ( 0, 0 ) ( 1, 2 ) ( 2, 3 ) ( 3, 1 ) ( 4, 4 )
4 : ( 0, 0 ) ( 1, 2 ) ( 2, 4 ) ( 3, 1 ) ( 4, 3 )
5 : ( 0, 0 ) ( 1, 3 ) ( 2, 2 ) ( 3, 1 ) ( 4, 4 )
6 : ( 0, 0 ) ( 1, 3 ) ( 2, 2 ) ( 3, 4 ) ( 4, 1 )
7 : ( 0, 0 ) ( 1, 3 ) ( 2, 4 ) ( 3, 1 ) ( 4, 2 )
8 : ( 0, 0 ) ( 1, 3 ) ( 2, 4 ) ( 3, 2 ) ( 4, 1 )
9 : ( 0, 0 ) ( 1, 4 ) ( 2, 2 ) ( 3, 3 ) ( 4, 1 )
10 : ( 0, 1 ) ( 1, 0 ) ( 2, 2 ) ( 3, 4 ) ( 4, 3 )
11 : ( 0, 1 ) ( 1, 4 ) ( 2, 2 ) ( 3, 0 ) ( 4, 3 )
【おまけ】最小の×の数をR(n)、n=5*k+m(kは自然数、mは0〜4の整数)とすると、
R(n)=5*k2 + 2*k*m + δ(m)
ただし、
δ(M)= 0 m=0,1,2の場合
δ(M)= 1 m=3の場合
δ(M)= 3 m=4の場合
(説明)
境界を意識しないで済むような大きなパネル上に○が敷き詰められているものとする。
このパネル上に×のマークを桂馬跳びの要領で以下の図のようにつけていく。
注:見易さために、×の代りに●で表示
5個毎に仕切り(−,|)を入れてあるが、この仕切りは無視してよい
(斜めの関係を見るときはない方がよい)
●○○○○|●○○○○|●○○○○ ○○○●○|○○○●○|○○○●○ ○●○○○|○●○○○|○●○○○ ○○○○●|○○○○●|○○○○● ○○●○○|○○●○○|○○●○○ ------------------------------ ●○○○○|●○○○○|●○○○○ ○○○●○|○○○●○|○○○●○ ○●○○○|○●○○○|○●○○○ ○○○○●|○○○○●|○○○○● ○○●○○|○○●○○|○○●○○ ------------------------------ ●○○○○|●○○○○|●○○○○ ○○○●○|○○○●○|○○○●○ ○●○○○|○●○○○|○●○○○ ○○○○●|○○○○●|○○○○● ○○●○○|○○●○○|○○●○○この配置には以下のような特徴がある。
(1)任意の×とその隣の×との距離は、縦・横・斜めの全てが丁度4つの○を間に置いている
(2)任意の位置から5x5のパネルを切り出すと、丁度5個の×が含まれる
(3)任意の位置から5xm又はmx5のパネルを切り出すと、丁度m個の×が含まれる
(1)から、×の配置の仕方として全く無駄のないものとなっている。
従って、このパネルからnxnの小パネルを切り出す場合に、×の数が最小となるような位置を選定すれば、nxnの求める答えの1つとなる。
具体的な×の数を求めるため、
n=5*K+m (m=0〜4)として、nxnのパネルを以下の小パネルに分解して考える。
a)5kx5kのパネル
b)5kxmのパネル
c)mx5kのパネル
d)mxmのパネル
a)は、5x5のパネルがk2個と考えることができるので、
上記の(2)により×の数は、その位置によらず、5*k2個となる。
また、b),c)も5xm、mx5のパネルがk個と考えられるので、上記の(3),(4)により
×の数は、その位置によらず、それぞれがk*m個となる。
d)のmxmのパネルの場合は、どの位置に配置するかに依存して×の数が変わる。
×の最小となる数をδ(m)とすると、以下のようになる。
(最初の図を良く見るとわかる)
δ(m)=0 m=0,1,2の場合
δ(m)=1 m=3の場合
δ(m)=3 m=4の場合
以上をまとめると、以下の式となる。
R(n)=5*k2 + 2*k*m + δ(m)
なお、問題1,2の場合は、それぞれR(6)=7,R(7)=9となる。
----------- 問題3の探索プログラム -----------
def exe() :
out = open("log.txt","w")
M = 5
C = 0
D = 0
for hash in range(0,120) :
Pos = toPos(hash,M)
if Check(Pos) == 0 : continue
D += 1
if DupCheck(Pos,out) == 0 : continue
C += 1
Line = " %3d : " % (C)
for k in range(0,5) : Line += " ( %d, %d )" % (k,Pos[k])
WriteLog(out,Line)
Check(Pos)
WriteLog(out," Dup %d " % (D))
out.close()
###
def Check(Pos) :
U = 0
V = 0
for i in range(0,len(Pos)) :
j = Pos[i]
if (i == j) : U = 1
if (i+j == 4) : V = 1
if (U == 0) | (V == 0) : return 0
return 1
##
def toPos(Hash,M) :
h = Hash
Pos = []
for k in range(0,M) : Pos += [0]
for k in range(0,M) :
n = 6 - M + k
p = h % n
h = h / n
Pos[M-k-1] = p
for i in range(M-2,-1,-1) :
for j in range(i+1,M) :
if Pos[i] <= Pos[j] : Pos[j] += 1
return Pos
##
def DupCheck(Pos,out) :
for t in range(0,8) :
w = Pos
if (t & 0x01) != 0 :
u = [[],[],[],[],[]]
for k in range(0,len(Pos)) : u[k] = 4 - w[k]
w = u
if (t & 0x02) != 0 :
u = [[],[],[],[],[]]
for k in range(0,len(Pos)) : u[k] = w[4-k]
w = u
if (t & 0x04) != 0 :
u = [[],[],[],[],[]]
for k in range(0,len(Pos)) : u[w[k]] = k
w = u
if Pos > w : return 0
return 1
###
def WriteLog(out,Line) :
print Line
out.write(Line+"\n")
out.flush() ◆東京都 ぽこぺん さんからの解答
【問題1】
※この解答では見やすさのために×の代わりに●で表します。
最初に,一般の配置に対する十分条件を与える。
平面上の格子点に
{ (5k+m, 5l+2m) | k, l, m∈Z } (1)
で表される点●を配置すると (下図),縦,横,斜めのいずれの方向にも5個連続して○が並ぶことはない。
また,
{ (5k+2m, 5l+m) | k, l, m∈Z } (2)
で表される点を配置しても同じ条件を満たす。
○○●○○○○●○○○○●○○○○●○○ ○○○○●○○○○●○○○○●○○○○● ○●○○○○●○○○○●○○○○●○○○ ○○○●○○○○●○○○○●○○○○●○ ●○○○○●○○○○●○○○○●○○○○ ○○●○○○○●○○○○●○○○○●○○ ○○○○●○○○○●○○○○●○○○○● ○●○○○○●○○○○●○○○○●○○○ ○○○●○○○○●○○○○●○○○○●○ ●○○○○●○○○○●○○○○●○○○○ ○○●○○○○●○○○○●○○○○●○○ ○○○○●○○○○●○○○○●○○○○● ○●○○○○●○○○○●○○○○●○○○ ○○○●○○○○●○○○○●○○○○●○ ●○○○○●○○○○●○○○○●○○○○ ○○●○○○○●○○○○●○○○○●○○ ○○○○●○○○○●○○○○●○○○○● ○●○○○○●○○○○●○○○○●○○○ ○○○●○○○○●○○○○●○○○○●○ ●○○○○●○○○○●○○○○●○○○○【問題1】
最少7個で,配置はたとえば:○○○○●○
○●○○○○
○○○●○○
●○○○○●
○○●○○○
○○○○●○
【問題2】
最少9個で,配置はたとえば:
○○●○○○○
○○○○●○○
○●○○○○●
○○○●○○○
●○○○○●○
○○●○○○○
○○○○●○○
【おまけ】
n×n に並ぶ n2 個の格子点において,
連続して並ぶ 5 個のうちの少なくとも 1 個が●になるには,
| 全体で少なくとも[ | n2 5 | ] 個の●が必要である。 |
逆に(1)または(2)の配置において,n×n の部分配置をうまく選べば,
| ●の個数をちょうど[ | n2 5 | ] 個とすることができるので, |
【その証明】
n≧0 の各整数 n に対して,n×n の正方形領域の内部に含まれる●の個数の最小値を f(n) とする。
(1)の配置において,n×n の正方形領域で,左下隅が原点に当たるものを考えると,その中の縦の各列に含まれる●の個数は:
| x=0 のとき 0≦y≦(n-1) の範囲に[ | n+4 5 | ] 個 |
| x=1 のとき 0≦y≦(n-1) の範囲に[ | n+2 5 | ] 個 |
| x=2 のとき 0≦y≦(n-1) の範囲に[ | n 5 | ] 個 |
| x=3 のとき 0≦y≦(n-1) の範囲に[ | n+3 5 | ] 個 |
| x=4 のとき 0≦y≦(n-1) の範囲に[ | n+1 5 | ] 個 |
以下,これの繰り返しとなる。
f(n) を求めるには,必要があればこの正方形領域を右に平行移動して,●の個数を数える。
0≦n<5 に対しては次のようになる:
f(0) = 0 (平行移動しない)
f(1) = 0 (右に 1 平行移動する)
f(2) = 0+0 = 0 (右に 1 平行移動する)
f(3) = 0+1+0 = 1 (右に 2 平行移動する)
f(4) = 0+1+1+1 = 3 (右に 2 平行移動する)
n≧5 に対しては,平行移動量を同じとして
f(n+5) = f(n) + 2n + 5となる。
(∵下図でAの領域が f(n),BとCが n,Dが 5)
| この漸化式を解くとf(n) = | n2−a 5 |
| f(n) =[ | n2 5 | ] と書ける。 |
□□□■■■■■ □□□■■■■■ □B□■■D■■ □□□■■■■■ □□□■■■■■ ■■■□□□□□ ■A■□□C□□ ■■■□□□□□【感想】
最後の証明は,もっとスマートに行う方法があるかと思うのですが,場合分けを使って力づくでやってしまいました。
◆東京都 綾 さんからの解答
【問題1】
桂馬飛びで7つ○×○○○○
○○○×○○
×○○○○×
○○×○○○
○○○○×○
○×○○○○
【問題2】
桂馬飛びで9つ○○×○○○○
○○○○×○○
○×○○○○×
○○○×○○○
×○○○○×○
○○×○○○○
○○○○×○○
【問題3】
まず、5×5の中心に×を置かない場合、第3行目に置ける位置は4つあります。
対角線上に×印がある条件に注意すると、それぞれの位置について、可能な配置は次の例に示すように6通りあります。
×○○○○ ×○○○○ ○○×○○ ○○×○○ ○○○○× ○○○○× ○○○×○ ○○○×○ ○○○×○ ○○○○× ○○×○○ ×○○○○ ○×●○○ ○×●○○ ○×●○○ ○×●○○ ○×●○○ ○×●○○ ○○○○× ○○×○○ ×○○○○ ○○○×○ ○○○×○ ○○○×○ ○○×○○ ○○○○× ○○○○× ×○○○○ ×○○○○ ○○×○○よって、5×5の中心に×を置かない配置は全部で4×6通り
次に、5×5の中心に×を置く場合を考えます。
対角線上にある条件は満たされています。
したがって、これは4!通り。
以上から、4!+4×6=48通り。
対称なものを排除するとさらに減ります。
【おまけ】
一階差分数列 元の数列 番号No [(No+2)/5]n 0,0,2,1,2,2,2, 0, 0, 5, 7, 9 3, 4, 5, 6, 7, 1 4,3,4,4,4, 13,16,20,24,28, 8, 9,10,11,12, 2 6,5,6,6,6, 34,39,45,51,57, 13,14,15,16,17, 3 8,7,8,8,8 65,72,80,88,96, 18,19,20,21,22, 4これから、A(k)をk×kのときの最小数とすると、n≧2のとき、
A(5n-2)=5n2-4n+1
A(5n-1)=5n2-4n+1+2n-1=5n2-2n
A(5n)=5n2-2n+2n=5n2:n≧1
A(5n+1)=5n2+2n:n≧1
A(5n+2)=5n2+4n:n≧1
面白かったです。桂馬飛びはなかなか気が付きませんでした。
◆東京都 JAVAKnight さんからの解答×○○○○
○○○×○
○×○○○
○○○○×
○○×○○
nが5以上のとき、縦n横nの升目に上記パターンを繰り返しはりつけることを考える。
これによって、縦横斜めどの方向にも4個以下しか○が連続で並ばない。
n=6の場合は、7個の×が必要である。
なぜなら6個のみでは、縦5つ並んではいけないという条件から、各列に1個の×が必要で、横5つ並んではいけないという条件からすべての行に×が現れる必要があり、そうするとどこかの列で端のみに×が現れるということになるからだ。
7個の場合は容易に例を構成できる。
n=7の場合、9個の×では容易に例を構成できる。
一方、n=6のとき×が7個必要だったから、縦横1行ずつ増えた場合は×が9個必要であることがわかる。
この考察により、nを5で割った余りが0,1,2のときの×の最小個数は容易に分かる。
kが1以上の整数のとき、
n=5kなら、×は5k2個であり、
n=5k+1なら×は5k2+2k個であり、
n=5k+2なら×は5k2+4k個である。
n=5のとき、縦横に○が5個以上並ばない×の置き方は120通りある。
全ての場合を調べると、斜めにも○が5個以上並ばない×の置き方は48通りあることがわかる。
◆愛知県 迷子の雄猫 さんからの解答
【問題3】
5個の配置は5*4*3*2*1=120通り
うち、72通りは対角線上にX印が無いから、
xが5個ならんでいないのは48通り
(鏡像、回転を考えると実質6通り、でしょうか。)
【問題4】
とある一列を考えると、最小個数にするためにはxとxの間にOが4個並んでいる必要がある。
左端から数えて、Oがa個並んでいる列を「a」であらわす。
「3」「1」「4」「2」「0」の順で繰り返し並べると、縦横斜めとも、xとxの間にOが4個並ぶ。
さて、それぞれの列にはxが何個有るだろうか?
「3」の場合、列の左端から3個のOを切り取ると、
XOOOOの繰り返しになるから、xの個数は
| n−3 5 | 個(端数切り上げ)= | n−3+4 5 | 個(端数切り捨て) |
| つまり | n+1 5 | 個(端数切り捨て)である。 |
同様に
| 「4」の場合 | n+0 5 | 個(端数切り捨て) |
| 「3」の場合 | n+1 5 | 個(端数切り捨て) |
| 「2」の場合 | n+2 5 | 個(端数切り捨て) |
| 「1」の場合 | n+3 5 | 個(端数切り捨て) |
| 「0」の場合 | n+4 5 | 個(端数切り捨て) |
nを5で割った商をr、余りをmとする。
nが5で割り切れないとき、5で割り切れない部分には、
「3」「1」「4」「2」「0」の順であれば任意の列を並べることが出来る。
もちろん、k4≦k3≦k2≦k1≦k0であるから、
m=0の場合、
(k3+k1+k4+k2+k0)*r
m=1の場合、
(k3+k1+k4+k2+k0)*r+k4
m=2の場合、
(k3+k1+k4+k2+k0)*r+k4+k2
m=3の場合、
(k3+k1+k4+k2+k0)*r+k3+k1+k4
m=4の場合、
(k3+k1+k4+k2+k0)*r+k3+k1+k4+k2
◆東京都 明 さんからの解答
【問題1】
盤面の縦または横に連続して並んだ5目の列(以後簡単のため単に「セル」と呼びます)には少なくとも1つの×がなくてはなりません。
6×6の盤面では、明らかに、重ならない7個のセルを選択することができます。
従って、条件を満たす×の最小値M≧7
実際、以下の配置は×が7個で条件を満たしています。
よって、最小値M=7○×○○○○
○○○×○○
×○○○○×
○○×○○○
○○○○×○
○×○○○○
【問題2】
【問題1】と同様に7×7の盤面では9個の重ならないセルを選択することができます。
従って、M≧9
実際、以下の配置は×が9個で条件を満たしています。
よって、最小値M=9○○×○○○○
○○○○×○○
○×○○○○×
○○○×○○○
×○○○○×○
○○×○○○○
○○○○×○○
【問題3】
×が止める行と列が全て異なるような配置で、下図のa〜dおよびe〜hの斜めの2列に×が少なくとも1つ含まれる配置の数を求めることになります。a○○○e
○b○f○
○○o○○
○g○c○
h○○○d
oが×のときは、斜め2列に×が1つ含まれます。
この時、×が止める行と列が全て異なるような配置の数は
4!=24
次にoが○の時、条件を満たす数を求めます。
×が止める行と列が全て異なるような配置の条件下で、
N(x∪y)を、e〜hのいずれかが×(oは除く)でxまたはy
(x、yはa〜dのいずれか)のいずれかが×である場合の数、
N(x∩y)を、e〜hのいずれかが×(oは除く)でx,y共に×である場合の数と定義します。
求める数はN(a∪b∪c∪d)となります。
N(a∪b∪c∪d)
=N(a)+N(b)+N(c)+N(d)
−N(a∩b)・・・−N(c∩d)
(a〜dからの2つの組み合わせすべて)
+N(a∩b∩c)・・・+N(b∩c∩d)
(a〜dからの3つの組み合わせすべて)
−N(a∩b∩c∩d)
N(a)=N(d)=2×2×2−1
N(b)=N(c)=2×2×2−1
N(a∩d)=N(b∩c)=2
N(他の組み合わせ)=0
よって
N(a∪b∪c∪d)=4×(2×2×2−1)−2×2=24
以上より条件を満たす配置の数は48となります。
【おまけ】
n×nでの最小値Mを求めるために、まず5×5の4つをつなげて10×10の盤面を考えます。
1つの5×5の盤面で、×が止める行と列が全て異なるような配置とした場合、○の5連ができないように10×10の盤面を配置すると、4つの5×5の盤面の配列がすべて同一になります。
この条件で、斜めに5連ができないような配置を考えると、斜めの連続した5目からなる列も、×は唯1つである必要があります。
(さもないと×の数が斜めでカウントしたとき、増えてしまいます。)
この状況では、盤面の配置は、1箇所の×を決めると自動的に2つの形が求まります。
左上隅を×とした場合は以下のとおり。×○○○○
○○×○○
○○○○×
○×○○○
○○○×○
×○○○○
○○○×○
○×○○○
○○○○×
○○×○○
この配置に、上下または左右にセルを追加したとき、○の5連ができないようにし、かつ×の数を最小化しようとすると、追加したセルの×の位置は決定され、×の数は追加したセルの数に一致します。
次に8×8と9×9の盤面の最小値Mを求めます。
8×8のとき、下記のように重ならないセルは12あります。aaaaadef
bbbbbdef
cccccdef
hijxxdef
hijxxdef
hijkkkkk
hijlllll
hijmmmmm
よって、M≧12
実際下記配置が条件を満たし、よってM=12○○○×○○○○
○×○○○○×○
○○○○×○○○
○○×○○○○×
×○○○○×○○
○○○×○○○○
○×○○○○×○
○○○○×○○○
9×9のとき、
同様にして重ならないセルは16あることがわかります。
下記配置が条件を満たし、よってM=16○○○○×○○○○
○○×○○○○×○
×○○○○×○○○
○○○×○○○○×
○×○○○○×○○
○○○○×○○○○
○○×○○○○×○
×○○○○×○○○
○○○×○○○○×
以上からn×nの最小値Mは
n=5k+j (j=0〜4)として
M=5k2+2kj+R(j)
ただし
R(j)=0 j=0,1,2
R(j)=1 j=3
R(j)=3 j=4
◆愛知県 Y.M.Ojisan さんからの解答
【問題1】 7個
| ○×○○○○ ○○○○×○ ○○×○○○ ×○○○○× ○○○×○○ ○×○○○○ |
【問題2】 9個
| ○○○○×○○ ○○×○○○○ ×○○○○×○ ○○○×○○○ ○×○○○○× ○○○○×○○ ○○×○○○○ |
【問題3】 48通り
(1)下左図のように中央を×にした場合、斜めの防手は済みなので残り4!=24とおり可能である。
(2)中央を〇とした場合、中央ライン上は左右、上下、内外行列入れ替えの8対称を考慮すると下右図のように上辺中央に限ってよい。すると5個で斜めを防ぐには左下隅(右下隅は対称で考慮)が必須である。
残り3×3〇を用いて完全に防手とできるのは、可能性のある3!通りを調べると、その内3通りである。よって、3×8=24通りである。
(3)即ち 合計48とおり。
|
○○●○○ ○○●○○ ●●×●● ○○●○○ ○○●○○ |
●●×●● ●○●○○ ●○◎○○ ●○●○○ ×●●●● |
G=[N/5] F=N mod 5 とするとき
G*(N+F)+max( 0 , 2*F-5)
計算すると下記である。
実際の並べ方は問題2、3に示した規則的な並べ方(♯配置とよぶ)である。
| N | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| × | 5 | 7 | 9 | 12 | 16 | 20 | 24 | 28 | 33 | 39 | 45 | 51 | 57 | 64 | 72 | 80 |
【理由】
ある一列(行)を防ぐのに G=[N/5]個は最低必要である。
従って、Nが5の倍数のときは最低N2/5=GN 個必要である。
これは、#配置で実現可能である。
F=1の場合、少なくとも両端の各列にG個ずつ防手を配置する必要があるので、この場合配置された行は×G個では防ぎ切れない。
よって余分に少なくともG個必要である。
即ち、GN+G個必要である。
これも#配置で実現可能。
F=2の場合、少なくとも両端の各2列にG個ずつ防手を配置する必要があるので、この場合配置された行は×G個では防ぎ切れない。
左2列の×を同じ行に配置しても防手効果は改善しないので、少なくとも余分に2G個必要である。
即ち、GN+2G個必要である。
これも#配置で実現可能。
F=3の場合、少なくとも両端の各3列にG個ずつ配置する必要があるので、この場合配置された行は×G個では防ぎ切れない。
左3列の×を同じ行に配置しても防手の効果は改善しないので、少なくとも余分に3G個必要である。
さらにこの関係は上下方向にも考えなければならず、F=3になると両端の各3列のうち一列はG+1個の防手をしなければならない。
よって、GN+3G+1個必要である。
これも#配置で実現可能。
F=4の場合、少なくとも両端の各4列にG個ずつ配置する必要があるので、この場合配置された行は×G個では防ぎ切れない。
左4列の×を同じ行に配置して防手の効果は改善しないので、少なくとも余分に4G個必要である。
さらにこの関係は上下方向にも考えなければならず、F=4になると両端の各4列のうち3列はG+1個の防手をしなければならない。
よって、GN+4G+3個必要である。
これも#配置で実現可能。
以上まとめると
GN+FG+K(F)
K(F)=(0、0、0、1、3)=max(0,2F-5)である。
◆ 問題へもどる
◆ 今週の問題へ