◆広島県 清川 育男 さんからの解答
【問題1】 1 3
| |
9―2―4
| |
8 6
1=1,2=2,3=3,
4=2*2,
5=5,
6=2*3,
7=7,
8=2*2*2,
9=3*3
2の素因数は7個
3の素因数は4個
5の素因数は1個
7の素因数は1個
したがって、5、7は使えない。
また2は中央に入らなければならない。
3つの数の積の中に2の素因数は3個、3の素因数は2個。
したがって、3つ数の積は72。1 3
□ 2 □
□ □
-----------
1 3
9 2 4
8 6
上下、左右が交換可能であるから、8通り。
【おまけ1】
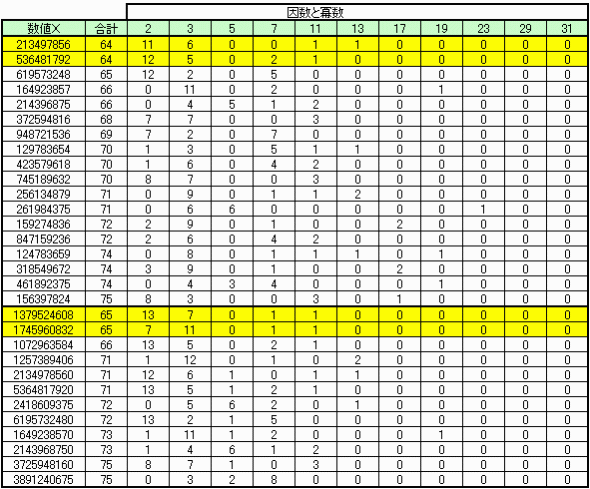
213497856=211*36*11*13 ,64
536481792=212*35*72*11 ,64
【おまけ2】
1379524608=213*37*7*11 ,65
1745960832=27*311*7*11 ,65
◆三重県 とくしん さんからの解答
【おまけ1・2】
9桁、10桁の場合において合計が70未満になるのはこれで全てです。0213497856:64,2*11,3*6 ,11*1,13*1
0536481792:64,2*12,3*5 ,7 *2,11*1
0619573248:65,2*12,3*2 ,7 *5
0164923857:66,3*11,7*2 ,19*1
0214396875:66,3*4 ,5*5 ,7 *1,11*2
0372594816:68,2*7 ,3*7 ,11*3
0948721536:69,2*7 ,3*2 ,7 *7
1379524608:65,2*13,3*7 ,7 *1,11*1
1745960832:65,2*7 ,3*11,7 *1,11*1
1072963584:66,2*13,3*5 ,7 *2,11*1
左からX、合計、因数の種類と数です。
0〜9の順列を作る部分が一番苦労しました(笑)
◆愛知県 Y.M.Ojisan さんからの解答
【問題1】
対称性を考慮すると1種のみ3 1
| |
4―2―9
| |
6 8
【導出法】A E
BDF
C G
としたとき
A*B2*C*D*E*F2*G=X3
でなければなりません。
(1)従ってX3の素因数冪数が2以上にならない5と7は使えません。
のこりは丁度7個です。
(2)素因数3を生むのは 3(1個)、6(1個)、9(2個)です。
従ってX3の3の冪数は4〜7個であり、3の倍数は6のみです。
冪数6になるには3か9はBかFにある必要があります。
(3)素因数2を生むのは 2(1個)、4(2個)、6(1個)、8(3個)です。
従ってX3の2の冪数は7〜12個であり、3の倍数は9か12です。
冪数12になるには、BとFは偶数でなければなりません。
しかし(2)によりそれは不可能です。
よって冪数は9です。
(4)以上からX=72です。
3個の積で72になるのは 1−8−9 2−4−9 3−4−6の3種のみです。
(5)よってB,Fに入るのは4と9です。
これよりD=2です。
【おまけ1解答】
X=213497856 合計=64 等 下表参照
【おまけ2解答】
X=1379524608 合計=65 等 下表参照
【おまけのPC探索方法】
合計75以下を目標としてPC探索した方法を示します。
X=2P23P35P5・・・として
合計 =2*P2+3*P2+5*P5・・・ ≦75
log(X) =log(2)*P2+log(3)*P2+log(5)*P5・・・ ≦log(9876543210) & ≧log(123456789)を満足する Piを定め、Xを計算してそれが 0〜9だけでできているかチェックします。
ある因数の冪数は残りを全部2の冪でまかなうとして最大値を切ることができ、31まで考えれば良いことが判ります。
さらにXは9の倍数ですから3の冪は2以上です。
細かいところでは、2と5の冪数が共に2以上だとXの下2桁が00になるので、これは除外できます。
得られた結果で最上位が「0」のものがおまけ1の解で、その他がおまけ2の解です。

◆東京都 明 さんからの解答
【問題1】
裏返し、回転を同一と見ると、下記2通りのみ。8 3
| |
9―2―4
| |
1 6
1 3
| |
9―2―4
| |
8 6
以下のように考えました。
3数の積の3系統すべてに共通な項は存在しない。
従って、素因数分解の一意性により、1〜9の中の数で、2つ以上
の数に共通する素数を持たない数(5と7)は候補から外れます。
他の数を素因数分解します。
1 = 1
2 = 2
3 = 3
4 = 2・2
6 = 2・3
8 = 2・2・2
9 = 3・3
3の素因数に着目して、3系統で、3の素因数を同数にする配置は裏返し、回転を同一と見ると、下記一通りのみ。□ 3
| |
9―□―□
| |
□ 6
次に2の素因数に着目して、下記の3系統で、2の素因数を同数に
する配置を考えればよい。□ X
| |
X―□―□
| |
□ 2
以上から前記解を求めることができます。
【おまけ1】
2以上の整数では、2数の積 ≧ 2数の和。
従って、因数の和を最小にするためには素因数分解をすることになります。
和が100以下のヒントがあるので、後はしらみつぶしで素因数が100以下で構成される数列を検索し、和が最小のものを求めました。
数列 : 213497856 素因数合計 : 64
素因数 : 211 × 36 × 111× 131
数列 : 536481792 素因数合計 : 64
素因数 : 212 × 35× 72× 111
【おまけ2】
【おまけ1】と同様に求めました。
数列 : 1379524608 素因数合計 : 65
素因数 : 213× 3 7 × 71× 111
数列 : 1745960832 素因数合計 : 65
素因数 : 27× 311× 71× 111
参考で【おまけ2】のプログラムを添付します。
(10進BASIC)
---------------------------------------
DECLARE EXTERNAL SUB zyun
REM 素数データ
DATA 2 , 3 , 5 , 7 , 11
DATA 13 , 17 , 19 , 23 , 29
DATA 31 , 37 , 41 , 43 , 47
DATA 53 , 59 , 61 , 67 , 71
DATA 73 , 79 , 83 , 89 , 97
REM 数値列データ
DATA 1,0,2,3,4,5,6,7,8,9
DIM PN(25)
DIM N(10)
DIM CN(25)
MAT READ PN
MAT READ N
SUB number
LET NB=0
FOR J=1 TO 10
LET NB=NB+N(J)*10^(10-J)
NEXT J
END SUB
LET MIN=100
DO
CALL number
MAT CN=ZER
LET NC=NB
LET ID=1
LET SUM=0
DO
IF NC=1 THEN EXIT DO
IF MOD(NC,PN(ID))=0 THEN
LET NC=NC/PN(ID)
LET SUM=SUM+PN(ID)
LET CN(ID)=CN(ID)+1
ELSE
LET ID=ID+1
END IF
IF ID>25 THEN
LET SUM=101
EXIT DO
END IF
LOOP
IF MIN>=SUM THEN
LET MIN=SUM
PRINT "数列 : ";NB;" 素因数合計 : ";SUM
PRINT "素因数 : ";
LET BG=1
FOR J=1 TO 25
IF CN(J)<>0 THEN
IF BG=0 THEN PRINT "×";
LET BG=0
PRINT PN(J);"^";CN(J);
END IF
NEXT J
PRINT
PRINT
END IF
CALL zyun(10,EX,N)
LOOP UNTIL EX=0
PRINT "END"
END
!順列の変更
EXTERNAL SUB zyun(K,EX,N())
DECLARE EXTERNAL SUB seiretu
LET EX=0
LET J=1
DO
IF J>=K THEN EXIT DO
IF N(K-J)<N(K-J+1) THEN
CALL seiretu(J,K,N)
LET L=1
DO
IF N(K-J)>=N(K-J+L) THEN
LET L=L+1
ELSE
LET B=N(K-J)
LET N(K-J)=N(K-J+L)
LET N(K-J+L)=B
LET EX=1
EXIT DO
END IF
LOOP
EXIT DO
ELSE
LET J=J+1
END IF
LOOP
END SUB
!配列の整列
EXTERNAL SUB seiretu(J,K,N())
LET D=K-J+1
LET E=K
DO WHILE D<E
LET B=N(D)
LET N(D)=N(E)
LET N(E)=B
LET D=D+1
LET E=E-1
LOOP
END SUB
--------------------------------------
◆ 問題へもどる
◆ 今週の問題へ