『今週の問題』第184回　解答

◆愛知県　迷子の雄猫 さんからの解答

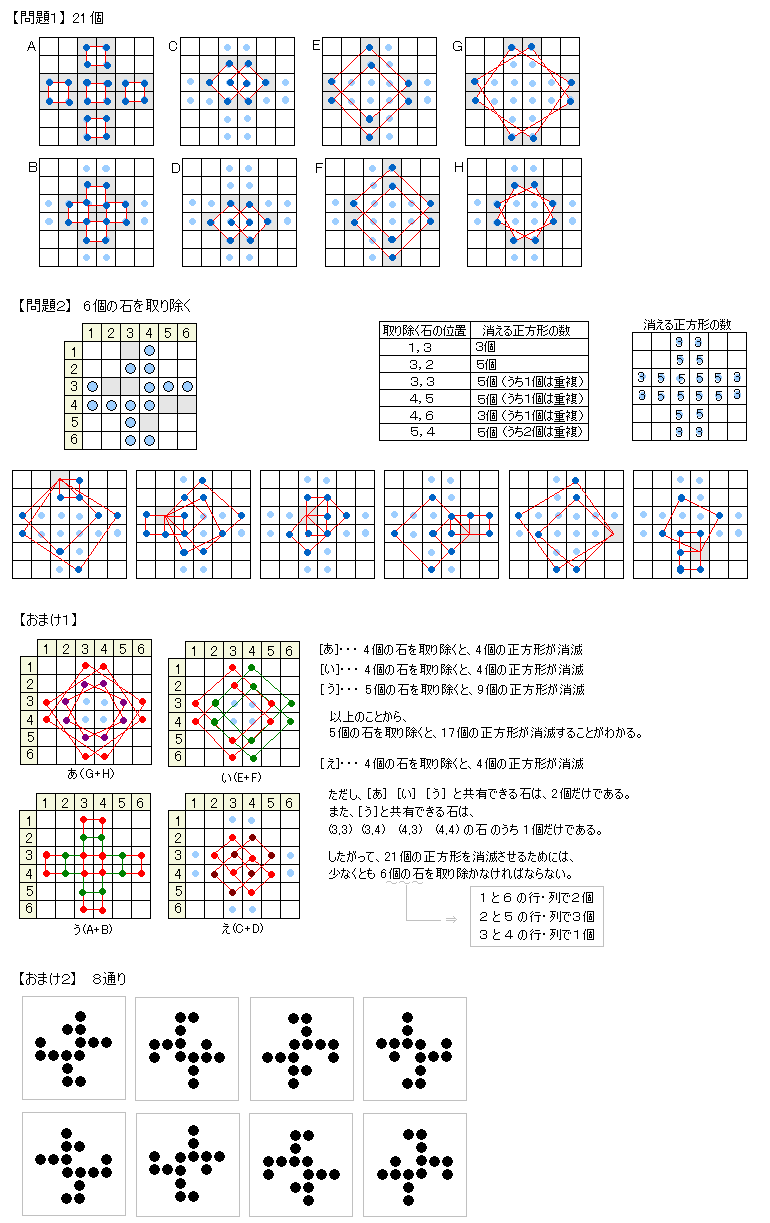
【問題１】

正方形２１個

【問題２】

石６個、

ＡＦＧＰＱＳ
　　　●　　
　　●●　　
●　　●●●
●●●●　　
　　●　　　
　　●●　　

上記の回転、鏡像の８通り

【おまけ１】

石に以下のとおり記号をつける。

−−ＡＢ−−
−−ＣＤ−−
ＥＦＧＨＩＪ
ＫＬＭＯＰＱ
−−ＲＳ−−
−−ＴＵ−−

ＡＫＵＪのなかからＡを選ぶと仮定しても一般性を失わない。

1. Ｂ，Ｔを選んだ場合：「ＣＤＧＨ」「ＭＯＲＳ」「ＥＦＫＬ」「ＩＪＰＱ」の４組から１つずつ石を選ぶ必要がある。
   よって最低６個の石を選ぶ必要がある。

2. Ｅを選んだ場合：まず「ＩＪＰＱ」「ＲＳＴＵ」の２組から１つずつ石を選ぶ必要がある。
   「ＣＤＧＨ」「ＦＧＬＭ」「ＧＨＭＯ」「ＣＦＭＨ」の全てに共通する石は無いから、あと２個、合計で最低６個の石を選ぶ必要がある。

3. Ｑを選んだ場合：まず「ＥＦＫＬ」「ＲＳＴＵ」の２組から１つずつ石を選ぶ必要がある。
   「ＣＤＧＨ」「ＨＩＯＰ」「ＧＨＭＯ」「ＤＧＯＩ」の全てに共通する石は無いから、あと２個、合計で最低６個の石を選ぶ必要がある。

◆愛知県　Y.M.Ojisan さんからの解答

【問題１】　２１個

【問題２】　６個

　　　●　　
　　●●　　
●　　●●●
●●●●　　
　　●　　　
　　●●　　

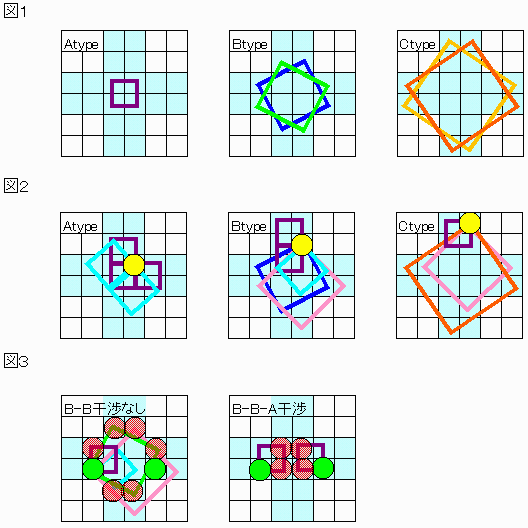
図１のように石を共有しない３タイプ（Ａ，Ｂ，Ｃ）５個の正方形がある。
従って、最低石を５個撤去する必要がある。
一方Ａの石は図２のように３個、Ｂは５個、Ｃは５個の正方形を消せる。
よって５個撤去の場合、最大5+2*5+2*3=21個の正方形を消去できる。
これはぎりぎりの数であり、無駄は許されない。
Ｂ−Ｂタイプ間で無駄のない撤去位置は図３のみであるが、これは必ずＡと干渉し無駄が発生する。
よって６個が最低である。

図１

【おまけ２】

１通り　（ＰＣ解です。）

対称性からＡTypeの撤去位置は左上に限定します。
すると、Ｂ、Ｃのケースを全て調べても４⁴＝２５６通りで、最終の必然手が有無を含め決まります。
２とおりの答えが出ましたが、それらは鏡像対称だったので実質１通りです。

◆東京都　明 さんからの解答

【問題１】

21個

【問題２】

取り除いた石の個数：6個
現在の形：

　　　●　　
　　　●　　
●　●●●●
●●●　●　
　　●　　　
　　●●

５個以下の個数を取り除くことでは不可能であることの説明

説明のために各石に以下のようにＡ〜Ｔの記号を付けます。

××ＡＢ××　
××ＣＤ××　　
ＭＮＱＲＥＦ
ＯＰＳＴＧＨ
××ＩＪ××　　
××ＫＬ××

Ａ〜Ｄ、Ｅ〜Ｈ、Ｉ〜Ｌ、Ｍ〜Ｐ、Ｑ〜Ｔで出来る５個の正方形は共通する石をもたないので、ｍ≧５であり、少なくとも 各正方形を構成する石から１個ずつを取り除く必要があります。

以下５個を除くことですべての正方形がをせるかを確認します。

ＡＦＬＯおよびＢＨＫＭは正方形であるので、少なくとも２個はそれぞれの正方形を構成する石から取り除かねばなりません。
対称性を考慮すると、この２個の石を取り除いたときに残る石は下記２つのパターン以上です。
ここでは、「以上」とは実際の形はパターンに幾つかの石が追加されたものであることを言います。
従って少なくともパターンに残された正方形は、残り３個を取り除くことで消されなければなりません。

（パターン１）

××××××　
××ＣＤ××　　
ＭＮＱＲＥＦ
ＯＰＳＴＧＨ
××ＩＪ××　　
××××××

××××××　
××ＣＤ××　　
ＭＮＱＲＥ×
ＯＰＳＴＧ×
××ＩＪ××　　
××ＫＬ××

２個の石を取り除いてＭ〜Ｐ、Ｅ〜Ｈの正方形を消すと、残った石は次のパターン以上です。

××××××　
××ＣＤ××　　
××ＱＲ××
××ＳＴ××
××ＩＪ××　　
××××××

パターン２の場合。

２個の石を取り除いてＭ〜Ｐ、Ｉ〜Ｌの正方形を消すと、残った石は次のパターン以上です。

××××××　
××ＣＤ××　　
××ＱＲＥ×
××ＳＴＧ×
××××××　　
××××××

以上の議論により、ｍ≧６であることが判ります。

【おまけ２】

第182回の『正方形の消滅』と同様のプログラムで８通りを確認しました。
従って、問題２の解が唯一の基本パターンで、この裏返し、回転の計８通りが解となります。

◆和歌山県　kasama さんからの解答

【問題１】

正方形の個数の個数は全部で21個あると思われます。
詳細は以下の通りです。
□印は正方形を構成する石の場所です。

(1)１辺の長さが1の正方形の個数・・・9個

　　□□　　
　　□□　　
●●●●●●
●●●●●●
　　●●　　
　　●●　　

　　●●　　
　　□□　　
●●□□●●
●●●●●●
　　●●　　
　　●●　　

　　●●　　
　　●●　　
□□●●●●
□□●●●●
　　●●　　
　　●●　　

　　●●　　
　　●●　　
●□□●●●
●□□●●●
　　●●　　
　　●●　　

　　●●　　
　　●●　　
●●□□●●
●●□□●●
　　●●　　
　　●●　　

　　●●　　
　　●●　　
●●●□□●
●●●□□●
　　●●　　
　　●●　　

　　●●　　
　　●●　　
●●●●□□
●●●●□□
　　●●　　
　　●●　　

　　●●　　
　　●●　　
●●●●●●
●●□□●●
　　□□　　
　　●●　　

　　●●　　
　　●●　　
●●●●●●
●●●●●●
　　□□　　
　　□□　　

　　●●　　
　　□●　　
●□●□●●
●●□●●●
　　●●　　
　　●●　　

　　●●　　
　　●□　　
●●□●□●
●●●□●●
　　●●　　
　　●●　　

　　●●　　
　　●●　　
●●□●●●
●□●□●●
　　□●　　
　　●●　　

　　●●　　
　　●●　　
●●●□●●
●●□●□●
　　●□　　
　　●●　　

　　●●　　
　　□●　　
●●●●□●
●□●●●●
　　●□　　
　　●●　　

　　●●　　
　　●□　　
●□●●●●
●●●●□●
　　□●　　
　　●●　　

　　□●　　
　　●●　　
□●●●□●
●●●●●●
　　□●　　
　　●●　　

　　●□　　
　　●●　　
●□●●●□
●●●●●●
　　●□　　
　　●●　　

　　●●　　
　　□●　　
●●●●●●
□●●●□●
　　●●　　
　　□●　　

　　●●　　
　　●□　　
●●●●●●
●□●●●□
　　●●　　
　　●□　　

　　□●　　
　　●●　　
●●●●●□
□●●●●●
　　●●　　
　　●□　　

　　●□　　
　　●●　　
□●●●●●
●●●●●□
　　●●　　
　　□●　　

取り除く石の個数の最小は6個と思われます。
形は以下の8通りではないでしょうか。
×印は石を取り除いた個所です。

　　●●　　
　　×●　　
×●×●●●
●●●●×●
　　●×　　
　　●×　　

　　●●　　
　　×●　　
××●●●●
●●●××●
　　●●　　
　　●×　　

　　●●　　
　　●×　　
●●●×●×
●×●●●●
　　×●　　
　　×●　　

　　●●　　
　　●×　　
●●●●××
●××●●●
　　●●　　
　　×●　　

　　×●　　
　　●●　　
●××●●●
●●●●××
　　●×　　
　　●●　　

　　×●　　
　　×●　　
●×●●●●
●●●×●×
　　●×　　
　　●●　　

　　●×　　
　　●×　　
●●●●×●
×●×●●●
　　×●　　
　　●●　　

　　●×　　
　　●●　　
●●●××●
××●●●●
　　×●　　
　　●●　　

　プログラムですべてのケースを調査した結果、6より少ない個数では不可能であることがわかりました。

【おまけ２】

【問題２】の解答に記述したように8通りと思います。

◆千葉県　菜花子 さんからの解答

　◆ 問題へもどる

　◆ 今週の問題へ

数学の部屋へもどる