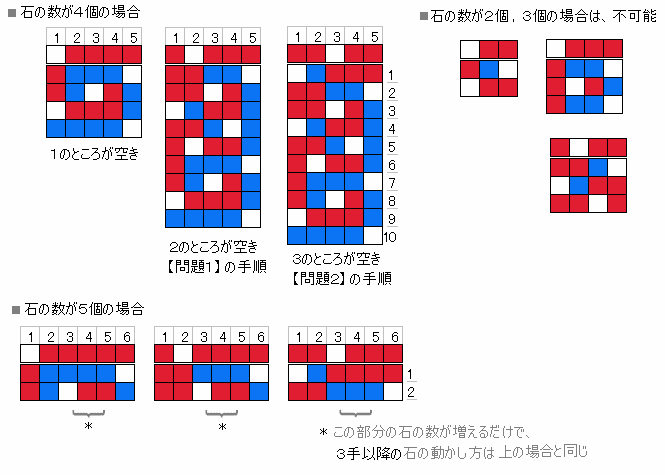
◆千葉県 菜花子 さんからの解答
【問題1】
9手
5→3→1→4→2→5→3→1→5→
【問題2】
10手
1→5→3→1→4→2→5→3→1→5→
(5→1→3→5→2→4→1→3→5→1→)
【おまけ1】
赤、青、空き、赤・・・(何個でも)、青、または、
青、赤・・・(何個でも)、青、赤、空き、
石が上のように並ぶまで移動を繰り返す。
【おまけ2】
石の数が4個以上であれば、一箇所の空きがどこであっても、全ての石を青色にすることは可能。

◆愛知県 Y.M.Ojisan さんからの解答。
【問題1】
9回
5→3→1→4→2→5→3→1→5
図1緑経路
【問題2】
10回
1→5→3→1→4→2→5→3→1→5
図1赤紫経路
【おまけ2】
可能
状態は全部で空き位置:5 こま状態:24の積で80通りある。
左右の対称性を考慮すると実質42通りあり、これらの状態遷移を列挙すると図1である。
◆図1
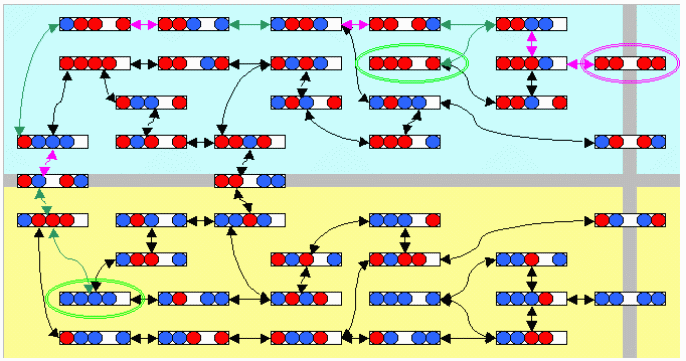
それら42状態は全て連絡しており、4個の場合、任意の状態から任意の状態に遷移可能である。
ただし左右状態の交換は●●〇●●または●●〇●●または●●〇●●または●●〇●●まで一度行く必要あり。
5個以上の場合,
(1)空きを端に移動(何時でも可能)
(2)空きを含む端の5マスに関する操作を行い、端を青にする。
(これも図1より何時でも可能)
(3)端の青を固定し、石の数が少ない場合に帰着。
により最終的に4個の問題に帰着できる。
1個、2個が常には可能でないことは明らか。
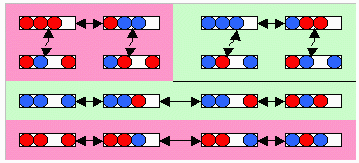
3個の時は図2であり、常にはできない。
◆図2
◆東京都 明 さんからの解答
【問題1】
5→3→1→4→2→5→3→1→5 (9手)
【問題2】
1→5→3→1→4→2→5→3→1→5 (10手)
【おまけ1】
【問題1】の配置(2番目が空き)に対し、基本操作として下記の2つの操作を定義します。
T:4→1→5→2
R:5→1→3→5→2
配置のn番目の石の状態をSnとすると上の操作は初期の状態を以下のように置換します。
T:(S1,×,S3,S4,S5) → (S5,×,S3,S1,S4)
R:(S1,×,S3,S4,S5) → (S3,×,-S1,S4,S5)
ただし、-SnはSnの裏返しを表します。
(すなわちTはS1,S4,S5の巡回置換、RはS1,S3の互換+S1の反転)
この2つの基本操作により、以下のように特定の指定された位置の石のみを裏返しにすることができます。
(操作後、石の位置は替わることに注意。)
-S1:R
-S3:RRR (前から順に操作を行う。)
-S4:TTR
-S5:TR
よって、操作後の石の位置に注意すると、2つの上記基本操作のみで任意に選ばれた石を裏返しにできます。
この2つの操作で【問題1】の石をすべて裏返しにする操作は下記のとおりです。
RRTRTR
5→1→3→5→2→5→1→3→5→2→
4→1→5→2→5→1→3→5→2→4→
1→5→2→5→1→3→5→2
【おまけ2】
【おまけ1】で、4つの石の場合、空きの位置がどこにあろうと多くとも2手以内で2番目の位置をに空きすることは可能です。
したがって4つの石の場合、どのような配置、裏表の状態でもすべて裏にすることができます。
石を1つ増やし5つにしたとき、どのような配置、裏表の状態でもどちらかの端の石を裏にすることは3手以内で可能です。
残りの4つの石はすべて裏にできるので、結局5つの石でどのような配置、裏表の状態でもすべてを裏にすることができます。
以下同じ考え方を続けることができるので、任意の数の任意の配置の石ですべて裏にすることが証明されました。
(数学的帰納法)
具体的に配置が与えられた場合は、右端の空きを含めた5つの配置を【おまけ1】の方法ですべて裏返しにし、次に空きの位置を左へ3つ移動し、元空きの位置から5つの配置を同様にしてすべて裏返しにするという操作を続ければ、具体的 な手順を求めることができます。
また、任意の配列からすべてを裏にすることができることと、転置の操作を逆にたどることができることを考えあわせると、任意の配列から別の任意の配列に変換することが可能であることが解ります。
その他、本問題を考える途中で気付いた事柄を報告します。
1.
このような置換問題はアミダに置き換えることができますが、アミダに置き換えたとき、各石の反転はアミダをたどったときに交差する横棒の数の偶奇で決まる。
(奇数の時、反転)・・・自明
2.
各石の反転は次の式の偶奇で決定される。
(奇数の時反転)
(1.の性質による)
該当の石の、移動後の配置の順位−元の配置の順位+移動後の、該当の石の順位と他の石の順位の転倒数(空きの位置の順位は除く)+該当の石の転置の回数
3.
全体の石の反転の偶奇は次の式の偶奇による。
(2.をすべての石について加えあわせる)
空きの位置の、移動後の配置の順位−元の配置の順位+全体の転置の回数
【問題1】では 空きの位置の順位の差=3
全体の転置の回数 =9
【問題2】では 空きの位置の順位の差=2
全体の転置の回数 =10
でいずれも偶数となっています。
以上のような方向から解へ到達できないか考えましたが、できませんでした。
◆広島県 清川 育男 さんからの解答
●最小回数と手順の予想
赤 1 青 2 4 個 0 1 1 1 1 5, 3, 1, 5, 4回 1 0 1 1 1 5, 3, 1, 4, 2, 5, 3, 1, 5, 9回 1 1 0 1 1 1, 5, 3, 1, 4, 2, 5, 3, 1, 5, 10回 ------------------------------------------- 5 個 0 1 1 1 1 1 6, 3, 1, 6, 4回 1 0 1 1 1 1 6, 3, 1, 6, 4, 2, 6, 7回 1 1 0 1 1 1 1, 6, 3, 1, 6, 4, 2, 6, 8回 ------------------------------------------- 6 個 0 1 1 1 1 1 1 7, 3, 1, 7, 4回 1 0 1 1 1 1 1 7, 3, 1, 7, 4, 2, 7, 7回 1 1 0 1 1 1 1 1, 7, 3, 1, 7, 4, 2, 7, 8回 1 1 1 0 1 1 1 1, 3, 6, 4, 7, 5, 1, 7回 ------------------------------------------- 7 個 0 1 1 1 1 1 1 1 8, 3, 1, 8, 4回 1 0 1 1 1 1 1 1 8, 3, 1, 8, 4, 2, 8, 7回 1 1 0 1 1 1 1 1 1, 8, 3, 1, 8, 4, 2, 8, 8回 1 1 1 0 1 1 1 1 8, 5, 2, 4, 1, 3, 8, 7回 ------------------------------------------- 8 個 0 1 1 1 1 1 1 1 1 9, 3, 1, 9, 4回 1 0 1 1 1 1 1 1 1 9, 3, 1, 9, 4, 2, 9, 7回 1 1 0 1 1 1 1 1 1 1, 9, 3, 1, 9, 4, 2, 9, 8回 1 1 1 0 1 1 1 1 1 9, 5, 2, 4, 1, 3, 9, 7回 1 1 1 1 0 1 1 1 1 1, 9, 5, 2, 4, 1, 3, 9, 8回 ------------------------------------------- 9 個 0 1 1 1 1 1 1 1 1 1 10, 3, 1,10, 4回 1 0 1 1 1 1 1 1 1 1 10, 3, 1,10, 4, 2,10, 7回 1 1 0 1 1 1 1 1 1 1 1,10, 3, 1,10, 4, 2,10, 8回 1 1 1 0 1 1 1 1 1 1 10, 5, 2, 4, 1, 3,10, 7回 1 1 1 1 0 1 1 1 1 1 1,10, 5, 2, 4, 1, 3,10, 8回 ------------------------------------------- 10 個 0 1 1 1 1 1 1 1 1 1 1 11, 3, 1,11, 4回 1 0 1 1 1 1 1 1 1 1 1 11, 3, 1,11, 4, 2,11, 7回 1 1 0 1 1 1 1 1 1 1 1 1,11, 3, 1,11, 4, 2,11, 8回 1 1 1 0 1 1 1 1 1 1 1 11, 5, 2, 4, 1, 3,11, 7回 1 1 1 1 0 1 1 1 1 1 1 1,11, 5, 2, 4, 1, 3,11, 8回 1 1 1 1 1 0 1 1 1 1 1 1,11, 6, 1, 4, 2, 5, 3,11, 9回 ------------------------------------------- 11 個 0 1 1 1 1 1 1 1 1 1 1 1 12, 3, 1,12, 4回 1 0 1 1 1 1 1 1 1 1 1 1 12, 3, 1,12, 4, 2,12, 7回 1 1 0 1 1 1 1 1 1 1 1 1 1,12, 3, 1,12, 4, 2,12, 8回 1 1 1 0 1 1 1 1 1 1 1 1 12, 5, 2, 4, 1, 3,12, 7回 1 1 1 1 0 1 1 1 1 1 1 1 1,12, 5, 2, 4, 1, 3,12, 8回 1 1 1 1 1 0 1 1 1 1 1 1 1,12, 6, 1, 4, 2, 5, 3,12, 9回 ------------------------------------------- 12 個 0 1 1 1 1 1 1 1 1 1 1 1 1 13, 3, 1,13, 4回 1 0 1 1 1 1 1 1 1 1 1 1 1 13, 3, 1,13, 4, 2,13, 7回 1 1 0 1 1 1 1 1 1 1 1 1 1 1,13, 3, 1,13, 4, 2,13, 8回 1 1 1 0 1 1 1 1 1 1 1 1 1 13, 5, 2, 4, 1, 3,13, 7回 1 1 1 1 0 1 1 1 1 1 1 1 1 1,13, 5, 2, 4, 1, 3,13, 8回 1 1 1 1 1 0 1 1 1 1 1 1 1 1,13, 6, 1, 4, 2, 5, 3,13, 9回 1 1 1 1 1 1 0 1 1 1 1 1 1 1,13, 7, 1, 6, 3, 5, 2, 4,13, 10回 ------------------------------------------- 13 個 0 1 1 1 1 1 1 1 1 1 1 1 1 1 14, 3, 1,14, 4回 1 0 1 1 1 1 1 1 1 1 1 1 1 1 14, 3, 1,14, 4, 2,14, 7回 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1,14, 3, 1,14, 4, 2,14, 8回 1 1 1 0 1 1 1 1 1 1 1 1 1 1 14, 5, 2, 4, 1, 3,14, 7回 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1,14, 5, 2, 4, 1, 3,14, 8回 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1,14, 6, 1, 4, 2, 5, 3,14, 9回 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1,14, 7, 1, 6, 3, 5, 2, 4,14, 10回 ------------------------------------------- 14 個 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 15, 3, 1,15, 4回 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 15, 3, 1,15, 4, 2,15, 7回 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1,15, 3, 1,15, 4, 2,15, 8回 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 15, 5, 2, 4, 1, 3,15, 7回 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1,15, 5, 2, 4, 1, 3,15, 8回 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1,15, 6, 1, 4, 2, 5, 3,15, 9回 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1,15, 7, 1, 6, 3, 5, 2, 4,15, 10回 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1,15, 8, 1, 7, 2, 5, 3, 6, 4,15, 11回 ------------------------------------------- 15 個 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 16, 3, 1,16, 4回 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 16, 3, 1,16, 4, 2,16, 7回 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1,16, 3, 1,16, 4, 2,16, 8回 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 16, 5, 2, 4, 1, 3,16, 7回 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1,16, 5, 2, 4, 1, 3,16, 8回 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1,16, 6, 1, 4, 2, 5, 3,16, 9回 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1,16, 7, 1, 6, 3, 5, 2, 4,16, 10回 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1,16, 8, 1, 7, 2, 5, 3, 6, 4,16, 11回 ------------------------------------------- 16 個 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 17, 3, 1,17, 4回 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 17, 3, 1,17, 4, 2,17, 7回 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1,17, 3, 1,17, 4, 2,17, 8回 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 17, 5, 2, 4, 1, 3,17, 7回 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1,17, 5, 2, 4, 1, 3,17, 8回 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1,17, 6, 1, 4, 2, 5, 3,17, 9回 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1,17, 7, 1, 6, 3, 5, 2, 4,17, 10回 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1,17, 8, 1, 7, 2, 5, 3, 6, 4,17, 11回 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1,17, 9, 1, 8, 2, 7, 4, 6, 3, 5,17, 12回
出来上がりを左詰めとする。
4個の場合は例外的とすれば、最短手順は1通りではありませんが、以下のパターンが規則性においてシンプルだと思います。
赤 1 青 2 4 個 0 1 1 1 1 5, 3, 1, 5, 4回 1 0 1 1 1 5, 3, 1, 4, 2, 5, 3, 1, 5, 9回 1 1 0 1 1 1, 5, 3, 1, 4, 2, 5, 3, 1, 5, 10回 ------------------------------------------- 5 個 0 1 1 1 1 1 6, 3, 1, 6, 4回 1 0 1 1 1 1 6, 3, 1, 6, 4, 2, 6, 7回 1 1 0 1 1 1 1, 6, 3, 1, 6, 4, 2, 6, 8回 ------------------------------------------- 6 個 0 1 1 1 1 1 1 7, 3, 1, 7, 4回 1 0 1 1 1 1 1 7, 3, 1, 7, 4, 2, 7, 7回 1 1 0 1 1 1 1 1, 7, 3, 1, 7, 4, 2, 7, 8回 1 1 1 0 1 1 1 7, 5, 1, 4, 2, 3, 7, 7回 ------------------------------------------- 7 個 0 1 1 1 1 1 1 1 8, 3, 1, 8, 4回 1 0 1 1 1 1 1 1 8, 3, 1, 8, 4, 2, 8, 7回 1 1 0 1 1 1 1 1 1, 8, 3, 1, 8, 4, 2, 8, 8回 1 1 1 0 1 1 1 1 8, 5, 1, 4, 2, 3, 8, 7回 ------------------------------------------- 8 個 0 1 1 1 1 1 1 1 1 9, 3, 1, 9, 4回 1 0 1 1 1 1 1 1 1 9, 3, 1, 9, 4, 2, 9, 7回 1 1 0 1 1 1 1 1 1 1, 9, 3, 1, 9, 4, 2, 9, 8回 1 1 1 0 1 1 1 1 1 9, 5, 1, 4, 2, 3, 9, 7回 1 1 1 1 0 1 1 1 1 1, 9, 5, 1, 4, 2, 3, 9, 8回 ------------------------------------------- 9 個 0 1 1 1 1 1 1 1 1 1 10, 3, 1,10, 4回 1 0 1 1 1 1 1 1 1 1 10, 3, 1,10, 4, 2,10, 7回 1 1 0 1 1 1 1 1 1 1 1,10, 3, 1,10, 4, 2,10, 8回 1 1 1 0 1 1 1 1 1 1 10, 5, 1, 4, 2, 3,10, 7回 1 1 1 1 0 1 1 1 1 1 1,10, 5, 1, 4, 2, 3,10, 8回 ------------------------------------------- 10 個 0 1 1 1 1 1 1 1 1 1 1 11, 3, 1,11, 4回 1 0 1 1 1 1 1 1 1 1 1 11, 3, 1,11, 4, 2,11, 7回 1 1 0 1 1 1 1 1 1 1 1 1,11, 3, 1,11, 4, 2,11, 8回 1 1 1 0 1 1 1 1 1 1 1 11, 5, 1, 4, 2, 3,11, 7回 1 1 1 1 0 1 1 1 1 1 1 1,11, 5, 1, 4, 2, 3,11, 8回 1 1 1 1 1 0 1 1 1 1 1 11, 7, 1, 6, 2, 5, 3, 4,11, 9回 ------------------------------------------- 11 個 0 1 1 1 1 1 1 1 1 1 1 1 12, 3, 1,12, 4回 1 0 1 1 1 1 1 1 1 1 1 1 12, 3, 1,12, 4, 2,12, 7回 1 1 0 1 1 1 1 1 1 1 1 1 1,12, 3, 1,12, 4, 2,12, 8回 1 1 1 0 1 1 1 1 1 1 1 1 12, 5, 1, 4, 2, 3,12, 7回 1 1 1 1 0 1 1 1 1 1 1 1 1,12, 5, 1, 4, 2, 3,12, 8回 1 1 1 1 1 0 1 1 1 1 1 1 12, 7, 1, 6, 2, 5, 3, 4,12, 9回 ------------------------------------------- 12 個 0 1 1 1 1 1 1 1 1 1 1 1 1 13, 3, 1,13, 4回 1 0 1 1 1 1 1 1 1 1 1 1 1 13, 3, 1,13, 4, 2,13, 7回 1 1 0 1 1 1 1 1 1 1 1 1 1 1,13, 3, 1,13, 4, 2,13, 8回 1 1 1 0 1 1 1 1 1 1 1 1 1 13, 5, 1, 4, 2, 3,13, 7回 1 1 1 1 0 1 1 1 1 1 1 1 1 1,13, 5, 1, 4, 2, 3,13, 8回 1 1 1 1 1 0 1 1 1 1 1 1 1 13, 7, 1, 6, 2, 5, 3, 4,13, 9回 1 1 1 1 1 1 0 1 1 1 1 1 1 1,13, 7, 1, 6, 2, 5, 3, 4,13, 10回 ------------------------------------------- 13 個 0 1 1 1 1 1 1 1 1 1 1 1 1 1 14, 3, 1,14, 4回 1 0 1 1 1 1 1 1 1 1 1 1 1 1 14, 3, 1,14, 4, 2,14, 7回 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1,14, 3, 1,14, 4, 2,14, 8回 1 1 1 0 1 1 1 1 1 1 1 1 1 1 14, 5, 1, 4, 2, 3,14, 7回 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1,14, 5, 1, 4, 2, 3,14, 8回 1 1 1 1 1 0 1 1 1 1 1 1 1 1 14, 7, 1, 6, 2, 5, 3, 4,14, 9回 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1,14, 7, 1, 6, 2, 5, 3, 4,14, 10回 ------------------------------------------- 14 個 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 15, 3, 1,15, 4回 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 15, 3, 1,15, 4, 2,15, 7回 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1,15, 3, 1,15, 4, 2,15, 8回 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 15, 5, 1, 4, 2, 3,15, 7回 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1,15, 5, 1, 4, 2, 3,15, 8回 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 15, 7, 1, 6, 2, 5, 3, 4,15, 9回 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1,15, 7, 1, 6, 2, 5, 3, 4,15, 10回 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 15, 9, 1, 8, 2, 7, 3, 6, 4, 5,15, 11回 ------------------------------------------- 15 個 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 16, 3, 1,16, 4回 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 16, 3, 1,16, 4, 2,16, 7回 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1,16, 3, 1,16, 4, 2,16, 8回 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 16, 5, 1, 4, 2, 3,16, 7回 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1,16, 5, 1, 4, 2, 3,16, 8回 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 16, 7, 1, 6, 2, 5, 3, 4,16, 9回 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1,16, 7, 1, 6, 2, 5, 3, 4,16, 10回 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 16, 9, 1, 8, 2, 7, 3, 6, 4, 5,16, 11回 ------------------------------------------- 16 個 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 17, 3, 1,17, 4回 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 17, 3, 1,17, 4, 2,17, 7回 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1,17, 3, 1,17, 4, 2,17, 8回 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 17, 5, 1, 4, 2, 3,17, 7回 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1,17, 5, 1, 4, 2, 3,17, 8回 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 17, 7, 1, 6, 2, 5, 3, 4,17, 9回 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1,17, 7, 1, 6, 2, 5, 3, 4,17, 10回 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 17, 9, 1, 8, 2, 7, 3, 6, 4, 5,17, 11回 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1,17, 9, 1, 8, 2, 7, 3, 6, 4, 5,17, 12回 ------------------------------------------- 17 個 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 18, 3, 1,18, 4回 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 18, 3, 1,18, 4, 2,18, 7回 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1,18, 3, 1,18, 4, 2,18, 8回 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 18, 5, 1, 4, 2, 3,18, 7回 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1,18, 5, 1, 4, 2, 3,18, 8回 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 18, 7, 1, 6, 2, 5, 3, 4,18, 9回 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1,18, 7, 1, 6, 2, 5, 3, 4,18, 10回 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 18, 9, 1, 8, 2, 7, 3, 6, 4, 5,18, 11回 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1,18, 9, 1, 8, 2, 7, 3, 6, 4, 5,18, 12回
プログラムでは最小手順の1例を表現することが出来ました。
24 個 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 25, 3, 1,25, 4回 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 25, 3, 1,25, 4, 2,25, 7回 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1,25, 3, 1,25, 4, 2,25, 8回 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 25, 5, 1, 4, 2, 3,25, 7回 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1,25, 5, 1, 4, 2, 3,25, 8回 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 25, 7, 1, 6, 2, 5, 3, 4,25, 9回 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1,25, 7, 1, 6, 2, 5, 3, 4,25, 10回 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 25, 9, 1, 8, 2, 7, 3, 6, 4, 5,25, 11回 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1,25, 9, 1, 8, 2, 7, 3, 6, 4, 5,25, 12回 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 25,11, 1,10, 2, 9, 3, 8, 4, 7, 5, 6,25, 13回 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1,25,11, 1,10, 2, 9, 3, 8, 4, 7, 5, 6,25, 14回 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 25,13, 1,12, 2,11, 3,10, 4, 9, 5, 8, 6, 7,25, 15回 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1,25,13, 1,12, 2,11, 3,10, 4, 9, 5, 8, 6, 7,25, 16回 ------------------------------------------- 25 個 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 26, 3, 1,26, 4回 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 26, 3, 1,26, 4, 2,26, 7回 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1,26, 3, 1,26, 4, 2,26, 8回 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 26, 5, 1, 4, 2, 3,26, 7回 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1,26, 5, 1, 4, 2, 3,26, 8回 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 26, 7, 1, 6, 2, 5, 3, 4,26, 9回 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1,26, 7, 1, 6, 2, 5, 3, 4,26, 10回 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 26, 9, 1, 8, 2, 7, 3, 6, 4, 5,26, 11回 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1,26, 9, 1, 8, 2, 7, 3, 6, 4, 5,26, 12回 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 26,11, 1,10, 2, 9, 3, 8, 4, 7, 5, 6,26, 13回 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1,26,11, 1,10, 2, 9, 3, 8, 4, 7, 5, 6,26, 14回 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 26,13, 1,12, 2,11, 3,10, 4, 9, 5, 8, 6, 7,26, 15回 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1,26,13, 1,12, 2,11, 3,10, 4, 9, 5, 8, 6, 7,26, 16回
◆ 問題へもどる
◆ 今週の問題へ