◆東京都 明 さんからの解答
【問題1】
できます。
(1,8)→(2,7)→(3,8)→(2,9)→(4,9)→
(5,8)→(4,7)→(3,10)→(3,6)
【問題2】
できません。
2段目までを赤にすると下記のようなパターンになります。
(○:赤 ×:青 とします。)
パターン1
○ ○ ○ × × × ○ × × ○ ○ ○ ○ ○ ○3段目を赤にするためには4段目の青を下ろさなければならず、 下ろしたときのパターンは下記のとおりです。
パターン2
○ ○ ○ × × × ○ ○ ○ ○ ○ × × × ○ ○ ○ × × ○ ○ ○ ○ ○ ○ ○ ○ ○すなわちパターン1の3段目、4段目の形が5段目、6段目に現れます。
この状態から3段目の3個の石を下ろすためには5段目の3個の石をおろさなければなりません。
これは3段目と同じ状況が5段目に発生することになり、以下同じことが繰り返されることになります。
以上により、少なくとも有限回の手順で、3段目のまでのすべての石を赤にすることはできないことが証明されました。
【おまけ1】
任意のn個を選んだとき、そのn個すべてを赤にすることができ、特定のn+1個を選んだとき、どのように操作しても少なくとも1つは赤にできないようなnが存在するとします。
(nが1の時は明らかにどのような石でも赤にでき、またn+1が6の時は【問題2】によりすべてを赤にできないような石の配置があることから、1≦n≦5のnが存在します。)
以下すべてを赤にできないようなn+1個の配置(便宜上「不可配置」と呼びます。)を探すことを考えます。
(1)不可配置は1段目の石を含みます。
含まない配置は初期状態ではすべて赤です。
(2)不可配置は2段目の石の少なくとも1個を含みます。
2個とも含まない配置は1段目の石を下ろしたときすべて赤となります。
(3)不可配置は2段目の石2個共を含みます。
もし含まないとした場合、次のようなパターンが許されます。
○ ? × ? ? ○ ? ? ? ○ ? ? ? ? ○(×の位置が不可配置に含まれない石とします。)
すると、「?」で出来た集合は初期状態の石の集合と全く同じ条件です。
したがって任意のn個を選択しても、すべてを赤にすることができます。
これは(1)の石を含めn+1個となるにもかかわらず、すべてを赤にできることになり、不可配置の条件を満たせません。
以上により、1段目、2段目の合計3個の石は不可配置に必須です。
1段目、2段目の石を赤にすると【問題2】のパターン1となります。
(4)ここで不可配置は3段目の3個の石の少なくとも1個の石を含むことを証明します。
もし含まないとすると次のようなパターンが許されます。
○ ○ ○ × × × ○ ? ? ○ ○ ? ? ? ○ ○ ? ? ? ? ○「?」で出来た集合は、頂点の「×」を除けば、初期状態の石の集合で1段目の石を下ろしたものと同じものです。
これは不可配置に必須の上記3個の石を含めn+2個となるにもかかわらずすべてを赤にできることになり、不可配置の条件を満たせません。
次に上記の不可配置に必要な4個の石を選択した場合、4個だけではすべてを赤にできることを確認します。
具体的には下記のとおりです。
(パターン2からの操作になっています。)
○ ○ ○ ○ × × × × ○ ○ ○ × × × ○ ○ ○ × × ○ ○ ○ ○ ○ × ○ × ○ × × ○ ○ × × × ○ ○ ○ × × ○ ○ ○ ○ ○ × × ○ ○ ○ × × ○ × × × ○ ○ ○ × × ○ ○上記以外の4個を選択した場合は上で議論したようにすべて赤とすることができます。
以上により4個の石を任意に選択しても、すべての石を赤とできることが証明できました。
【おまけ2】
【問題2】でパターン2から3段目の3個の石を下ろすことができないことを示しましたが、この議論は3段目の隣り合った2個の石を下ろす場合でも全く同様に適用できます。
このことから下記が不可配置となります。
(□が不可配置です。)
□ □ □ ○ □ □ ○ ○ ○ ○ □ □ □ □ □ ○ ○ ○ ○ ○またパターン2の3段目の両端2個の石を選ぶ場合、および3段目の1個の石と5,6段目5個の「×」の石から1個の計2個を選ぶ場合は、すべてを赤にすることが確かめられます。
【おまけ3】
パスカルの3角形と同じように、頂点に1を置き、石が選択されていればすぐ下の2つの石の位置に上の石の値を加えて行く操作を上から順におこないます。
すべての石が選択されていれば以下のとおりです。
1 1 1 1 2 1 1 3 3 1選択されていない石は、それが0でない時、1を引いてすぐ下の2つの石の位置に加えます。
選択された石が下記の□のようであれば、その下のような数列となります。
□ □ □ □ ○ □ ○ ○ ○ ○ 1 1 1 1 2 1 1 2 2 1 0 1 2 1 0 0 0 1 1 0 0 0 0 0 0 0 0 0一連の操作後の結果は、この数列で0の部分と選択された石が赤となり、それ以外の石が青という配列になります。
下記不可配置の場合はその下の数列となります。
□ □ □ ○ □ □ ○ ○ ○ ○ 1 1 1 1 2 1 0 2 3 1数列の中に3ができるような操作はできないことを示すことができます。
証明は【問題2】と同じような方法でできます。
すなわち3以上の値ができると、その隣のいずれかは2以上であり、以下の石がすべて選択されていない場合でも、3以上と2以上の値の並びが下方向へ無限に続くことになります。
これは有限回で操作を完了できないことを示します。
以上のことから、上記方法で上から順に数列を作り、すべて2以下の数列となれば、有限回で0となり、選択された石をすべて赤にできます。
(選択した石が無限にあれば有限回で0にならない場合がありますが、この場合でも上から順に石を下ろす操作を無限に続けることはできます。)
途中で3以上ができれば選択した石のいずれかが青として残ることになります。
◆愛知県 Y.M.Ojisan さんからの解答。
【問題1】
(1,8)→(2,7)→(3,8)→(2,9)→(4,7)→
(3,6)→(5,8)→(4,9)→(3,10)
【問題2】
不可能 おまけ3参照
【おまけ1】
(1)頂点が4個の中に入っていなければ既に成立
(2)頂点が4個の中に入り残り3個は3段目以下のときは1回の操作で成立
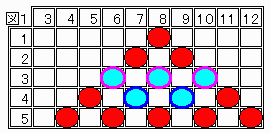
(3)頂点および2段目の2個が4個の中に入り、残り1個が図1の紫枠/青枠のもの以外では4回の操作で成立。
また紫枠のものどちらか一方は後一回で赤にすることができる。

紫枠のもの3個のいずれかは図2のように、3回の操作で青枠のものを移動させた後、赤にすることができる。
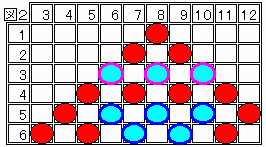
(4)頂点および2段目の1個が4個の中に入り、残り2個が図3の紫枠のもの以外では2回の操作で成立。
また紫枠のもの両方を赤にすることは、図1から図2へで行った操作(3回)で可能。
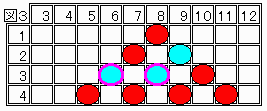
紫枠のものの一方だけでよい場合は次の図4になり、後一回の操作で青枠のものの一方を赤に変えることが可能。
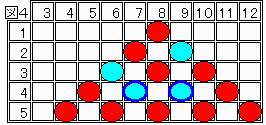
以上(1)-(4)により任意の4個を赤にできることが示された。
【おまけ2】
ある。下図5の赤の配置
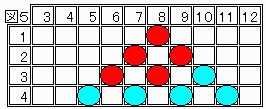
【おまけ3】
セルに通過する〇の数を書き込む。
これはパスカルの三角形に似ている。
ただし少し違うのは、先に進まない(青)ことにより最大1引いてもよいことである。
逆に先に進んで赤にする場合はパスカル三角そのものである。
すると、セル値=2以上 と セル値=1以上が隣接する場合は、解答が無いことを意味する。
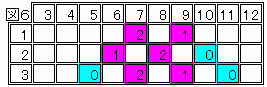
∵ 図6に示すように2段目においても セル値=1とセル値=2が隣接し、これらから再び3段目においても同様であり、操作が終了できない状態になるからである。
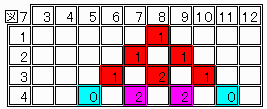
問題2の場合を見てみると、3段目までは1を引くことができず、3段目に2と1の隣接が現れるので不可能であることが分かる。
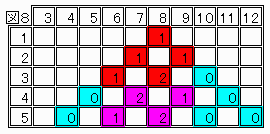
おまけ2の場合を図8に示す。
隣接2−1の繰り返しに陥る。
まとめると、
|
空けるところはパスカルの三角形の計算、 そうでない所はパスカルの三角形の計算−1を順次行って行き、 値に2と1以上の隣接が現れたら不可能。 有限段で全部0に成ったら可能。 |
◆ 問題へもどる
◆ 今週の問題へ