�����m���@Y.M.Ojisan ����̉B
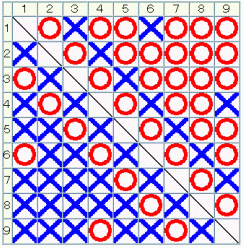
�y���P�z

�y���Q�z
�R�l����A,B,C�N���X�ɕ���
�i�P�j �N���X���ł͂R�����݁i�܂�e�l�P���j
�i�Q�j �`�͂a����e�l�Q���A�b����e�l�R�����S�U�����b����R��
�i�R�j �a�͂b����e�l�Q���@���S�S�����b����Q���@���@�b�͑S�Q�����b����P��
����������n�j�D���ې��������B
�y���R�z�@�X�l�̂�
�b�N���X���ł͂R��������A���������v�͂R�ł���B
����Ăb�N���X�̂R�l�̏��������v�͂��̔{�̂U�Ɍ�����B
������ϓ��ɕ�����Ƃ��Ă��Œ�b�N���X�̐l�̏������͂Q�ł���B
����Ă`�`�a�N���X�̐l�̏������͂S���U�i�b�N���X�͂R�l�j�łȂ���Ȃ�Ȃ��B
�l�����m�Ƃ���Ƃ��A�g�[�i�����g�S�̂̏��������m�b�Q�ł��肱�̐��ɂ͎��̏��������Ȃ���Ȃ�Ȃ��B
�i�P�j �����ł���B
�i�Q�j �S�i�m�|�R�j�{�U�ȏ�
�i�R�j �U�i�m�|�R�j�{�U�ȉ�
�ȏ������m�͂W�ƂX�����ł���B
�m���X�́y���P�z�ő��݂��m�F����Ă���B
�m���W�̏ꍇ�A�������Q�W��U�蕪����Ƃ`�N���X�P�l�A�a�N���X�S�l�y�тb�N���X�R�l�łȂ���Ȃ�Ȃ��B
�a�N���X�͂b�N���X�Ɋe�l�P�s�F�S�̂łS�s���Ȃ���Ȃ�Ȃ��B
����A�b�N���X�͂`�N���X�ɂ͏��ĂȂ��̂ła�N���X���璚�x���v�R�����Ȃ���Ȃ炸��������B
����Ăm���W�͕s�\�B
�y�o�B�r�B�z
�������^�C���͓����_���Ƃ��g�X�ŏ��ʂ����߂�ꍇ�́A���́y���P�z�̉�������B�_�~�~������������
���_�~�����~������
�����_�~���~������
�~�~���_�~���~����
�~�~�~���_���~����
�~�����~�~�_���~��
�~�~�~�����~�_����
�~�~�~�~�~���~�_��
�~�~�~�~�~�~�~�~�_
���̏ꍇ�A���R�̏����i�Q�j�͂Q�i�m�|�R�j�{�U�ȏ�ł���B
�����Ăm���T��������������̂Ƃ��ĉ����B
�����@�b�N���X�T�l�ł���B
���������̉��͑��݂��Ȃ��B
�܂��m���W�̏ꍇ�A�V�����N���X�������\�ɂȂ�B
�����@�c�N���X�O�����܂߂`�R�b�T�A�`�Q�a�Q�b�S�A�`�P�a�T�b�P�c�P�̂R�P�[�X���\������ɂȂ�B
�����������ɑΉ�����������݂��Ȃ��B
�]���Ă�͂�X�l�݂̂ł���B
�y�o�B�r�B�P�[�X�s�\�ؖ��P�z
���ʂR�`�[���͏�ʃ`�[������K�����v�R���������Ȃ���Ȃ�Ȃ��B
����͂a�܂��͂b�N���X����݂̂ł���B
�]���ď�ʃ`�[���̃N���X�����͂`X�a�P�b�P���`X�a�R�����Ȃ��B
�ia�j�m���T�̂b�T�̏�ʂ͂b�Q�ł���K�����Ȃ��B
�ib�j�m���W�̂`�R�b�T�̏�ʂ͂`�R�b�Q�ł���K�����Ȃ��B
�ic�j�m���W�̂`�Q�a�Q�b�S�̏�ʂ͂`�Q�a�Q�b�P�ł���K�����Ȃ��B
�id�j�m���W�̂`�P�a�T�b�P�c�P�̏�ʂ͂`�P�a�S�ł���K�����Ȃ��B
�Ȃ��A (���R��) �m���W�̂`�P�a�S�b�R�̏�ʂ͂`�P�a�S�ł���K�����Ȃ��B
�y�o�B�r�B�P�[�X�s�\�ؖ��Q�z
�@��ʂ�
(I) �m���mA+�mB+�mC+�mD
(II) �m�i�m�|�P�j�^�Q��6�mA+4�mB+2�mC
(III) �mB+2(�mC -3)=3 (���ʂb�R�P�[�X)�@
or�@�mB +2(�mC -1)=3 (����B1C1D1�P�[�X)
�ł�������mA,�mB,�mC,�mD�����邩�Ƃ������ɂ��Ȃ�܂��B
(III)����
[�mB���P�@�mC ���S �mD���O],
[�mB���R�@�mC���R �mD���O],
[�mB���P�@�mC���Q �mD���P],
[�mB���R�@�mC���P�@�mD���P]
�̂S�P�[�X���\�Ł@
4�mB+2�mC���P�Q�A�P�W�A�W�A�P�S��0 or 2 mod 6�@�ł��B
���Ȃ킿(II)�����@
�m�i�m�|�P�j�^�Q��0 or 2 mod 6�łȂ���Ȃ�܂���B
����Ăm���T�C�W�͐������܂���B
����m���X�͌��ł��B
���邢�́A(I)��������Ɓ@�@
�m�i�m�|�P�j/2���U�m�|[18|18|16|16] �ɋA������A
��������m���S�C�X�������܂��B
�m���S�͂mA���O�ŕs�K���ł��B
����Ăm���X�̂݁B
�������s�@���@����̉�
�y���P�z�_�~�����~�~�~�~�~
���_�~�~���~�~�~�~
�~���_�~�~���~�~�~
�~�����_�����~�~�~
���~���~�_�����~�~
�����~�~�~�_�����~
���������~�~�_����
�����������~�~�_��
�������������~�~�_
�y���Q�z
�u�S�������[�O��̍ʼn��ʂ���R�l�܂ł̑I��Ƃ̑ΐ�ŏ������̂��傤�ǔ������v���Ƃ���u�ʼn��ʂ���R�l�܂ł̕������v���S�̂̏����̔����ɂȂ�B
�X�l�̃��[�O��̂��߁A�S�̂̏����́@36
�R�l�̑��������́@24
���������āA�ʼn��ʂ���R�l�܂ł̑������� w �Ƃ���ƁA
2�(24-w) = 36
����� �@w = 6
�ʼn��ʂR�l�̌X�̏������ł��邾�����Ȃ����邽�߂ɂ́A�ʼn��ʂR�l���m�̐킢�͂R�����݁i�e���ꏟ���j���]�܂����B
�t�ɂP�l���Q�����Ă��܂��ƁA���̑I��͑�ӂ��S�����Ă��Ȃ���Ȃ炸�A �������ʂ̂U�I��͂T���ȏサ�Ă��Ȃ���Ȃ�Ȃ��B
�e�l�̏����́A�ʼn��ʂR�I�肩��̏����̔{�ł��邱�Ƃ�������łȂ��Ă͂Ȃ�Ȃ��B
���������ď�ʂU�I��́A���Ȃ��Ƃ��U���������Ă��邱�ƂɂȂ�A�S�̂̏�����36���z���Ă��܂��B
���������čʼn��ʂR�l�̐킢�͂R�����݂ƂȂ�Ȃ��Ă͂Ȃ�Ȃ��B
�ȏ���ʼn��ʂR�I��̌X�̏����͂Q�����ƂȂ�B
���̏����ʼn��ʂR�I��̏��s�����肷��B
���̂Ƃ����ʑI�肪����̏�ʑI�肩�珟�������Ȃ��悤�ɔz�u����B
�ʼn��ʂR�I��̏��s�����߂�ƁA��ʑI��U�l���ʼn��ʂR�I�肩���鏟�������܂�B
��͂��̏����Ɠ����������Ƃ��悤�ɁA��ʂU�l���m�̏��s�����肷��悢�B
�Ȃ��A�ʼn��ʂR�I��ɂ��Ă͏������ʼn��ʑI�蓯�m�̑ΐ�̏����̔{�ł��鐧�����O���ƁA�ȉ��̂悤�ȏ��s�\���\�ł����A��ӂɂ͍���Ȃ��悤�ł��B�_���~�~�~�~�~�~�~
�~�_�����~�~�~�~�~
���~�_�~�����~�~�~
���~���_�����~�~�~
�����~�~�_�����~�~
�����~�~�~�_�����~
���������~�~�_����
�����������~�~�_��
�������������~�~�_
�y���R�z
�ʼn��ʂR�I�蓯�m�̎������O���āA�ʼn��ʂR�I��Ə�ʂU�I���18�����̏��s�ɒ��ڂ���ƁA�ʼn��ʂ���R�l�܂ł̑����� w �ƑS�̂̏����Ƃ̊Ԃňȉ��̊W�����藧�B
�@2�(18-(w-3))+w = 36
�iw ���������� 3 �͍ʼn��ʓ��m�̎����̏����j
�����́y���Q�z�Ɠ������@w = 6
�i���ꂪ��L�u�ʼn��ʂR�I��ɂ��Ă͏������ʼn��ʑI�蓯�m�̑ΐ�̏����̔{�ł��鐧�����O���v�Ƃ��̏��s�\���\�ȗ��R�̈�ł��B�j
�ȏ�̍l��������A���[�O��ւ̎Q���l���� n �Ƃ���ƈȉ��̓��������邱�ƂɂȂ�B
2�(3�(n-1)-w) = n(n-1)/2 (1)
2�(3�(n-3)-(w-3))+w = n(n-1)/2 (2)
(2)-(1)��� n �ɂ�����炸
�@�@w = 6
(1)���ɑ������
n(n-1)/2-12�(n-1)+24 = 0
����� n2-13n+36 = 0
n = 9 �܂��� 4
n = 4 �̂Ƃ��͏��s�\�����L�̂悤�ɂȂ�A��ʑI�肪���݂��Ȃ��B�_���~��
�~�_����
���~�_��
�~�~�~�_
���������čʼn��ʂR�I���ΏۂƂ���ꍇ�A n = 9 �݂̂��������݂�����B
�ʼn��ʂ̑I����R�I�肩�� p �I��Ɋg������ƁA(1),(2)���͎��̂悤�ɕ\������܂��B
2�(p(n-1)-w) = n(n-1)/2 (1)
2�(p(n-p)-(w-p(p-1)/2))+w = n(n-1)/2 (2)
�����悤��(2)-(1)���� w �����߂�ƁA
�@�@w = p(p-1)
(1)�ɑ������ p �ɂ��ĉ�����
2p2-2np+n(n-1)/2 = 0
p = (n�}��n)/2
p �������ƂȂ邽�߂ɂ� n = k2 �̌`���K�v�ł���A�܂��ʼn��ʑI�萔���S�̂̔����ȉ��ł���ƍl����ƁA
p = k(k-1)/2�@ (n = k2)
�y���P�z�� k = 3�ɑΉ����Ă���B
k = 4 �Ƃ���ƂP�U�I��̃��[�O����������ƂɂȂ�A���̎��A�u�S�������[�O��̍ʼn��ʂ���U�l�܂ł̑I��Ƃ̑ΐ�ŏ������̂��傤�ǔ�����v�Ƃ��������ɂȂ�܂��B
���ۂ��̎��͈ȉ��̏��s�\�������ɍ��v���܂��B
�_�������~�~�@�������~�~�~�~�~�~�~
�~�_�������~�@�~�~�~�������~�~�~�~
�~�~�_�������@�~�~�~�~�~�~�������~
�~�~�~�_�����@���~�~�~�~�~�~�~�~��
���~�~�~�_���@�~�����~�~�~�~�~�~�~
�����~�~�~�_�@�~�~�~�����~�~�~�~�~
�~�����~�����@�_���������~�~�~�~�~
�~�������~���@�~�_���������~�~�~�~
�~�������~���@�~�~�_���������~�~�~
���~�������~�@�~�~�~�_���������~�~
���~�������~�@�~�~�~�~�_���������~
���~���������@���~�~�~�~�_��������
�����~�������@�����~�~�~�~�_������
�����~�������@�������~�~�~�~�_����
�����~�������@���������~�~�~�~�_��
�������~�����@�����������~�~�~�~�_
�i�ŏ��̂U�I�肪�ʼn��ʃO���[�v�ł��B�j
n = k2 (k��2) ���ׂĂŐ������邱�Ƃ͏ؖ��ł��Ă��܂��A���Ƃ��Ȃ肻���ȕ��͋C�ł��B
���Ȃ݂� n = 4 �͍ʼn��ʑI�肪�P���̑S�s�ŏ�� n = 4 �̕\�̂Ђ�����Ԃ��̌`�ɂȂ�܂��B
�����Q���@�j�T�@����̉�
���Ƃ��A�_�������~�~������
�~�_�������~������
�~�~�_������������
�~�~�~�_���������~
���~�~�~�_�����~��
�����~�~�~�_�~����
�~�~�~�~�~���_�~��
�~�~�~�~���~���_�~
�~�~�~���~�~�~���_
���̂悤�Ȋ����ɂȂ�܂��B
�������́A�S�������[�O��̍ʼn��ʂ���R�l�܂ł̑I��Ƃ̑ΐ�ŏ������̂��傤�ǔ������킯������S���������͋����ɂȂ�A�܂��ō��͂U���ɂȂ�B
�܂��A���[�O��̕\����S���̏������̍��v�͂R�U�ƂȂ邩��A�X�l�őg�ݍ��킹���l����ƁA�U�����R�l�A�S�����R�l�A�Q�����R�l�ƂȂ�A�ʼn��ʂ���R�l�Ƃ����̂́A���̂R�l�S�����Q�������Ă��邱�ƂɂȂ�B
�����ɒ��ڂ���ƁA���̂R�l�͂��݂��ɂP�������Ďc��̂P�����A���̂R�l�ȊO�̐l���炠���Ă��邱�ƂɂȂ�B
���l�ɍl���āA�S�������R�l�͍ʼn��ʂ̂R�l����Q�������A��ʂR�l�͍ʼn��ʂR�l�ɑS�����Ă��邱�ƂɂȂ�B
���̂悤�ɍl���ā��~�Ă͂߂Ă����ƁA���Ƃ͉��ʂ���̑g�ݍ��킹���ł���B
���R�́A�ʼn��ʂ̂R�l����ō��������鐯���́A�S���ɏ������Ƃ��̂R��������A���l�Q�����悤����ʂ͍ō��U���܂ł����ł��Ȃ��B
�܂��A��蕶�̏�������ʼn��ʂ̂R�l�͂��݂��ɂP�������ă��[�O�łQ���Ƃ����`�����ł��Ȃ��B
���������āA�Q���R�l�A�S���A�U�������l�����邩�Ƃ����g�ݍ��킹�ɂȂ�B
�P�O�l�A�P�P�l�̂Ƃ��̓��[�O��̑�����������ɂȂ��l��l�̏������������ł��邩��A���̑g�ݍ��킹���ł��Ȃ��B�P�Q�l�̂Ƃ��͍ʼn��ʂR�l���S�����Ďc��X�l���U������Ώ������͈�v���邪�A�ʼn��ʂR�l�����݂�����Q�������邱�Ƃ͕s�\�ł��邩��P�Q�l�������ł���B
���������āA�܂��ō��X�l�ł���Ƃ�����B
���ɁA�W�l�̂Ƃ��͂Q���R�l�A�S���S�l�A�U���P�l�A�V�l�A�U�l�͑�����������A�T�l�̂Ƃ��͂Q���R�l�Ŏc��Q�l�łS��������S���Q���Ƃ������ƂɂȂ�A�s�\�B
����ȉ��͂Ȃ��B
�W�l�̂Ƃ��͂S�����S�l�ɂȂ邪����ł͂Q�����R�l�łȂ��Ȃ�A���ǂ�����s�\�B
���������Ă��̖��ł͂X�l�݂̂ł���B
�����{�@Non�@����̉�
�y���P�z
�_���~�����~������
�~�_���~����������
���~�_���~��������
�~���~�_���~�����~
�~�~���~�_���~����
���~�~���~�_���~��
�~�~�~�~���~�_���~
�~�~�~�~�~���~�_��
�~�~�~���~�~���~�_
�y���Q�z
�X�l����ʂR�l(A�O���[�v),���ʂR�l(B�O���[�v),���ʂR�l(C�O���[�v)�ɕ����A
A-A �P���P�s�@A-B �Q���P�s�@A-C �R���O�s�@�i���������U�A��C�������R�j
B-A �P���Q�s�@B-B �P���P�s�@B-C �Q���P�s�@�i���������S�A��C�������Q�j
C-A �O���R�s�@C-B �P���Q�s�@C-C �P���P�s�@�i���������Q�A��C�������P�j
�Ƃ���Ə��������B�e�O���[�v���ł͎O�b�̏�ԁB
�i���������`�͂��ꂾ���ł͂Ȃ����j
�y���R�z
���ʂR�l��C�O���[�v�Ƃ�Ԃ��Ƃɂ���ƁA�������̐��́A
�E���������O�i��C�������O�j
�E���������Q�i��C�������P�j
�E���������S�i��C�������Q�j
�E���������U�i��C�������R�j
�̂S�̉\�����l������B
C�O���[�v���ΐ�i�����������R�j�ɂ��čl����B
�������������O�̑I�肪�����Ɖ��肷��ƁA
C�O���[�v�̍\���́A
�E���������O�i�O���[�v���������O�j
�E���������Q�i�O���[�v���������P�j...(A)
�E���������S�i�O���[�v���������Q�j...(B)
�̂R�l�Ƃ������ƂɂȂ�A���̑I��͂��ׂ�
�E���������U�i��C�O���[�v�������R�j
�Ƃ������ƂɂȂ邪�A���������C�O���[�v�I��̓O���[�v�O�I��ɑS�����ĂȂ����ƂɂȂ�A(A)��(B)�ɖ�������B
����āA���������O�̑I��͂��Ȃ��B
����āAC�O���[�v�̍\���́A
�E���������Q�i��C�������P�j
���R�l�Ƃ������ƂɂȂ�B
���̂Ƃ��AC�O���[�v�I��͂��ꂼ��O���[�v�O�I�肩��P���������Ă��邱�ƂɂȂ邪�A���̑I��͏d�Ȃ�Ȃ��B
�i�����d�Ȃ�Ƃ�����̑����C�O���[�v����ɍ��X�P�������ł��Ȃ����ƂɂȂ薵���j
����āAC�O���[�v�I��ɕ������I��
�E���������S�i��C�O���[�v�������Q�j
���R�l�B
�c�肪�A
�E���������U�i��C�O���[�v�������R�j
�Ƃ������ƂɂȂ�B
�I��̑��l����n�l�Ƃ���A���̓���́A
�E���������Q�@�R�l
�E���������S�@�R�l
�E���������U�@(n-6)�l
�ƂȂ�A�������̑����́A6+12+6(n-6)=6n-18�����A
���ΐ퐔���l����ƁA�������̑�����n(n-1)/2�ƂȂ�̂�
6n-18=n(n-1)/2�������āAn=4,9
���̂��������ɓK����̂͂X�l�̎��̂݁B
�������s�@��������@����̉�
�y���P�z�_�~�������~������
���_�~���~��������
�~���_�~����������
�~�~���_�~�������~
�~���~���_�~���~��
���~�~�~���_�~����
�~�~�~�~�~���_�~��
�~�~�~�~���~���_�~
�~�~�~���~�~�~���_
�y���Q�z
�`�@�b�a
�@�@�b
�|�|�{�|
�b�@�b�c�}�̂悤�ɑΐ�\�̊e�̈�ɂ`�`�c�Ɩ��O������B
�c�͉��ʂR�l�̒��ł̑ΐ�B�S�R��B
�c���ɂ́����R����A�Œ�P������l������B
��ӂ���A�b���́��̐��Ƃc���́��̐��͓����B
�b���������R�ƂȂ�B
�ΐ�\�̓�������A�a���́~�̐��͂b���́��̐��Ɠ����R�ƂȂ�B
�a���́��̐��́i���|�R�j�~�R�|�R���R���|�P�Q�ƂȂ�B
��ӂ���A�`���́��̐��Ƃa���́��̐��͓����B
�`���́��̐����R���|�P�Q�ƂȂ�B
�\�̑S�̂́��̐��́A�i�a���́��̐��{�c���̊ۂ̐��j�~�Q
�Ȃ̂Łi�R���|�P�Q�{�R�j�~�Q���U���|�P�W�ƂȂ�B
����A���l�̃��[�O��̑ΐ퐔�́A
���~�i���|�P�j���Q�ŁA���̐������ΐ�\�Ɂ����t���̂ŁA
���~�i���|�P�j���Q���U���|�P�W
�ƂȂ�Ȃ���Ȃ�Ȃ��B
����������ƁA
���~���|�P�R���{�R�U���O
�i���|�S�j�i���|�X�j���O
�]���āA�����S�C�X
�����������S�̏ꍇ�͂a���́��̐����O�ƂȂ�A���ʂR�l������ʂP�l�̐��т��Ⴍ�Ȃ��Ă��܂��̂ő�ӂ����Ȃ��B
�]���āA�X�l�ȊO�͉��������B
�y���R�z
�ΐ�҂��l�A���ʂ��l�ōl����B�i���������P�j
�c���́��̐��͂��~�i���|�P�j���Q
�b���́��̐��͂��~�i���|�P�j���Q
�a���́��̐��͂��~�i���|���j�|���~�i���|�P�j���Q
�`���́��̐��͂��~�i���|���j�|���~�i���|�P�j���Q
�����̍��v�́A�Q���~�i���|���j
���l�̑ΐ퐔�Ɠ����Ȃ̂ŁA
���~�i���|�P�j���Q���Q���~�i���|���j
���~���|�i�S���{�P�j�~���{�S���~�����O
����������ƁA
�����o�S���{�P�}���[�g�i�W���{�P�j�p���Q
���͐����Ȃ̂ŁA�W���{�P�͊�̂Q��łȂ���Ȃ�Ȃ��B
�W���{�P���i�Q���{�P�j�~�i�Q���{�P�j
�i�Q���{�P���O�C���͐����j�ƒu���B
�����P�ɑ��A�����P�ƂȂ�B
�����������
�������~�i���{�P�j���Q�ƂȂ�B
���Ƃ��{�P�͂ǂ��炩���K�������ɂȂ�̂ŁA���͐����Ƃ������������B
�܂��A���̂Ƃ��������ŕ\���ƁA
�����o�Q���i���{�P�j�{�P�}�i�Q���{�P�j�p���Q
�����������
�����i���{�P�j�~�i���{�P�j�܂��͂��~��
�ł�������������ƂȂ�B
���ɁA���l�����ʂƊm�肷�邽�߂ɂ́A���ʂ��l�̏������i���̐��j�ω��������_�ȉ����グ�������A ��ʂ��|���l�̒N�̏����������������Ȃ���Ȃ�Ȃ��B
�S���A���ʂ��l�Ƃ̑ΐ�ŏ������̔����邱�Ƃ���A���ʂ��l�Ƃ̑ΐ�ł̏������̐��ōl���Ă������͓����B
���ʂ��l�̊Ԃł̑ΐ퐔�i�����̐��j�A�����c���́��̐��́A
���~�i���|�P�j���Q
���ʂ��l�̕��ς́@�i���|�P�j���Q�@�ƂȂ�B
����̏����_�ȉ����グ�����́A
������̂Ƃ��A�@�i���|�P�j���Q
���������̂Ƃ��A�@�����Q�ł���B
��ʂ��|���l���S�Ă��̐������Œ�P�����������Ȃ���Ȃ�Ȃ��̂ŁA�a���́��̐��́A�ȉ��̐����ȏ�łȂ���Ȃ�Ȃ��B
������̂Ƃ��A�@�i���|���j�~�o�i���|�P�j���Q�{�P�p
���������̂Ƃ��A�@�i���|���j�~�i�����Q�{�P�j
�a���́��̐��͂��~�i���|���j�|���~�i���|�P�j���Q�@�Ȃ̂ŁA�ȉ��̕s���������K�v������B
�i�P�j������̂Ƃ�
���~�i���|���j�|���~�i���|�P�j���Q���i���|���j�~�o�i���|�P�j���Q�{�P�p
�Q���~�i���|���j�|���~�i���|�P�j���i���|���j�~�i���{�P�j
�i���|���j�~�i���|�P�j�|���~�i���|�P�j���O
�i���|�P�j�~�i���|�Q���j���O
�����P�Ȃ̂ŁA�����P�܂��͂����Q��
�������Ȃ̂ŁA�����P�̂Ƃ������Q�ƂȂ肎���Q�������̂ŁA
�܂Ƃ߂ā@�����Q��
�����Q�~�o���~�i���{�P�j���Q�p
�������~���{��
����͂��~�������傫���A�i���{�P�j�~�i���{�P�j�����������B
�]���āA���͂����i���{�P�j�~�i���{�P�j�����ł���A
�܂����̉��͂����Q���̏��������B
�i�Q�j���������̂Ƃ�
���~�i���|���j�|���~�i���|�P�j���Q���i���|���j�~�i�����Q�{�P�j
�Q���~�i���|���j�|���~�i���|�P�j���i���|���j�~�i���{�Q�j
�i���|���j�~�i���|�Q�j�|���~�i���|�P�j���O
�i���|�Q�j�~���|���i�Q���|�R�j���O
�i���|�Q�j�~�������i�Q���|�R�j
�����ŁA�����Q�̂Ƃ��A�O���Q�@�ŏ��������Ȃ��B
�P�������Q�̋����͖����B
�����Q�̂Ƃ��A���ӂ����|�Q�Ŋ����āA
�������~�i�Q���|�R�j���i���|�Q�j
�������~�i���{�P�j���Q�������āA
�����i���~���{���j���Q�~�i���~���{���|�R�j���i���~���{���|�S�j�~�Q
�����i���~���{���j�~�o�P�{�P���i���~���{���|�S�j�p
�E�ӂ̑O���͂��~�������傫���A�㔼�͂P�����傫���̂ŁA
�������~���̉��͖����B
�����i���{�P�j�~�i���{�P�j�̉��ɂ��Ă͂��ꂾ���ł͂킩��Ȃ��B
�i���{�P�j�~�i���{�P�j�|�o�i���~���{���j�~�i���~���{���|�R�j���i���~���{���|�S�j�p���O
�����藧�Ă����i���{�P�j�~�i���{�P�j�͏����������ƂɂȂ�B
�i���{�P�j�~�i���{�P�j�~�i���~���{���|�S�j�|���~�i���{�P�j�~�i���~���{���|�R�j���O
�i���{�P�j�~�i���~���{���|�S�j�|���~�i���~���{���|�R�j���O
���~���~���{�Q���~���|�R���|�S�|���~���~���|���~���{�R�����O
���~���|�S���O
�i���{�Q�j�~�i���|�Q�j���O
�����Q
��������Ȃ��̂͂����P�̎������ł��邪�A
�����P�̎��͂����Q�~�R���Q���P�Ŋ�ł��邽�߁A
���������ł���ΕK�������Q�������ƂɂȂ�B
�]���āA������ł������ł��A�������~���̉��͖����A
�����i���{�P�j�~�i���{�P�j�̉��͏��������B
���ʂƂ��āA
�����P�C�Q�C�@�R�C�@�S�C�@�T�C�@�U�C�D�D�D�ɑ��A
�����P�C�R�C�@�U�C�P�O�C�P�T�C�Q�P�C�D�D�D
�����S�C�X�C�P�U�C�Q�T�C�R�U�C�S�X�C�D�D�D
�����܂�B
��L�ȊO�̉��͖����B
��
�y���z
����X�|�[�c�ł́C���l�̎Q���I��S���̑�����̃��[�O��ŏ��ʂ����߂Ă��܂��B
���������̃X�|�[�c�ɂ͈����������Ȃ��Ƃ��܂��B
����̑ΐ�ł́A�I��͑S�������[�O��̍ʼn��ʂ��炋�l�܂ł̑I��Ƃ̑ΐ�ŏ������̂��傤�ǔ����܂����B
�ɉ�������Ƃ��������ŁA���Ƃ��ɓ��Ă͂܂鐔���͈ȉ��̏��������B
���̐������i�����P�C�Q�C�R�C�D�D�D�j�ɑ��A
�������~�i���{�P�j���Q
�����i���{�P�j�~�i���{�P�j
���R�͂���ȊO�ɉ��͖������Ƃ͏ؖ��ł��܂������A���̑ΐ�\���K�����邱�Ƃ͏ؖ���
���@���킩��܂���ł����B
�c�O�B
�����m���@���q�̗Y�L�@����̉�
�_�����~���~������
�~�_�~������������
�~���_�~����������
���~���_�~�~�~����
�~�~�~���_�����~��
���~�~���~�_�����~
�~�~�~���~�~�_���~
�~�~�~�~���~�~�_��
�~�~�~�~�~�����~�_
���ʂR�l�ȊO����ʐw�ƒ�`����B
�P�l������̎����������Ƃ����B
�����ɎQ�������l�͑S�ċ����̏��������グ������A�e�l�̏������͂U�C�S�C�Q�C�O�̂����ꂩ�ł���B
���̃Q�[���ɂ͈����������Ȃ��̂ŁA
�S���̏������v���S���̕������v���P�l������̎������w�l�����Q
��ʁi���|�Q�j�l���S�ĂU���i���ʂR�l�ɂR���O�s�j�����ƍl����ƁA
�i�����|�����j�̍��v�́A(���|�Q)(�P�Q�|��)�ƂȂ�B
���ۂɂ͉��ʂR�l���m�ł́A�R���R�s�ƂȂ邩��A���ʂR�l�͑S���ŁA�U���������ƂɂȂ�B
�܂�A��ʐw�͉��ʂR�l�ɁA���v�R�s���Ă���B
��ʐw�́i�����|�����j�̍��v�́A
(���|�Q)(�P�Q�|��)�|�P�Q�ƂȂ�B
���ꂪ���ʎO�l�́i�����|�����j
�܂�(�R���|�P�Q)�Ɠ���������A
(���|�Q)(�P�Q�|��)�|�P�Q��(�R���|�P�Q)
������Ƃ��āA��2�|�P�P���{�Q�S���O
�����W�܂��͂����R
��������(�Q���l���|�P)���A�l������l���͂X�l�܂��͂S�l
�������A�Q���l�����S�l�ł���ƁA��ʐw����l�������Ȃ��̂ŁA��ʐw��l�͉��ʂR�l�ɁA���v�R�s�A�܂�S�s���Ă��邱�ƂɂȂ�B
����ł͂Q�����Ă��鉺�ʂR�l����ʂɂ͂Ȃ�Ȃ��̂ŁA�l������l���͂X�l�̂݁B
���ؖ��I��聁
�X�l�������肦�Ȃ��̂ɂ͂��ǂ낫�܂����B
�@�� ���ւ��ǂ�
�@�� ���T�̖����