問題2は桁数を一般化した形で今年の河合塾(Z会共催)東大即応OP模試に出ていたそうです。
ちょっと驚きです。
◆広島県 清川 育男 さんからの解答
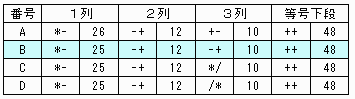
【問題1】
8*7-10=46
4*3-4=8
6+8-4=10
26+12+10=48
8*4-6=26
7-3+8=12
10+4-4=10
46-8+10=48
【問題2】
6 2 1 0 0 0 1 0 0 0
【問題1】の正解のすべてにチャレンジしてみました。
10+4-4=10
10-4+4=10
10*4/4=10
10/4*4=10
4通り
(8+7+10)+(4+3+4)+(6*8/4) (8+7+10)+(4-3+4)+(6+8+4) (8+7+10)+(4-3-4)-(6-8*4) (8+7+10)-(4+3-4)-(6-8*4) (8+7+10)-(4*3/4)-(6-8*4) (8+7-10)+(4-3+4)+(6+8*4) (8+7-10)*(4*3-4)+(6+8/4) (8+7-10)*(4*3*4)-(6*8*4) (8+7*10)+(4-3+4)*(6-8-4) (8+7*10)+(4-3-4)*(6+8-4) (8+7*10)+(4*3-4)-(6+8*4) (8+7*10)-(4+3-4)*(6+8-4) (8+7*10)-(4-3*4)-(6+8*4) (8+7*10)-(4*3*4)+(6+8+4) (8+7*10)-(4*3/4)*(6+8-4) (8-7+10)+(4+3+4)-(6-8*4) (8-7-10)+(4+3/4)*(6*8/4) (8-7-10)+(4-3+4)+(6*8+4) (8-7-10)*(4+3*4)+(6*8*4) (8-7-10)*(4*3+4)+(6*8*4) (8-7-10)*(4/3-4)*(6-8+4) (8-7*10)+(4+3+4)*(6+8-4) (8*7+10)+(4+3-4)*(6-8-4) (8*7+10)+(4-3*4)-(6+8-4) (8*7+10)+(4*3-4)+(6-8*4) (8*7+10)+(4*3/4)*(6-8-4) (8*7+10)-(4+3*4)-(6-8+4) (8*7+10)-(4-3-4)*(6-8-4) (8*7+10)-(4-3*4)+(6-8*4) (8*7+10)-(4*3+4)-(6-8+4) (8*7+10)-(4*3-4)-(6+8-4) (8*7+10)*(4/3/4)-(6-8*4) (8*7+10)/(4+3+4)*(6+8/4) (8*7+10)/(4+3-4)-(6-8*4) (8*7+10)/(4*3/4)-(6-8*4) (8*7-10)+(4+3*4)/(6+8/4) (8*7-10)+(4-3+4)-(6/8*4) (8*7-10)+(4-3*4)+(6+8-4) (8*7-10)+(4*3+4)/(6+8/4) (8*7-10)+(4*3-4)+(6-8-4) (8*7-10)+(4*3-4)/(6-8/4) (8*7-10)-(4+3*4)+(6+8+4) (8*7-10)-(4-3*4)+(6-8-4) (8*7-10)-(4-3*4)/(6-8/4) (8*7-10)-(4*3+4)+(6+8+4) (8*7-10)-(4*3-4)+(6+8-4) (8*7-10)-(4/3/4)*(6-8-4) (8*7*10)+(4/3-4)*(6*8*4)48通り
4*48=192通り。
◆愛知県 Y.M.Ojisan さんからの解答
【問題1】
8+7+10=25
4-3+4=5
6+8+4=18
26+12+10=48
8*4-6=26
7-3+8=12
10-4+4=10
25+5+18=48
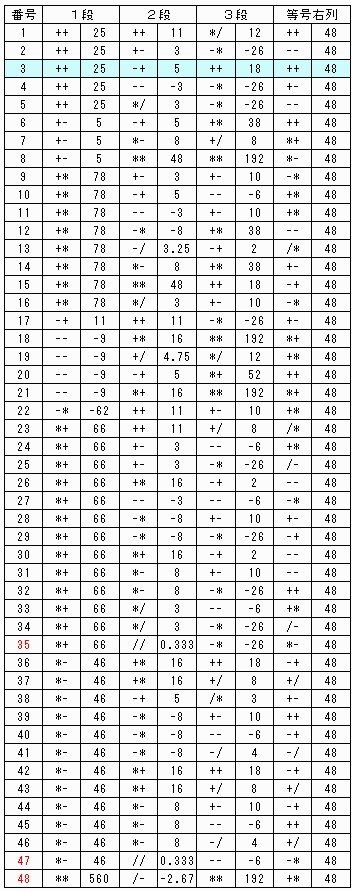
PCで調べると結構たくさんあり、48×4とおりでした。
解答はB-3の組み合わせです。
段の35,47,48番は小数点以下の問題で確認できませんでした。

【問題2】
6210001000
◆埼玉県の高校生 解凍紳士 さんからの解答
【問題1】
8*7+10=66
4*3+4=16
6-8+4=2
26+12+10=48
8*4-6=26
7-3+8=12
10+4-4=10
66-16-2=48
[解法]
まずは一番下の横段と、一番右の列以外の縦列の計算はすぐにできる。
残りは横段の計算だが、自分の場合は最初に最上段の計算を固定して、その後他の横段の値を強引にはじき出す方法で計算した。
まぁ気合で計算できる問題だから[解法]と呼べるほど格好いいものは書けないが…(^^;
【問題2】
[答]6210001000
[解法]
この手の問題は一番厄介なものから処理していくと案外簡単に求まるものだ。
具体的には大きい値から処理をしてゆくとよい。と、言うわけで10桁目から計算する。
仮に10桁目の数が1であった場合他の桁に「9」を割り当てなければならない。
すると今度はその桁を仮に1桁目だとすると「0」が9箇所に当てはめられなければならないので、10桁に収まりきらない。
(「2」以上の数は論外。)
故に10桁目は「0」である。
同様の理由で9桁目も「0」。
次に8桁目が「1」であった場合、「0」を七箇所に入れると、残り一箇所の値に何を入れても問題の条件に合致しない。
故に8桁目も「0」
では7桁目に「1」を入れた場合はどうか?
これは桁数が大きいほうから「0」を代入していくと2桁目と3桁目が残ることになる。
ここで2桁目は「1」なので7桁目に「1」が一箇所あり、ここに「1」は入り得ないので「2」を入れてみる。
すると「2」が一つ発生するので3桁目に「1」を代入する。
すると今度は先刻2桁目に代入した「「1」の個数は2個」という事柄に一致する。
よって全ての条件を満たす値は「6210001000」である。
◆千葉県 なのはな子 さんからの解答
【問題1】
8+7+10=25 4+3+4=11 6*8/4=12 26+12+10=48 8*4-6=26 7-3+8=12 10-4+4=10 25+11+12=48---以下、同じ部分は省略---
8+7+10=25 4-3+4=5 6+8+4=18 25+5+18=48 -------------- 8+7-10=5 4-3+4=5 6+8*4=38 5+5+38=48 -------------- 8+7-10=5 4*3-4=8 6+8/4=8 5*8+8=48 -------------- 8+7-10=5 4*3*4=48 6*8*4=192 5*48-192=48 -------------- 8*7-10=46 4*3-4=8 6+8-4=10 46-8+10=48 -------------- 8*7-10=46 4*3+4=16 6+8/4=8 46+16/8=48 -------------- 8*7-10=46 4*3+4=16 6+8+4=18 46-16+18=48 -------------- 8*7+10=66 4*3-4=8 6+8-4=10 66-8-10=48 -------------- 8+7*10=78 4*3*4=48 6+8+4=18 78-48+18=48 -------------- 8+7*10=78 4*3-4=8 6+8*4=38 78+8-38=48 -------------- 8+7*10=78 4+3-4=3 6+8-4=10 78-3*10=48 --------------◆解く順序
(26,12,10)→縦の各列(8,4,6)、(7,3,8)、(10,4,4)→横の各列(8,7,10)、(4,3,4)、(10,4,4)の計算が「48」になる記号
(26,12,10)は、2箇所とも「+」で、26+12+10=48となり正しい。
(8,4,6)は、2箇所とも「+」では26には不足なので「X」である。
8X4=32なので、もう1個所は「−」である。
8X4-6=26
(7,3,8)は、2箇所とも「+」では12より多い。
どちらかを「X」にすると、奇数と偶数の組み合わせになり、合計で「12」にはなり得ない。
「÷」では割り切れない。
「−」にすると(7−3)で、もう1個所は「+」である。
7-3+8=12
(10,4,4)は、「10」にするには、4を「+」と「−」(または「X」と「÷」)で0にする。
10+4-4=10(10-4+4=10)、10X4÷4=10
--------------
(8,7,10)・・・
8+7+10=25、8+7−10=5、8−7+10=11、8X7-10=46、
8X7+10=66、8+7X10=78、8X7X10=560
(4,3,4) ・・・
4+3+4=11、4+3−4=3(4X3÷4=3)、4−3+4=5、4X3−4=8、
4X3X4=48、4X3+4=16(4+3X4=16)、
(6,8,4) ・・・
6+8+4=18、6+8−4=10、6+8X4=38、6+8÷4=8、
6X8−4=44、6X8+4=52、6X8÷4=12、6X8X4=192
*いろいろな記号で計算した数から、合計で「48」になる組み合わせは、次の通り。
25+11+12=48、25+5+18=48、 5+5+38=48、 5x8+8=48、
5x48-192=48、 46+16÷8=48、46-8+10=48、 46-16+18=48、
66-8-10=48、 78-48+18=48、78+8-38=48、 78-3x10=48
【問題2】
6210001000
1桁目の数をnとすると、(n+1)桁目は少なくとも「1」である。
すると2桁目は、1ということはあり得ないので、少なくとも「2」である。
2桁目が「2」であるとすると、3桁目は「1」である。
10桁のうち、残りは6桁である。
残り6桁を「0」とすると、1桁目は「6」である。
したがって条件に合う10桁の数は、 6210001000 である。
◆大阪府 ゆたか さんからの解答
【問題1】
8+7+10=25
4-3+4=5
6+8+4=18
26+12+10=48
8*4-6=26
7-3+8=12
10-4+4=10
25+5+18=48
【問題2】
各位の数字を大きい方から順にA(0),A(1),A(2),・・・,A(9)とします。
すなわち、この10個の数字の中にnがA(n)個含まれることになります。
数字は全部で10個ですから、
A(0)+A(1)+A(2)+・・・+A(9)=10 ・・・(1)
つまり各位の数字の合計は10ですから、
0*A(0)+1*A(1)+2*A(2)+・・・+9*A(9)=10 ・・・(2)
今、「5」以上の数字が2個以上あると、結果として各位の数字の合計は10を超えてしまいます。
また、「5」以上の数字が1つもないとすると、
A(5)=A(6)=A(7)=A(8)=A(9)=0となり、
「0」が5個以上あることになるので矛盾が生じます。
よって、A(5)+A(6)+A(7)+A(8)+A(9)=1
そして、A(0)+A(1)+A(2)+A(3)+A(4)=9
さて、A(5),A(6),A(7),A(8),A(9)の中に「0」が4個、「1」が1個あるので、
特に、A(0)≧4、A(1)≧1です。
ところが、A(1)=1とすると、「1」が2個以上になるのでこれも矛盾です。
また、A(1)≧3とすると、「2」以上の3つの数字が1個ずつあり、それらの和は9を超えるため、(2)が成り立ちません。
よって、A(1)=2であり、題意と(2)よりA(2)=1です。
あとは容易にA(3)=A(4)=0,A(0)=6がわかりますから、
求める数は「6210001000」です。
◆ 問題へもどる
◆ 今週の問題へ