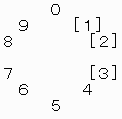
◆愛知県 Y.M.Ojisan さんからの解答
【問題1】
左+→0,中+→1,右+→3
左−→4,中−→0,右−→0
により 1 1 1 にできる。
【問題2】
現在の目を a,b,c 加算値 を A,B,C ぞろ目値を Z とすると
A+B+C=0
(a+A)+(b+B)+(c+C) ≡3*Z (mod 10 以降省略)
でなければならないから a+b+c≡3*Z でなければならない。
3と10は互いに素であるから 任意のa+b+cに対してZは存在する。
すなわち 3-1≡7 であるから Z≡(a+b+c)*7 である。
ちなみに 問題1の場合 (a+b+c)*7=13*7≡1
【おまけ】
10=2*5 であるから10は5以外の奇素数と互いに素である。
従って、5の倍数でない奇数は10を法として逆数が必ず存在する。
以下問題2と同じであり具体的には、
目の合計値×P(n) mod 10 により目標とする目の値を計算する。
ここでP(n)は桁数nの下1桁で決まる値で
P(1)=1 P(3)=7 P(7)=3 P(9)=9 である。
【P.S.】
奇数桁数でも15桁の場合は5を含んでおり、10を法として逆数は存在しない。
したがって、目の合計が5の倍数でないと必敗である。
一方、目の合計が5の倍数の場合は必勝であって、目標とする目は、目の合計が5の偶数倍の場合は0、奇数倍の場合は1である。
これは、P(5)=1/5 と形式的に書ける。
◆千葉県 なのはな子 さんからの解答
【問題1】
1,1,1 のゾロ目にする。
左+→0,中+→1,右+→3
左−→4,中−→0,右−→0
または、
左+→6,中+→1,右+→0
左−→0,中−→0,右−→7
【問題2】
勝ちにできるゾロ目の計算法
◆ 各桁の数字の和を桁数で割る。
例えば、1,2,3 と並んだ場合、
1+1(または、−9)、3−1(または、+9) で「+」「−」の回数が等しく、2,2,2 のゾロ目となる。
[1+2+3=6 6÷3=2 なので、 数字の和を桁数で割ると、勝ちにできるゾロ目がわかる。]
◆「−ボタン」か「+ボタン」かを決める方法
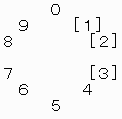
右回りは、「+ボタン」の回数・・・「1」から右回りなら1回で「2」
左回りは、「−ボタン」の回数・・・「1」から左回りなら9回で「2」
◆「問題1」の場合、5+0+8=13 となり、3では割り切れない。
それぞれの数は、0から9までの10個の数の中を遷移するだけなので、±10をしても同じ結果になる。
だから、「問題1」場合は10を引いて、3÷3=1となり、「1」が勝ちにできるゾロ目になる。
また、2,4,5 と並んだ場合、2+4+5=11 となり、3では割り切れない。
10を足すと、21÷3=7となり、「7」のゾロ目となる。
【おまけ】
「5」以外は、1から9までのどの数も、問題1と同じ方法で割り切れるが、「5」は0と5の場合しか割ることができない。
◆富山県 萩の葉 さんからの解答
【問題2】
3数をA1,A2,A3と置き、それぞれa1,a2,a3だけ移動するものとする。
移動する数については
a1>0 a2>0 a3<0
a1>0 a2=0 a3<0
a1>0 a2<0 a3<0
の3通りがある。移動し終えたゾロ目Pは
A2+a2+10 A3+a3+10
A1+a1 A2+a2 A3+a3
A1+a1-10 A2+a2-10
の8パターンが考えられ3Pは
(A1+A2+A3)+(a1+a2+a3)+20
(A1+A2+A3)+(a1+a2+a3)+10
(A1+A2+A3)+(a1+a2+a3)
(A1+A2+A3)+(a1+a2+a3)-10
(A1+A2+A3)+(a1+a2+a3)-20
のいずれかになる。a1+a2+a3=0なので3Pは
(A1+A2+A3)+20 =(A1+A2+A3)+2+(3×6)
(A1+A2+A3)+10 =(A1+A2+A3)+1+(3×3)
(A1+A2+A3) =(A1+A2+A3)
(A1+A2+A3)-10 =(A1+A2+A3)-1-(3×3)
(A1+A2+A3)-20 =(A1+A2+A3)-2-(3×6)
となり
(A1+A2+A3)+2
(A1+A2+A3)+1
(A1+A2+A3)
(A1+A2+A3)-1
(A1+A2+A3)-2
の内、少なくともひとつは3の倍数になる。
よってゾロ目Pは3数の和を3で割った数。
割り切れなければ3数の和±10または±20を3で割れば求めることができる。
【おまけ】
同様にしてn個の数A1,A2,A3・・・Anのゾロ目はn個の数の和をnで割った数。
割り切れなければn数の和±10または±20,・・・±10(n-1)をnで割れば求めることができる。
ただしnが偶数の場合はn数の和が奇数の時、±10,±20,±30と偶数をいくら加えても偶数nで割ることはできないので適用できない。
また、nが5の倍数の場合はn数の和が5の倍数でない時、±10,±20と10の倍数をいくら加えても5の倍数にならないのでnで割ることはできず適用できない。
◆東京都 明 さんからの解答
【問題1】
左+→0,中+→1,右+→3
左−→4,中−→0,右−→0
【問題2】
ゲーム機の各桁のボタンをいくつか押して、同じ数字を並べたとして、ここから、ボタンを押す数を変えた時、数字がどのように変わるか を考えます。
【問題1】では「+」ボタンのみを押して0.0.0とするためには
左+→5,中+→0,右+→2 であり、
「+」を押した数と「-」を押した数の差は +7 となります。
(このゲーム機で実際やると「あなたの負けです」が出ますが、[OK」をクリックすると続けてゲームを進めることができました。)
ここから1つの桁、例えば左の桁の「-」ボタンを10回押して逆転させると桁の数字は元にもどりますが、押した回数は
左+→5,中+→0,右+→2
左−→10,中−→0,右−→0 となり、
「+」「-」を押した数の差は-3 となります。
(始めからスタートした場合、この状態は左のボタンを +5-10=-5 とした
左+→0,中+→0,右+→2
左−→5,中−→0,右−→0 と同じです。)
ここから各桁の「+」ボタンを1回ずつ押すと、数字は1.1.1となり、
左+→6,中+→1,右+→3
左−→10,中−→0,右−→0 となり、
「+」「-」を押した数の差は 0 となって、めでたく「あなたの勝ちです」が出ます。
各桁ごとに「+」「-」のボタンを押した数の差を求めると【問題1】の答えとなります。
(上の操作で逆転させる桁を変えても並ぶ数字は1.1.1となります。)
一般化して、初期に並んだ数字を各桁の「+」ボタンのみを押して0.0.0にするために押した回数の総計をcとすると、逆転させる桁の数をx、「+」「-」ボタンを押した数の総計が一致した時に並んだ数がyとして、
10(-x)+ 3y= -c ・・・(1) が成り立つ。
10(-x)+ 3y= -1 の解は目算で、x=1 y=3
したがって(1)の解はx=c y=3c となる。
yは10ごとに一回転して元に戻るので10で割った余り、
3c(mod10)が答えとなる。
【おまけ】
整数pとqが互いに素(最大公約数が1)の場合、
px + qy= 1 となる整数 x,y が存在することが保証されているので
p=10とすると、q が5の倍数以外の奇数(10と互いに素)の場合【問題2】と同じ方法でx,yを求めることができる。
(qが5の倍数、もしくは偶数の場合、px+qy は5または2の約数を持つので
px+qy≠1は明らか。)
10(-x)+3y=-1 の解は x=1 y=3 (【問題2】)
10(-x)+7y=-1 の解は x=5 y=7
10(-x)+9y=-1 の解は x=1 y=1
10(-x)+1y=-1 の解は x=1 y=9
10 (-x)+(10a+3)y=-1 (aは0以上の整数)の解は
10(-x+ay)+3y=-1 から x-ay=1 y=3
以上から、初期に並んだ数字を各桁の「+」ボタンのみを押して0.0.0にするために押した回数の総計をcとすると、一致する数yは
桁数が10a+1 のとき y=9c(mod10)
桁数が10a+3 のとき y=3c(mod10)
桁数が10a+7 のとき y=7c(mod10)
桁数が10a+9 のとき y=c (mod10)
◆東京都 藤本 さんからの解答
【問題1】
左+→0,中+→1,右+→3
左−→4,中−→0,右−→0
【問題2】
ゲーム機に与える数をi、j、k とする。
ここでp = i+j+kとすると、
p、p+10、p+20のいずれかは、3で割り切れる
(∵ 3 と10 が互いに素 )
この 3で割り切れる数をqとすると
q/3 (mod 10)が 求めるゾロ目の数になります。
【おまけ】
n桁の数を
(a1,a2,…,an) 0≦ni≦9 (i=1,2,…,n)
とする
+ボタンとーボタンを同じ回数押してゾロ目にするということは
a1〜an の平均にあわせることになる
ここで 0を超えてボタンを押していくということは
もとの aiを ai+10 として平均を計算することを意味します
つまり ゲームに勝つゾロ目の数の求め方は
Σai、Σai + 10、Σai + 20、…、Σai + (n-1)*10
のうち nで割り切れるものをみつける
(仮定より n と 10 は互いに素 なので必ず見つかる)
これを m とし、m/n(mod10)を求めることで得られる。
◆ 問題へもどる
◆ 今週の問題へ