◆大阪府の高校生 Alpha Omega さんからの解答
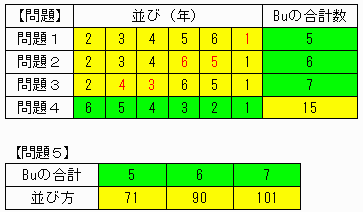
【問題1】
6,1,2,3,4,5
【問題2】
6,1,2,3,5,4
【問題3】
6,1,3,2,5,4
【問題4】
6,5,4,3,2,1のときが最大で、15回。
【問題5】【おまけ】
全員学年が異なるn人について、文句の数の合計がa回になるような並び方を
f(n,a) (通り) とする。(0≦a≦n(n-1)/2)
そして以下のようにして漸化式を作る。
まず、n-1人を並ばせる。
次にn人目(今並んでいるn-1人より学年は上)を並ばせるときにそのn人が文句をa回言うようにn人目を配置する。
つまり、n-1人が a-k (0≦k≦a) (回) 文句を言うとき、
n人目を先頭からa-k(番目)と a-k+1(番目) の間に配置すればよい。
(k=0のときは先頭に、k=aのときは最後尾に配置する)
またこのように配置する方法は f(n-1,a-k) (通り)である。
すべてのkについて、その値によって決まる配置の方法は互いに排反である。
したがって、
n-1≧a のとき
f(n,a) = f(n-1,a) + f(n-1,a-1) + f(n-1,a-2) +...+ f(n-1,1) + f(n-1,0)
n-1<aのとき
f(n,a) = f(n-1,a) + f(n-1,a-1) + f(n-1,a-2) +...+ f(n-1,-n+a+2) + f(n-1,-n+a+1)
であるが、m<0 または m>n(n-1)/2 のとき f(n,m)=0 と定めれば、どんなaに対しても
f(n,a) = f(n-1,a) + f(n-1,a-1) + f(n-1,a-2) +...+ f(n-1,-n+a+2) + f(n-1,-n+a+1) ...(1)
と表せる。
さらに、
f(n,a-1) = f(n-1,a-1) + f(n-1,a-2) +...+ f(n-1,-n+a+1) + f(n-1,-n+a) ...(2)
(1)-(2)をすれば
f(n,a) - f(n,a-1) = f(n-1,a) - f(n-1,-n+a)
となる。
また、漸化式の初期条件としては、n人が一度も文句を言わない場合、
すなわち、1,2,3,4,...,n の順に並んだ場合を採用する。
(つまり、f(n,0)=1)
まとめると、
f(n,a)= 0 (a<0 または n(n-1)/2<a)
f(n,a)= 1 (a=0)
f(n,a)=f(n,a-1) + f(n-1,a) - f(n-1,-n+a) (0<a≦n(n-1)/2)
この式を使えばどんなn,aについても求めることができます。
(問題5の答え)
私は、計算に自信がないのでコンピュータにやらせました。
以下のコードはVisual basic で記述しました。
///////////////////////////
Function f(n As Long, a As Long)
'f(n,a)を求める為の関数
If a = 0 Then
f = 1
ElseIf a < 0 Or n * (n - 1) / 2 < a Then
f = 0
Else
f = f(n, a - 1) + f(n - 1, a) - f(n - 1, a - n)
End If
End Function
///////////////////////////
結果:
f(6,5)=71
f(6,6)=90
f(6,7)=101
◆東京都 藤本 さんからの解答
【問題1】
2,3,4,5,6,1
【問題2】
3,2,4,5,6,1
【問題3】
3,4,2,5,6,1
【問題4】
15回
並び方 6,5,4,3,2,1
【問題5】
5回 71通り
6回 90通り
7回 101通り
生徒が2人の場合(5,6年生だけの場合)
文句の回数
0回 1通り
1回 1通り
2回以上 0通り
ここに 4年生が加わって3人になった場合
・4年生が文句をいう回数は
先頭の場合 0回
2番目の場合 1回
3番目の場合 2回
の3通り
・5,6年生が文句をいう回数は 2人だけの場合と同じ
このことから 3人の場合の文句の回数は
文句の回数 0回 2人の場合の 0回 =1回 1回 2人の場合の 0〜1回の合計 =2回 2回 2人の場合の 0〜2回の合計 =2回 3回 2人の場合の 1〜3回の合計 =1回 N(≧4)回 2人の場合の N−2〜N回の合計=0回同じように さらに3年生が加わって4人になった場合
文句の回数 0回 3人の場合の 0回 =1回 1回 3人の場合の 0〜1回の合計 =3回 2回 3人の場合の 0〜2回の合計 =5回 3回 3人の場合の 0〜3回の合計 =6回 4回 3人の場合の 1〜4回の合計 =5回 5回 3人の場合の 2〜5回の合計 =3回 6回 3人の場合の 3〜6回の合計 =1回 N(≧7)回 3人の場合の N−3〜N回の合計=0回これを順次繰り返して
文句の回数 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 ------------------------------------------------------------------------------- 2人 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3人 1 2 2 1 0 0 0 0 0 0 0 0 0 0 0 0 4人 1 3 5 6 5 3 1 0 0 0 0 0 0 0 0 0 5人 1 4 9 15 20 22 20 15 9 4 1 0 0 0 0 0 6人 1 5 14 29 49 71 90 101 101 71 49 29 14 9 5 1
【おまけ】
どこまで問題を一般化するのかよくわかりませんが。。。。
6年生は どこに並んでも 文句はいわない
5年生は 6年生より前ならば 文句をいわない
後ならば 1回文句をいう
4年生は 4〜6年生の中で
1番前ならば 文句を言わない
2番目ならば 文句を1回いう
3番目ならば 文句を2回いう
3年生は 3〜6年生の中で
1番前ならば 文句を言わない
2番目ならば 文句を1回いう
3番目ならば 文句を2回いう
4番目ならば 文句を3回いう
……
と 上級生から順に文句をいう回数を求めて加算する
◆千葉県 トリガラJr さんからの解答
学年だけ並べると
【問題1】
6,1,2,3,4,5
【問題2】
6,2,1,3,4,5
【問題3】
6,2,3,1,4,5
【問題4】
6,5,4,3,2,1に並んだときの15個
【問題5】
1年生からn年生までの時の並び方を考える.
そのときBuがm回になる並び方をSnm,
その並び方の個数をBnmで表す.
S20は1,2 よってB20=1
S21は2,1 よってB21=1
S20がa1,a2
S21がb1,b2 とする.
3年生をそこに加えることを考える.
3年生が入るとそれより後ろの人はみなBuと1回ずついうことより
S30はa1,a2,3
よってB30=B20=1
S31はa1,3,a2またはb1,b2,3
よってB31=B20+B21=2
S32は3,a1,a2またはb1,3,b2
よってB32=B20+B21=2
S33は3,b1,b2
よってB33=B21=1
S30=a1,a2,a3
S31=b1,b2,b3
S32=c1,c2,c3
S33=d1,d2,d3 とする.
4年生をそこに加えることを考える.
S40はa1,a2,a3,4
よってB40=S30=1
S41はa1,a2,4,a3またはb1,b2,b3,4
よってB41=S30+S31=3
S42はa1,4,a2,a3またはb1,b2,4,b3 またはc1,c2,c3,4
よってB42=B30+B31+B32=5
S43は4,a1,a2,a3またはb1,4,b2,b3またはc1,c2,4,c3またはd1,d2,d3,4
よってB43=B30+B31+B32+B33=6
S44は4,B1,B2,B3またはc1,4,c2,c3またはd1,d2,4,d3
よってB44=B31+B32+B33=5
S45は4,c1,c2,c3またはd1,4,d2,d3
よってB45=B32+B33=3
S46h4,d1,d2,d3
よってB46=B33=1
同様にして
B50=B40=1 B51=B40+B41=4 B52=B40+B41+B42=9 B53=B40+B41+B42+B43=15 B54=B40+B41+B42+B43+B44=20 B55=B41+B42+B43+B44+B45=22 B56=B42+B43+B44+B45+B46=20 B57=B43+B44+B45+B46=15 B58=B44+B45+B46=9 B59=B45+B46=4 B510=B46=1 B60=B50=1 B61=B50+B51=5 B62=B50+B51+B52=14 B63=B50+B51+B52+B53=29 B64=B50+B51+B52+B53+B54=49 B65=B50+B51+B52+B53+B54+B55=71 B66=B51+B52+B53+B54+B55+B56=90 B67=B52+B53+B54+B55+B56+B57=101 B68=B53+B54+B55+B56+B57+B58=101 B69=B54+B55+B56+B57+B58+B59=90 B610=B55+B56+B57+B58+B59+B510=71 B611=B56+B57+B58+B59+B510=49 B612=B57+B58+B59+B510=29 B613=B58+B59+B510=14 B614=B59+B510=5 B615=B510=1よって5回 71通り,
【おまけ】
n番目にm年生がいる状態をn-mで表し,これをnの小さい順に並べる
-でつながれた2数が一致していない一番左の組をa-bとする.
ここで、この組の右の数bを順序からも学年からも省いて再び並べ直し-でつながれた2数が一致していない一番左の組に対し同じ操作をする
これを、−でつながれた2数がすべて一致するまで繰り返す.
-でつながれた2数が一致していなかったすべての組a-bに対し,b-○が左からc番目にあるときc−aをすべて加えたものが求めるBuの数.
例
1番目1年生,2番目4年生,3番目3年生,4番目2年生,5番目5年生,6番目6年生を
1-1,2-4,3-3,4-2,5-5,6-6 と表す.
-でつながれた2数が一致していない一番左の組は2-4・・・a
この組の右の数4を左側に持つ組は左から4番目の4-2.
この4番目の「4」とaの左の数「2」の差は2・・・(1)
ここで、この組の右の数4を順序からも学年からも省いて再び並べ直すと
1番目1年生,2番目3年生,3番目2年生,5番目5年生,6番目6年生
1-1,2-3,3-2,5-5,6-6
-でつながれた2数が一致していない一番左の組は2-3・・・b
この組の右の数3を左側に持つ組は左から3番目の3-2.
この3番目の「3」とbの左の数「2」の差は1・・・(2)
ここで、この組の右の数3を順序からも学年からも省いて再び並べ直すと
1番目1年生,2番目2年生,5番目5年生,6番目6年生
1-1,2-2,5-5,6-6
-でつながれた2数はすべてが一致.ここで操作終了.
(1)(2)を足し3がBuの数.
◆愛知県 Y.M.Ojisan さんからの解答

∵ 一般にn種類年の場合を考える。
これを先頭の1人と後続のn-1種類年のグループに分けると、
先頭の人がm番目(=1〜n)年生のとき後続のグループは合計m−1回Buと言い、
これにn-1種類年のグループのBuの言い方が加算される。
n=2 のとき 並び方は全部で2!とうりであり、このうちBu0回が1とおり、Bu1回が1とおりである。
n=3の時は 先頭が1年生なら 後続のグループは1年生に対してBuと言わないのでn=2のBuの状態と同じ。
2年生なら後続のグループは1回BuというのでBu1回が1とおりでBu2回が1とおり。。。。。
以上を繰り返すと下表のように計算できる。
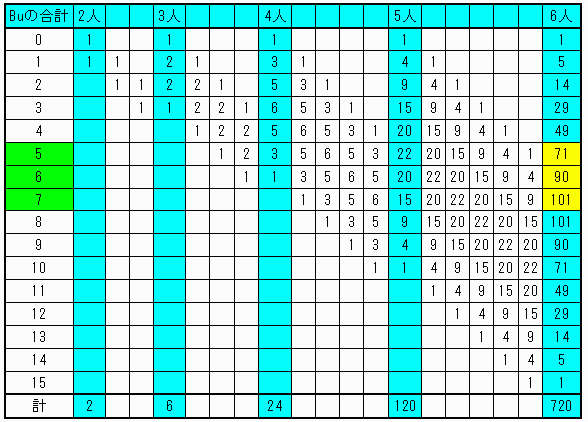
【おまけ】
文句が0回である1年から6年まで順に並んでいる状態を「定位置」とよぶことにする。
最も単純かつ確実に数える方法の一つは、上級生から順に定位置に下がって行き、すれ違いのときに文句を何回言われたかを積算する方法である。
数え方の良い方法の評価を、上級生順次探索+すれ違いの数の平均が小さい方法としたとき、この方法は18.55です。
もう少し改良を考えます。
(1) 前の人から順次定位置に下がりますが、文句をいわれたときだけ下がり、言われなくなったら、下がるのをその上級生にバトンタッチします。
未定の最上級生が定位置に着いたら、また前の人から繰り返します。
この場合、上級生順次探索の手順が一部省かれるので、評価値は15です。
(注 並びによらず全部15である)
(2) ほぼ同じ手順ですが、たとえば6年生が下がってゆく途中で、1年下の5年生(が最上級であるグループ)にであったら、合計メンバ2人の1グループになり5年生として下がってゆきます。
さらに1年下の4年生(が最上級であるグループ)にであったら合計メンバ3人の1グループになり4年生として定位置まで下がってゆきます。
文句の数はすれ違うグループの人数の積を加算することになります。
なお、文句を言う側はグループの最上級生だけが言うとします。
この場合の評価値はグループ間でまとめて文句をいう効果により低減し、9.1です。
◆東京都 明 さんからの解答
【問題1】
隣あった生徒の入れ替えは、それ以外の生徒の「Bu」には影響せず、単に入れ替えた生徒の「Bu」を1つ増やすか、減らすかのいずれか。
したがって、隣あった生徒の入れ替えを一つづつ行って所要の回数にすればよい。
6.1.2.3.4.5. (5回)
【問題2】
6.1.2.3.5.4. (6回)
【問題3】
6.1.2.5.3.4. (7回)
【問題4】
全く逆に並んだ6.5.4.3.2.1.が最大で15回
【問題5】
生徒が1,2年生のみのとき並び方の数は
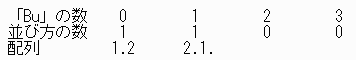
次に3年生を最後尾に入れ、前方の隣あった生徒と順に入れ替える操作をすると、
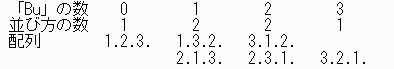
n年生まで並べた時の「Bu」の数pの並び方の数をN(n)pとすると、
N(n)p = N(n-1)p-n+1 + N(n-1)p-n+2 + ・・+ N(n-1)p
(ただしp-n+k が負のときは N(n-1)p-n+k = 0 )
であることから、順に4年生、5年生、6年生と加えていくことにより、順次並び方の数が求まる。
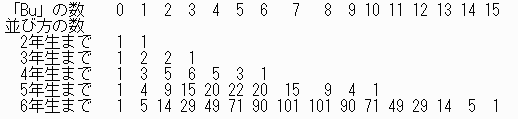
以上により、
5回 71 通り
6回 90 通り
7回 101 通り
【おまけ】
k番目の生徒の年次をMkとすると「Bu」の数 Bは
B = Σ(j<k) (1+(Mj-Mk)/|Mj-Mk|)/2
で求めることができますが、この式は定義を単に数式に翻訳しただけで、余り面白くありません。
◆広島県 清川 育男 さんからの解答
【問題4】
全結果はこちらです。
【おまけ】
小さい順に並べ替えるのに要する最小の置換回数
または
X1 X2 X3 X4 X5 X6
1 2 3 4 5 6
上段と下段と同じ数同士を線で結びそのとき出来る交点の数。
数列サイトで検索して見ました。
ID Number: A008302
Sequence: 1,1,1,1,2,2,1,1,3,5,6,5,3,1,1,4,9,15,20,22,20,15,9,4,1,1,5,
14,29,49,71,90,101,101,90,71,49,29,14,5,1,1,6,20,49,98,169,
259,359,455,531,573,573,531,455,359,259,169,98,49,20,6,1
Name: Triangle of Mahonian numbers T(n,k): coefficients in expansion of
Product (1+x+...+x^k); k=0..n.
Comments: T(n,k) = number of permutations of {1..n} with k inversions.
n-th row gives growth series for symmetric group S_n with respect to
transpositions (1,2), (2,3), ..., (n-1,n).
References L. Comtet, Advanced Combinatorics, Reidel, 1974, p. 240.
F. N. David, M. G. Kendall and D. E. Barton, Symmetric Function and
Allied Tables, Cambridge, 1966, p. 241.
D. Foata, Distributions eule'riennes et mahoniennes sur le group des
permutations, pp. 27-49 of M. Aigner, editor, Higher Combinatorics,
Reidel, Dordrecht, Holland, 1977.
P. de la Harpe, Topics in Geometric Group Theory, Univ. Chicago Press,
2000, p. 163, top display.
R. H. Moritz and R. C. Williams, A coin-tossing problem and some related
combinatorics, Math. Mag., 61 (1988), 24-29.
E. Netto, Lehrbuch der Combinatorik. 2nd ed., Teubner, Leipzig, 1927,
p. 96.
Links: B. H. Margolius, Permutations with inversions, J. Integ. Seqs. Vol. 4 (2001), #01.2.4.
Formula: Comtet and Moritz-Williams give recurrences.
G.f.: Product_{j=1..n} (1-x^j)/(1-x) = Sum_{k=1..M} C_{n,k} x^k,
where M = n(n-1)/2.
Example: 1; 1+x; (1+x)(1+x+x2) = 1+2x+2x2+x3; etc.
Maple: g:=proc(n,k) option remember; if k=0 then return(1) else if (n=1 and
k=1) then return(0) else if (k<0 or k>binomial(n,2)) then
return(0) else g(n-1,k)+g(n,k-1)-g(n-1,k-n) end if end if end if end
proc;
◆広島県 うとんた さんからの解答
一般に隣り合う人を入れ替えた場合、文句の総数の変化は±1である。
・前よりも後ろの学年が大きい、隣り合う2人組を入れ替えれば+1 …(1)
・後ろよりも前の学年が大きい、隣り合う2人組を入れ替えれば−1 …(2)
よって(1)をk回繰り返せば文句の数はkとなる。
ただし、0≦k≦n(n-1)÷2
(人数をnとした場合)
※問題1〜4に関しては、おまけが出来れば出来るので割愛します
【おまけ】
学年ごとの文句の回数を考えると、
・6年生:0
・5年生:0,1
・4年生:0,1,2
・3年生:0,1,2,3
・2年生:0,1,2,3,4
・1年生:0,1,2,3,4,5
となる。
文句の総数とは、それぞれの学年の文句の回数の和であることからその組み合わせを考えればよい。
※数え上げの際の補足説明
1、Cはコンビネーション。
2、()内は、学年ごとの文句の回数。
0は残りの組み合わせとなる(…×1)ので割愛。
●[文句の総数]:[組み合わせの数]
●0回:1通り
●1回:5通り
(1)5C1=5
●2回:14通り
(2)4C1=4 (1,1)5C2=10
●3回:29通り
(3)3C1=3 (2,1)4C1×4C1=16 (1,1,1)5C3=10
●4回:49通り
(4)2C1=2
(3,1)3C1×4C1=12
(2,2)4C2=6
(2,1,1)4C1×4C2=24
(1,1,1,1)5C4=5
●5回:71通り
(5)1C1=1
(4,1)2C1×4C1=8
(3,1)3C1×3C1=9
(3,1,1)3C1×4C2=18
(2,2,1)4C2×3C1=18
(2,1,1,1)4C1×4C3=16
(1,1,1,1,1)5C5=1
●6回:90通り
(5,1)1C1×4C1=4
(4,2)2C1×3C1=6
(4,1,1)2C1×4C2=12
(3,3)3C2=3
(3,2,1)3C1×3C1×3C1=27
(3,1,1,1)3C1×4C3=12
(2,2,2)4C3=4
(2,2,1,1)4C2×3C2=18
(2,1,1,1,1)4C1×4C4=4
●7回:101通り
(5,2)1C1×3C1=3
(5,1,1)1C1×4C2=6
(4,3)2C1×2C1=4
(4,2,1)2C1×3C1×3C1=18
(4,1,1,1)2C1×4C3=8
(3,3,1)3C2×3C1=9
(3,2,2)3C1×3C2=9
(3,2,1,1)3C1×3C1×3C2=27
(3,1,1,1,1)3C1×4C4=3
(2,2,2,1)4C3×2C1=8
(2,2,1,1,1)4C2×3C3=6
●文句の総数8〜15回に関してだが、
総文句k回の並び方の、左右を逆にすれば、文句15−k回となるので割愛。
例:
213456…文句1回
654312…文句14回
6人の並び方は、6!=720通りであるが、先ほど述べた並べ方の総数も
(1+5+14+29+49+71+90+101)×2=720となり、これに等しい。
◆富山県 萩の葉 さんからの解答
6年生は文句を言わない
5年生は0または1回文句を言う
4年生は0,1または2回文句を言うのでここまでの合計は
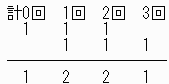 通りある
通りある
3年生は0,1,2,3回文句を言うのでここまでの合計は
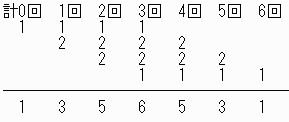 通りある
通りある
2年生は0,1,2,3,4回文句を言うのでここまでの合計は
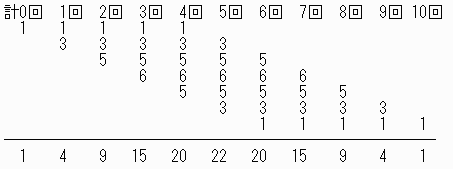 通りある
通りある
1年生は0,1,2,3,4、5回文句を言うのでここまでの合計は
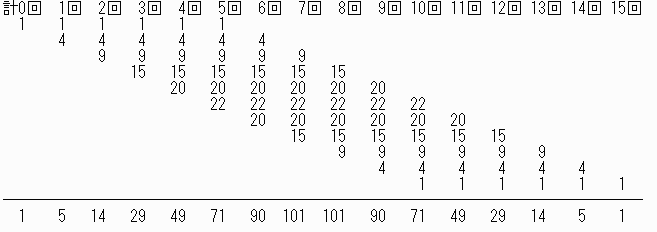 通りある
通りある
よって文句5回は71通り、6回は90通り、7回は101通りで6人の並び方は総計720通りある
◆ 問題へもどる
◆ 今週の問題へ