『今週の問題』

『今週の問題』第167回　解答

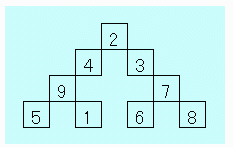
◆愛知県　Y.M.Ojisan　さんからの解答

【問題１】

図中 4,9,5 位置と　3,7,8位置の２乗和は等しい。
₉C₃=84 の組み合わせから２乗和が等しくかつ数字がダブらない組み合わせを探すと下記の６組である。

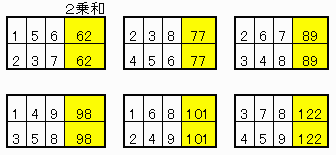
図中　4,9 や　3,7　 1,6 に入る数字の組み合わせは　₉C₂=36 通りあるが、それらは少なくとも　上表の２箇所に現れなければならず、そのような組み合わせは次の８組である。

1,6 2,3 2,7 3,7 3,8 4,5 4,9 5,6

これらの中から３組選んで、必要条件を満たすものを探すと次の２組である。

（１，６）－（３，７）－（４，９）と　（２，７）－（３，８）－（５，６）　

後者は総合計が３の倍数にはならず条件を満足できない。
結局　頂点が（２，５，８）で辺上が前者組み合わせであるものだけが解である。

【問題２】

線形和もすべて２０に等しい。

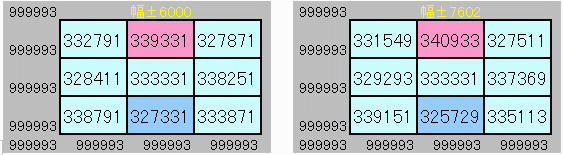
【おまけ】

中心は３３３３３１である。
３３３３３１±Xが素数であるXをリストアップし、
ｐ,ｑ∈X集合,ｐ＋ｑ , ｐ－ｑ∈X集合を探索

◆栃木県の中学校３年生　KENちゃん（悟）さんからの解答

【問題１】

わかりやすく累乗した後の数で考えてみると、？には

1・4・9・16・25・36・49・64・81

の数が一つずつ入ることがわかります。

一辺の数の和の求め方

9つの数の和は、285。
そこに9つの数のうち3つの数をさらに足しますが（端の数は二回足すため）、足す3つの数の和は3で割り切れないといけません。
（285にその数を足して3で割り切れないと一辺の数の和が自然数じゃなくなってしまうから。）

9つの数を小・中・大の三グループに分けてみる。

小（1・4・9）　中（16・25・36）　大（49・64・81）　となる。

各グループの左の数、中の数、右の数同士を足すと3で割り切れる数になることがわかる。

1+16+49＝66（66÷3＝22）
4+25+64＝93（93÷3＝31）
9+36+81＝126（126÷3＝42）

証明

それぞれのグループの数を元に戻して考えると、
小（1・2・3）　中（4・5・6）　大（7・8・9）　となり、左の数、中の数、右の数いずれも
小→中→大＝ｎ→ｎ+3→ｎ+6　という関係になっていることがわかる。

ここから式を立てると

　ｎ²+（ｎ+3）²+（ｎ+6）²
＝ｎ²+ｎ²+6ｎ+9+ｎ²+12ｎ+36
＝3ｎ²+18ｎ+45　　因数分解すると
＝3（ｎ²+6ｎ+15）

つまり3で割り切れる数になる。（ｎは1から3までの自然数）

ここでは一辺の数の和を求めるので、平均の値が必要となる。
つまりここでは（4・25・64）の3つの数を端の数とする。

すると一辺の和は　（285+4+25+64）÷3＝126　となる。

後は残りの数をうまく当てはめればいい。
（1・9・16・36・49・81をすべて使う）

4・25の辺は97足りない→97＝16+81
4・64の辺は58足りない→58＝9+49
25・64の辺は37足りない→37＝1+36

数字を元に戻すと

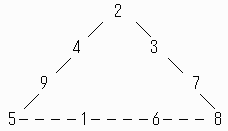
の形になる。

【問題２】

それぞれの数を二乗して足さなくても、各辺の数の和は等しい。

2+4+9+5＝20
2+3+7+8＝20
5+1+6+8＝20

◆鹿児島県の中学校３年生　31070W.K　さんからの解答

【問題１】

各列の合計が等しいのだから、3列の合計数は、3の倍数になります。
1から9までの２乗をすべて足すと、285で3の倍数です。
つまり、各列で共有される、三角の数の２乗の和は、３の倍数になる必要があります。

その可能性があるのは、全部で２１通りあります(図１）。

その２１通りのそれぞれで、２乗の和を２８５にたしたものを３で割りました。
この数をXとします。
Xは最小で１０２、最大で１４１ということがわかったので、９の２乗である８１が入りうるものを求めたらいいのではないのかと思い、２１通りのXから、それぞれ８１を引いたものをまとめました（A)。

また、１から８の乗数のうち、３つをたしたものを、図にまとめました（B)。

（A)と（B)のうち等しいものは、７通りあり、それらを順番に調べていくと、答えは、上から時計回りに、次のようになりました。

答え２，３，７，８，６，１，５，９，４

(A)と（B）のうち、等しいもの

21,29,41,42,45,49,53,56

【問題２】

各列の和が、２０になる。不思議です。

◆大阪府の高校生　Alpha Omega　さんからの解答

【問題１】

「?」の部分を

            a
          ／ ＼
        i       b
      ／          ＼
    h               c
  ／                  ＼
g ----- f ----- e ----- d

とおく。

ただし対称性を考えて、a＜d＜g , b＜c , e＜f , h＜i とする。
また、1辺の数の2乗の和をSとおく。

すると、

3S=(a²+b²+c²+d²+e²+...+i²)+(a²+d²+g²)
=(1²+²²+3²+...+9²)+(a²+d²+g²)
=285+(a²+d²+g²)

したがって、

S=95+(a²+d²+g²)/3

Sが整数であるためには、(a²+d²+g²) が3で割り切れなければならない。

ところである整数Nについて、
Nを3で割った余りとN²を3で割った余りとの関係を考えると、

Nが3で割り切れるとき、N²も3で割り切れる。
Nを3で割ったときの余りが1のとき、N²も1余る。
Nを3で割ったときの余りが2のとき、N²は1余る。

以上のことがいえるので、

a,d,gはすべて3で割り切れる、すなわち(a,d,g)=(3,6,9) であるか、あるいはどのa,d,gも3で割り切れない。

というふうに条件を絞り込めることができる。また、

a²+b²+c²+d² = S → b²+c² = S-(a²+d²) ...(1)

d²+e²+f²+g² = S → e²+f² = S-(d²+g²) ...(2)

g²+h²+i²+a² = S → h²+i² = S-(g²+a²) ...(3)

である。

a,d,gについて考えられるすべての数の組み合わせとそれに対する(1),(2),(3)の値を表にしたのが表Ⅱである。
表Ⅰは2つの平方数の和を示している。

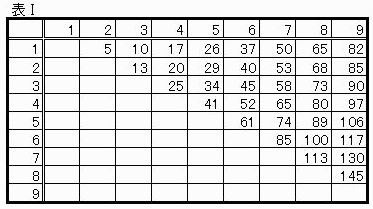
(1),(2),(3)の値が表Ⅰに存在するか調べる。
(1),(2),(3)の値すべてが表Ⅰに存在するとき以外は、a～iの中で整数でないものが必ず存在する。
これにより候補を絞り込める。(表Ⅱの青の部分が候補)

絞り込んだ値をさらに詳しく調べる。

(a,g,d)=(1,2,4)のとき、表より(b,c)=(4,9) →4が重複するので不適

(a,g,d)=(1,2,8)のとき、(b,c)=(7,8) →不適

(a,g,d)=(2,5,8)のとき、
(b,c)=(4,9) , (e,f)=(1,6) , (h,i)=(3,7) →適

(a,g,d)=(4,5,8)のとき、(b,c)=(5,8) →不適

(a,g,d)=(4,7,8)のとき、(b,c)=(3,8) →不適

したがって

(a,b,c,d,e,f,g,h,i)=(2,4,9,5,1,6,8,3,7) すなわち、

            2
          ／ ＼
        7       4
      ／          ＼
    3               9
  ／                  ＼
8 ----- 6 ----- 1 ----- 5

のときのみ。

【問題２】

1辺の2乗の和が等しいだけでなく、単に1辺の和についても等しいことがわかる。

【おまけ】

答えは分かりませんでしたが、以下のようなことが分かりました。

魔法陣に入れる数の一の位に注目する。
すべて素数なので、一の位の数字は1,3,7,9の4つに限られる。
条件より数の和は10⁶-7なので一の位の数字は3である。
すなわち、1,3,7,9の4つの数字を使うち、3つを使って(重複を許可)その合計の値の一の位の数字が3となるようにしなければならない。

その組み合わせは、

(1,1,1),(1,3,9),(3,3,7),(7,7,9)の4つ。
これを以下の手順で魔法陣に配置する。

(1)上の4つの組からうまく2組選び出しＸ状に配置する

? ?
 ?
? ?

(2)穴の空いている部分を順次埋めていく
(3)矛盾の発生しないものが答えの候補。

すべての場合を調べると、

111
111
111

の場合に限定される。

つまり、条件に合う素数は一の位の数字が「1」であるものだけである。

◆千葉県の大学生　きよっぴ　さんからの解答

【問題１】

まず、使える整数のうち、偶数は２、４、６、８の４つ、奇数は１、３、５、７、９の５つである。

偶数を2n、奇数を2n+1とおき、それらの二乗について４を法とする剰余系を考えると、

偶数：(2n)² ＝ 4n² ≡ 0 (mod.4)
奇数：(2n+1)² ＝ 4(n²+n)+1 ≡ 1 (mod.4)

となる。

４つの数の二乗が各辺で一致するには、まず剰余が一致しなければならない。

1)　各辺の剰余が０である場合。
　それぞれの辺の４数が、すべて偶数か、すべて奇数でなければならないが、それは絶対に不可能。

2)　各辺の剰余が１である場合。
　それぞれの辺で、偶数が３つ、奇数が１つであればよいが、それは偶数が足りず不可能。

3)　各辺の剰余が２である場合。
　それぞれの辺で、偶数、奇数が２つずつであればよい。
それは、２つの頂点を偶数にし、その２頂点に挟まれない辺に１つずつ偶数を置いたときのみ可能である。

4)　各辺の剰余が３である場合。
　それぞれの辺で、偶数が１つ、奇数が３つなければならないが、それは奇数が足りず不可能。

☆よって、各辺の４を法とする剰余はすべて２であり、頂点のうち２つは偶数で、１つは奇数である。

次に全ての辺の二乗の合計を考える。
１～９は必ず一回は使われ、頂点の数字は２回使われるので、

1²+2²+3²+4²+5²+6²+7²+8²+9² ＝ 285 に頂点の二乗が加わる。

　また三辺の二乗の合計が一致するので、全ての辺の二乗の合計は３で割り切れなければならない。

ここで、３の倍数3n、３で割って１余る数3n+1、２余る数3n+2について、それぞれの二乗の３を法とする剰余系を考えると、

３の倍数：(3n)² ＝ 9n² ≡ 0 (mod.3)
１余る数：(3n+1)² ＝ 3(3n²+2n)+1 ≡ 1 (mod.3)
２余る数：(3n+2)² ＝ 3(3n²+4n+1)+1 ≡ 1 (mod.3)
である。

また、285 ≡ 0 (mod.3) である。
つまり、285と３頂点の二乗の和が３の倍数になるには、

1)　３頂点すべてが３の倍数である場合。
2)　３頂点すべてが３の倍数以外である場合。

の２つが考えられるが、1)は☆より２頂点が偶数であることから不可能である。
（偶数で３の倍数は６のみ）

★よって、３頂点に来るのは３の倍数以外の数である。

以上より☆と★から、考えられる頂点の数の組合せは、
｛１、５、７｝から１つと、｛２、４、８｝から２つを使う場合の、９通りである。

それぞれの場合について、合計と可能な組合せを考えていく。

a)　頂点が（１、２、４）の場合。
すべての二乗の合計は 285+1+4+16 = 306 で、１辺の二乗の合計は102。
１と２に挟まれる２数の二乗の合計は 102-(1+4) = 97 だが、残りの数でこれをみたすものはない。

b)　頂点が（１、２、８）の場合。
すべての二乗の合計は 285+1+4+64 = 354 で、１辺の二乗の合計は118。
１と２に挟まれる２数の二乗の合計は 118-(1+4) = 113 だが、残りの数でこれをみたすものはない。

c)　頂点が（１、４、８）の場合。
すべての二乗の合計は 285+1+16+64 = 366 で、１辺の二乗の合計は122。
１と４に挟まれる２数の二乗の合計は 122-(1+16) = 105 だが、残りの数でこれをみたすものはない。

d)　頂点が（５、２、４）の場合。
すべての二乗の合計は 285+25+4+16 = 330 で、１辺の二乗の合計は110。
５と２に挟まれる２数の二乗の合計は 110-(25+4) = 81 だが、残りの数でこれをみたすものはない。

e)　頂点が（５、２、８）の場合。
すべての二乗の合計は 285+25+4+64 = 378 で、１辺の二乗の合計は126。
５と２に挟まれる２数の二乗の合計は 126-(25+4) = 97 で、（４、９）がこれをみたす。
５と８に挟まれる２数の二乗の合計は 126-(25+64) = 37 で、（１、６）がこれをみたす。
２と８に挟まれる２数の二乗の合計は 126-(4+64) = 58 で、（３、７）がこれをみたす。

これは求める解の条件を満たす。

f)　頂点が（５、４、８）の場合。
すべての二乗の合計は 285+25+16+64 = 390 で、１辺の二乗の合計は130。
５と４に挟まれる２数の二乗の合計は 130-(25+16) = 89 だが、残りの数でこれをみたすものはない。

g)　頂点が（７、２、４）の場合。
すべての二乗の合計は 285+49+4+16 = 354 で、１辺の二乗の合計は118。
７と２に挟まれる２数の二乗の合計は 118-(49+4) = 65 だが、残りの数でこれをみたすものはない。

h)　頂点が（７、２、８）の場合。
すべての二乗の合計は 285+49+4+64 = 402 で、１辺の二乗の合計は134。
７と２に挟まれる２数の二乗の合計は 134-(49+4) = 81 だが、残りの数でこれをみたすものはない。

i)　頂点が（７、４、８）の場合。
すべての二乗の合計は 285+49+16+64 = 414 で、１辺の二乗の合計は138。
７と４に挟まれる２数の二乗の合計は 138-(49+16) = 73 だが、残りの数でこれをみたすものはない。

よって、求める解はe)のときのみで、

　　　　　　５
　　　　　／　＼
　　　　９　　　１
　　　／　　　　　＼
　　４　　　　　　　６
　／　　　　　　　　　＼
２－－－３－－－７－－－８

である。

【問題２】

二乗の和だけでなく、一乗の和（そのままの数）の和も、各辺で等しくなっている。

また並べ方にもよるが、３を法として合同な組
｛１、４、７｝、｛２、５、８｝、｛３、６、９｝が１２０°回転対称な位置にある。ちょっと綺麗かも。

◆広島県の大学生　うとんた　さんからの解答

【問題１】

            ５       
          ／  ＼      
        ９　　　１     
      ／　　　　　＼    
    ４　　　　　　　６
  ／　　　　　　　　　＼  
２ ―― ３ ―― ７ ―― ８

●
まず１～９を二乗して、全て足すと、
∑1/2・n(n+1)(2n+1)より、285が出る。

285は3で割り切れる数であることを確認する。―(1)

●
ここで、それぞれの２乗の数を３で割った時の余りにより

Ａ＝{１、２、４、５、７、８}　（余り１）
Ｂ＝{３、６、９}　（余り０）

に分ける。

●
三角形の頂点、すなわち重複分について考えると、(1)より、頂点の合計は３で割り切れなければならない。

よってＡが３つ、もしくはＢが３つのときのみ、成立する。
Ｂが三つの場合について、具体的に考えてみる。
(285+3²+6²+9²)÷3=137

３と９を頂点とした辺において、合計137は成り立たない。
よってこれは不適。

つまりＡが三つの頂点にある場合に成り立つ事がわかる。―(2)

●
さて、一辺における数の合計は

【３で割り切れる】
【３で割って１余る】
【３で割って２余る】

の三パターンだが、(2)から頂点は全てＡなので、各辺の合計が全て同じパターンとなるためには
・３で割り切れるしか考えられない―(3)
・Ｂは、各辺に一つずつあり、二つ以上が存在する事はない　―(4)

事がわかる。

★
ここで、図を書き（割愛）Ｂの数字を各辺に固定して考える
図なしの説明のため、３を含む辺をＸ、６を含む辺をＹ、９を含む辺をＺ、と仮におく。

●
辺Ｚについて考えてみると、３辺の合計は高々４２３である。
これは頂点に８、７、５と最大の数が配置された場合である事を加味して考えると、辺Ｚには、８も７も存在しえない事が分かる。―(5)

●
ここで、一辺における数の合計は奇数もしくは偶数である。
奇数となる組み合わせは
（?@）奇・奇・奇・偶
（?A）奇・偶・偶・偶

偶数となる組み合わせは
（?B）奇・奇・奇・奇
（?C）奇・奇・偶・偶
（?D）偶・偶・偶・偶

であるが、１～９の中には偶数が４つに奇数が５つである事と、(4)から、
?Bと?Dの組み合わせはありえない。―(6)

●
（１）各辺の合計が奇数になるとする

辺Ｚに存在しえるのは、(5)から１、２、４、５であるので、
?@の組み合わせ、すなわち１、５、９、（２もしくは４）となる。
この合計は、１１１か１２３である

これを３倍して285から引いた数字が頂点の合計となるが、４８および８４は、７と８の配置を加味して考えると、当てはまらない事になる。

よって各辺の合計は奇数とはならない。

（２）各辺の合計が奇数になるとする

(6)より、各辺には奇数と偶数がそれぞれ２つずつ配置されているので、
（１）と同様に考え、辺Ｚの組み合わせは
２、４、９、（１または５）となる
この合計は１０２か１２６である。

これを3倍して285から引いた数字、頂点の合計は２１、９３となるが、辺Ｚの対頂角の頂点部分には、５、７、８のいずれかが来ることから、前者はなりたたない。

よって辺Ｚの組み合わせは２、４、５、９となる。

●
頂点の合計は９３となったわけであるが、辺Ｚの両端の頂点の合計は高々４１なので、残りの頂点、すなわち辺Ｚの対頂角部には、８が入る。

●
辺Ｙについて見ると、６と８が存在している事から、既に合計は100となっている。
つまり７は入らず、１が入る事になる。
126-1-100=25
よって辺Ｙの組み合わせは
５→１→６→８

●
辺Ｘの残りの数字は、
126-（9+49+64）=4

よって辺Ｘの組み合わせは
２→３→７→８

以上より、最初に述べた答えが求められた。

【問題２】

・二乗せずそのまま足しても、等式が成立する
・頂点の数字は、３で割ると２余る

◆埼玉県　たまちゃん　さんからの解答

各辺の自乗和は、126

上記三角形の頂点の自乗数を X Y Z とし、辺上の自乗数をA B C D E F とする。

     X
   A   F
 D     C
Y  B E  Z

{X Y Z A B C D E F} = {1 4 9 16 25 36 49 64 81}

とすると、以下の式にモデル化できる。

X + A + D + Y = P
Y + B + E + Z = P
Z + C + F + X = P

また、次の性質を使用する。

性質1
自然数の自乗数の3の剰余は、元の数が3の倍数の時0、それ以外は1となる。

つまり、{9 36 81}は3で割り切れ、{1 4 16 25 49 64}を3で割ると1余る。

上記のモデル化した３式の辺々を加えると以下となる。
(X + Y + Z) + X + Y + Z + A + B + C + D + E + F = 3P

ここで、X + Y + Z + A + B + C + D + E + F は、1 4 16・・・81の和と等しく285となる。

これより、

X + Y + Z + 285 = 3P
X + Y + Z = 3P -285 = 3(P - 95)

となり、X + Y + Z が3の倍数であることが解る。

ここから、X Y Z の組合せは、{9 36 81} か{1 4 16 25 49 64}の任意の3つ　のいずれかとなる。
後者は、全ての数が3で割って1余るため、3つを加えると3の倍数となるためである。

まず、{X Y Z} = {9 36 81}として、実際に数を総当りで当てはめると、いずれの場合も答に至らないことが解る。

これより、{X Y Z}は、{1 4 16 25 49 64}の任意の3つが候補となる。
この時点で、{X Y Z}は、6個から3個を抽出する組合せで20通りとなる。

次に、{9 36 81}がA B C D E Fにどのように配置されるかを考える。

例えば、A = 9 D = 36 B = 81 とすると、上記３式は、

X + 9 + 36 + Y = P
Y + 81 + E + Z = P
Z + C + F + Z = P

となるが、最初の式の左辺を3で割ると余りは2となる(X Yを3で割ると1余るため)が、２番目の式は3で割り切れ、3番目の式は3で割って1余る。

これより、{9 36 81}は各式に1つずつ配置されなければならない。

以上を整理して、改めてモデル化3式を書き直すと

X + A + 9 + Y = P --- (1)
Y + B + 36 + Z = P　--- (2)
Z + C + 81 + X = P　--- (3)

となる。

上記(1)(2)(3)の左辺を、再度3の剰余で考えると、
例えば(1)では、X A Y が余り1のため、左辺は、3で割り切れることが解る。

(2)(3)も同様である。
このことから、Pは3の倍数であることが解る。

一方、先の式で、X + Y + Z + 285 = 3P　であったが、Pが3の倍数のため、
X + Y + Z + 285は、9の倍数となる。

この性質を利用して{X Y Z}を絞り込むと、以下の8通りに絞られる。

さらに、{X Y Z}が全て偶数とすると、{A B C}は全て奇数になる。

これを(1)(2)(3)式にあてはめると、

偶 + 奇 + 9 + 偶 = P ---(1)
偶 + 奇 + 36 + 偶 = P ---(2)
偶 + 奇 + 81 + 偶 = P ---(3)

となるが、(2)式のみ左辺が奇数となり、当てはまらない。
{X Y Z}が全て奇数の時も同様である。

これらのパタンを除くと、上記8通りは、次の6通りに絞られる

ここからは、総当戦で調べる。

{X Y Z}が偶数、偶数、奇数の組合せの場合、

偶 + 奇 + 9 + 偶 = P ---(1)
偶 + 奇 + 36 + 奇 = P ---(2)
偶 + 偶 + 81 + 奇 = P ---(3)

または、

偶 + 偶 + 9 + 奇 = P ---(1)
偶 + 奇 + 36 + 奇 = P ---(2)
偶 + 奇 + 81 + 偶 = P ---(3)

が、成立するパターンである。
(これ以外は、(1)(2)(3)式の左辺の偶数・奇数が同じにならない)

どちらのパターンでも(2)式は同じであるため、(2)式を利用して

Y + B + 36 + Z = P　--- (2)

Yには、２つの偶数のいずれか、Bには、２つの奇数をいずれかを入れてためせば良いので、(2)式の検証は、各通りに対して4回行なえばよい。

後は、(2)式が成立した時の残った数字で(1)が成立するかどうかを当てはめて見ればよい。

この結果、成立するパターンは、次の１とおりとなる。

 X	Y	Z		 P
 2	5	8		126

◆千葉県　トリガラJr　さんからの解答

問題は１～９の２乗と書いてありましたが
ここでは1,4,9,16･･･64,81を使って話を進めます．

三角形の３頂点をＸ，Ｙ，Ｚとする．
またＸ，Ｙ，Ｚに入る数もＸ，Ｙ，Ｚで表すものとする．

（辺ＸＹの和）＋（辺ＹＺの和）＋（辺ＺＸの和）
＝１＋４＋９＋・・・＋８１＋Ｘ＋Ｙ＋Ｚ＝２８５＋Ｘ＋Ｙ＋Ｚ･･･(1)

（辺ＸＹの和），（辺ＹＺの和），（辺ＺＸの和）は等しいことより(1)は３の倍数．

よって，２８５が３の倍数なので，Ｘ＋Ｙ＋Ｚは３の倍数　･･･?@

また一辺の和は（２８５＋Ｘ＋Ｙ＋Ｚ）／３･･･?A

ここで１，４，･･･，８１を９の剰余で分類する

Ａ｛９，３６，８１｝　　割り切れる
Ｂ｛１，６４｝　　　　　余り１
Ｃ｛４，４９｝　　　　　余り４
Ｄ｛１６，２５｝　　　　余り７

さらにＡは３の倍数であり，Ｂ，Ｃ，Ｄはいずれも３で割ると１余る．

?@よりＸ，Ｙ，Ｚに入る数はＡから３個，またはＢ，Ｃ，Ｄから３個のいずれか．

a-1)
Ｘ，Ｙ，ＺにＡから３個いれるとする．Ｘ＝９，Ｙ＝３６，Ｚ＝８１とする．
?Aより一辺の和は１３７．辺ＸＹの中２個の和は
１３７－（９＋３６）＝９２．
これを満たす２数存在しないのでＸ，Ｙ，ＺにＡから３個ではない．

a-2)
よってＸ，Ｙ，ＺはＢ，Ｃ，Ｄから３個選ばれる．
各辺の和を３で割ったあまりを考えることで各辺の中２個はそれぞれＡから１個，Ｂ，Ｃ，Ｄから１個．

a-3)
Ｘ，ＹがＢの要素とする

a-3-1)
辺ＸＹの中２個をＡから１個，Ｃから１個とすると辺ＸＹの和を９で割ったあまりは６．
Ｃの残り１個，Ｄの２個のうちどれをＺに入れても辺ＸＺ，辺ＹＺの少なくとも一方はＡ，Ｂ，Ｃ，Ｄから１個ずつになる．
それを９で割ったあまりは３．
辺ＸＹに一致しない．

a-3-2)
辺ＸＹの中２個をＡから１個，Ｄから１個とすると辺ＸＹの和は９で割り切れる．
Ｄの残り１個，Ｃの２個のうちどれをＺに入れても辺ＸＺ，辺ＹＺの少なくとも一方はＡ，Ｂ，Ｃ，Ｄから１個ずつになる．
それを９で割ったあまりは３．
辺ＸＹに一致しない

a-4)
Ｘ，ＹがともにＣの要素，ともにＤの要素のときもa-3)と同様．

a-5)
よってＸ，Ｙ，ＺはＢ，Ｃ，Ｄから各１個ずつ．

１，４，･･･，８１は偶数４個，奇数５個

b-1)
Ｘ，Ｙ，Ｚすべて偶数とする．
残り１個の偶数が入る辺は和が奇数，残り２辺は和が偶数で，各辺の和が一致しない．

b-2)Ｘのみ偶数とする．
辺ＸＹと辺ＹＺの中２個に入る偶数の個数は等しく，ＺＹの中２個に３個の偶数は入らないことから残りの偶数は各辺に１個ずつ入る．
このとき辺ＸＹの和は偶数，辺ＹＺの和は奇数で一致しない．

b-3)
Ｘ，Ｙ，Ｚすべて奇数とする．
Ｘ＝１，Ｙ＝２５，Ｚ＝４９とする．
?Aより一辺の和は１２０．
辺ＸＹの中２個の和は１２０－（１＋２５）＝９４．
これをみたす２数は存在しない．

b-4)
よってＸ，Ｙ，Ｚは偶数２個，奇数１個

a-5),b=4)より
（Ｘ，Ｙ，Ｚ）＝（６４，４，２５），（４，１６，１），（１６，６４，４９）
のいずれか．

c-1)
（Ｘ，Ｙ，Ｚ）＝（６４，４，２５）とする．
?Aより一辺の和は１２６．
辺ＸＹの中２個の和は，１２６－（６４＋２５）＝５８
これをみたす２数は９，４９．
同様にして辺ＹＺの中２個は１６，８１，辺ＺＸの中２個は１，３６．

c-2)
（Ｘ，Ｙ，Ｚ）＝（４，１６，１）とする．
?Aより一辺の和は１０２．
辺ＸＹの中２個の和は，１０２－（４＋１６）＝８２
これをみたす２数は残りの数にはない．

c-2)
（Ｘ，Ｙ，Ｚ）＝（１６，６４，４９）とする．
?Aより一辺の和は１３８．
辺ＸＹの中２個の和は，１３８－（１６＋６４）＝５８
これをみたす２数は残りの数にはない．

よって解はc-1)のパターンに，一意に決まる．

このセットはもとの１，２，３･･･９でも各辺の和が一致するのですね．

◆東京都　明　さんからの解答

【問題１】

回転、裏返し、辺の２数の交換による違いを無視すると下記の一通りです。

　　　2
　　4   7
　9       3
5   1   6   8

下記プログラムで総当りをしました。
（１０進ＢＡＳＩＣです。）
結果は1つの頂点を始めとし、順に数値を割り当てます。

結果
No. 1 2 4 9 5 1 6 8 3 7

-------------------------

DECLARE EXTERNAL SUB ZYUN
DIM N(9)
DIM D(9)
LET M=2       !2乗を指定
LET C=0
DATA 1,1,1,2,2,3,3,4,4
MAT READ N

DO
   LET D1=0
   LET D2=0
   LET D3=0
   LET D4=0
   LET Y1=0
   LET Y2=0
   LET Y3=0
   FOR J=1 TO 9
      LET Z=J^M
      SELECT CASE N(J)
      CASE 1
         LET D1=D1+1
         SELECT CASE D1
         CASE 1
            LET Y1=Y1+Z
            LET Y3=Y3+Z
            LET D(1)=J 
         CASE 2
            LET Y1=Y1+Z         
            LET Y2=Y2+Z
            LET D(4)=J
         CASE 3
            LET Y2=Y2+Z
            LET Y3=Y3+Z
            LET D(7)=J
         END SELECT
      CASE 2
         LET Y1=Y1+Z
         LET D(2+D2)=J
         LET D2=D2+1
      CASE 3
         LET Y2=Y2+Z
         LET D(5+D3)=J
         LET D3=D3+1
      CASE 4
         LET Y3=Y3+Z
         LET D(8+D4)=J
         LET D4=D4+1
      END SELECT
   NEXT J
   IF Y1=Y2 AND Y2=Y3 THEN
      LET C=C+1
      PRINT "No.";C,
      FOR J=1 TO 9
         PRINT D(J);
      NEXT J
      PRINT
   END IF
   CALL ZYUN(9,EX,N)
   IF EX=0 THEN EXIT DO
LOOP
IF C=0 THEN PRINT "解なし"
END

!順列の変更
EXTERNAL SUB ZYUN(K,EX,N())
DECLARE EXTERNAL SUB SEIRETU
LET EX=0
LET J=1
DO
   IF J>=K THEN EXIT DO
   IF N(K-J)<N(K-J+1) THEN
      CALL SEIRETU(J,K,N)
      LET L=1
      DO
         IF N(K-J)>=N(K-J+L) THEN 
            LET L=L+1
         ELSE
            LET B=N(K-J)
            LET N(K-J)=N(K-J+L)
            LET N(K-J+L)=B
            LET EX=1
            EXIT DO
         END IF
      LOOP
      EXIT DO
   ELSE 
      LET J=J+1          
   END IF
LOOP
END SUB

!配列の整列
EXTERNAL  SUB SEIRETU(J,K,N())
LET D=K-J+1
LET E=K
DO WHILE D<E
   LET B=N(D)
   LET N(D)=N(E)
   LET N(E)=B
   LET D=D+1
   LET E=E-1
LOOP
END SUB

-----------------------------------

【問題２】

気がつくこと。

1.各辺の和が共に20。

2.数値を正三角形上に配置したとき、「5」を頂点とする２等辺三角形の頂点の和がすべて15。

3.したがって3×3の魔方陣の配置と何らかの対応が見られる。

8　1　6
3　5　7
4　9　2

バランスをとるという意味では、当然似た性質が出てくるのでしょうが、論理的なつながりの有無まではわかりませんでした。

なお余計ですが、各辺の和が等しい配列は、プログラムのM=1として18種類の基本形が見つかりました。
ついでに、立方和以上では解がありませんでした。

（9⁶ ＞8⁶ + 7⁶ + 6⁶+ 5⁶から6乗和以上は解なし。プログラムで5乗和まで、解なしを確認。）

【おまけ】

327871　338251　333871　　
　
339331　333331　327331
　　　　　　　　
332791　328411　338791

N=10⁶-7として、中心をcとして、cを通る、縦、横、斜めの4つの列を加算することにより
4N　=　3N　+　3c　を得る

よって、c　=　N/3　=　333331（これは素数のはず）

縦、横、斜めが等しいことにより、変数p 、q　として求める配列は、各項が素数であることを考えると下記のとおり。

c-(p+q)　c+2q　 c+(p-q）
c+2p　　　c　　 c-2p
c-(p-q） c-2q　 c+(p+q)

以上からc+2x ,c-2xが共に素数となる2xをリストアップし、上記条件に合う最小の数値を探しました。

以下に素数の洗い出しプログラムと、条件に合う最小値の検出プログラムを示します。

-----------------------------------------

REM 素数の洗い出し
LET C=0
LET LC=0
FOR L=2 TO 333330 STEP 2
   LET N=333331+L
   CALL SOSUU(N)
   IF S=1 THEN
      LET N=333331-L
      CALL SOSUU(N)
      IF S=1 THEN
         LET LC=LC+1
         LET C=C+1
         SELECT CASE LC
         CASE 1
            PRINT "DATA ";L;
         CASE 5
            LET LC=0
            PRINT ",";L
         CASE ELSE
            PRINT ",";L;
         END SELECT
      END IF
   END IF
NEXT L
PRINT "総数 : ";C  
STOP

!素数/合成数のチェック
SUB SOSUU(K) 
   LET S=1
   IF K=2 THEN EXIT SUB
   IF K=3 THEN EXIT SUB
   LET S=0
   IF K=1 THEN EXIT SUB
   IF MOD(K,2)=0 THEN EXIT SUB
   IF MOD(K,3)=0 THEN EXIT SUB
   LET  M=INT(SQR(K))
   LET J=1
   DO WHILE 6*J-1<=M
      IF MOD(K,6*J-1)=0 THEN EXIT SUB
      IF MOD(K,6*J+1)=0 THEN EXIT SUB
      LET J=J+1
   LOOP
   LET S=1
END SUB

END
---------------------------------------
REM 検出プログラム
DATA  300 , 342 , 540 , 690 , 762 
DATA  858 , 1218 , 1320 , 1422 , 1512 
DATA  1530 , 1782 , 1830 , 1842 , 1992 
DATA  2118 , 2388 , 2478 , 2610 , 2892 
DATA  2922 , 3042 , 3132 , 3198 , 3312 
DATA  3468 , 3570 , 3858 , 3930 , 4038 
DATA  4122 , 4278 , 4350 , 4410 , 4542 
DATA  4788 , 4920 , 5082 , 5118 , 5352 
DATA  5442 , 5460 , 5508 , 5760 , 5772 
DATA  5820 , 6000 , 6042 , 6252 , 6348 
DATA  6468 , 6852 , 7008 , 7188 , 7248 
DATA  7392 , 7470 , 7518 , 7578 , 7602 
DATA  7608 , 7872 , 8112 , 8130 , 8238 
DATA  8310 , 8442 , 8520 , 8532 , 8742 
DATA  8880 , 9012 , 9120 , 9750 , 9822 
DATA  9888 , 9912 , 9972 , 10080 , 10200 

LET M=80
DIM N(M)
MAT READ N
FOR J=4 TO M
   FOR L=3 TO J-1
      LET R2Q=2*N(L)-N(J)
      LET RPQ=N(J)-N(L)
      LET IPQ=0
      LET I2Q=0
      FOR K=1 TO L-1
         IF RPQ=N(K) THEN LET  IPQ=1
         IF R2Q=N(K) THEN LET  I2Q=1
      NEXT K
      IF IPQ*I2Q=1 THEN
         PRINT "2p = ";N(J),"p+q = ";N(L),"2q = ";R2Q,"p-q = ";RPQ
         STOP
      END IF
   NEXT L
NEXT J 
PRINT "見つかりません"

END

------------------------------------

よくこのような問題を発想できますね。
尊敬！

　◆ 問題へもどる

　◆ 今週の問題へ

数学の部屋へもどる

『今週の問題』第167回 解答

『今週の問題』第167回　解答