◆滋賀県の中学校1年生 西尾 恭史 さんからの解答
【問題1−1】
先手が有利
【問題1−2】
(先手)・(後手、先手)・(後手、先手)・・・(後手、先手)、と分けて、
(後手)+(先手)=5の倍数にすれば勝てる
(付け加え)
1+2+3+・・・・・+20+21=22×11-11=231
231-5×A=B
(B=21以下の正の整数、A=正の整数)
A=42.43.44.45.46
B=21.16.11.6.1
(先手)=21.16.11.6.1を選び、上記の方法をとれば、必勝。
◆愛知県 Y.M.Ojisan さんからの解答
【問題1−1】
先手必勝
【問題1−2】
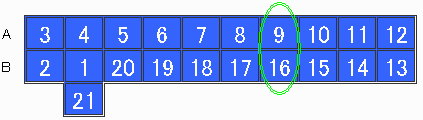
下図のように並べると、A行とB行の上下位置のものの和は全部5の倍数である。
よって、先手は21を取った後、後手がB行の数を選べば対応するA行の数を、A行のならB行の各ペアを選べば、最後の2枚はペアであり、5の倍数である。

【P.S.】
mod 5 で考えると 「0」〜「4」が各4個と「1」が5個である。
「1」グループと「4」グループ 、「2」グループと「3」グループ 、「0」
グループ内、というペアでも同じですから、適当にグループ内で選択して戦略を見にくくする手もあるでしょう。
問題のコンピュータ君は最初の「21」を除き、各グループ内で値の小さい方から選んでいるようです。
【問題2】
可能である。
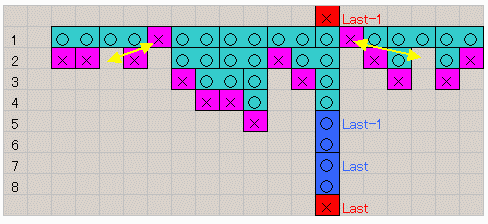
∵ 任意の個数nを並べることが出来るので、n=8の場合を図に示す。
戦略は下記です。
{ }内はn=8の値。
(1)縦にn個連続を目指します。
(2)私は、最初は横1行に2n-4{16}個を配置してゆきます。
こうするとコンピュータは最大でも2n-5{8}個しか縦列を防御できず、
無傷の縦列が最低2n-5{8}個残ります。
(3)私は無傷の縦列に対して2行目を追加して行きます。
コンピュータは(2)と同様にその半分2n-6{4}個しか防御できません。
(LAST-2)以上を繰り返して行くと最後に1列が生き残り、丸が縦にn−4個ならびます。
(LAST-1)私は最後の生き残り列に対して2個縦に接続します。
コンピュータは一方を封鎖できるのみです。(赤×)
(LAST)私は空いている側に2個縦に接続します。
以上でn個が縦に連続します。
【P.S.】
つぼが沢山あって、私は一回に2個のコインを1つ又は2つのつぼに入れます。
コンピュータは1回につき1つのつぼに蓋ができます。
という問題なら1裏表につきコインが1個増えた蓋無しつぼを1個作れるわけですから、簡単です。
マスになっていて縦でも横でもということで混乱させられました。
但しLASTの効率的手順は出てきませんが。
◆東京都 明 さんからの解答
【問題1−1】
問題1−2により先手有利(必勝)。
【問題1−2】
各数字を5で割った剰余でグループ分けする。
剰余1・・1,6,11,16,21
剰余2・・2,7,12,17
剰余3・・3,8,13,18
剰余4・・4,9,14,19
剰余0・・5,10,15,20
先手が勝つためには、1と4のグループ1枚ずつ、または2と3のグループ1枚ずつ、または0のグループ2枚でペアを組むカードを残せればよい。
先手が最初に1のグループ1枚を捨てれば、残りカードは丁度2枚合計が5で割り切れる10組のペアを組むことができる。
したがって、後手がいずれかを捨てたとき、先手は後手が捨てたカードのペアとなるカードを捨てて行けば、最後に残ったペアの合計は5で割り切れる。
【問題2】
次のようにすれば○を100個連続して並べることができる。
まず○を296個、マス目の互いに独立の位置(互いに干渉しない位置)にばらまく。
コンピューターが×で邪魔をできるのは高々半分の295個。
したがって残り295個には○を2つ並べられる。
これに対しコンピュータが×で邪魔できるのは294個。
したがって残り294個には○を3つ並べられる。
以下同様にコンピュータが邪魔をできない連珠に○を並べて行くと、最終的に96個の○が並んだ連珠が少なくとも1つ、×に邪魔されないで生き残る。
この連珠の両端に○を2つずつ加えれば100個の○を並べることができる。
(なお、マス目を行ごとに区切って一つの空間と考えれば、縦に並んだ○を独立な位置と考えることができる。)
問題2では生命の誕生のように、必然性があれば、わずかな可能性でも膨大な空間、時間の中で実現されるということを連想しました。
◆茨城県 雲隠才蔵 さんからの解答
【問題1−1】
先手必勝
【問題1−2】
1から21までの数を5で割った余りで分類すると、
グループ1:1,6,11,16,21
グループ2:2,7,12,17
グループ3:3,8,13,18
グループ4:4,9,14,19
グループ0:5,10,15,20
ゲームは先手が第一手を取った後、後手→先手を繰り返して、最後に先手で勝負が決まる。
先手が常に残った数の和が5の倍数になるような手を取りつづければ先手の勝ちとなる。
初手をグループ1から選ぶ(例えば21)と、残った20個の数の和は5の倍数となる。
その後はグループ1とグループ4、グループ2とグループ3、グループ0とグループ0を対応させて、後手が何を取っても、先手はそれに対応するグループから取れば残った数の和を5の倍数に維持できる。
(ここで、グループ0に属する数が偶数個あることが重要)
【問題2】
最短手ではないが、並べる数がいくつでも対応できる方法を示す。
先手:プレーヤー、後手:コンピュータとする。
先手が勝利する局面の最終形の例として次のように考える。
先手:×のあとに○が97個並んだ列2つに○を一個ずつ足して98個の列を2列作る。
後手:その2列のうち一方の列に×を置く。
先手:残ったほうの列に○を2個追加して100個にする。
先手勝利。
この直前の局面では、先手は○が97個並んだ列を作ることになるが、○が96個並んだ列に○を2個追加して98個の列とした場合、 後手に黒石を置かれてそれ以上○を伸ばせなくなってしまい列を損するだけである。
従って、○が96個並んだ列に○を1個ずつ追加して伸ばしていくことになる。
このとき、先手が2列を伸ばすごとに後手が1列を止めてしまうので、○96個の列は97個の列の必要数の2倍の数が必要である。
このように、○がM+1個並んだ列を作るにはM個の列が2倍の数必要になる。
そこで、石を100個並べるまでを、列の長さによって段階分けすると次のようになる。
第1段階:
先手は○を2個並べて配置する。
後手はその隣に×を置く。
これを充分な間隔を置いて2N回行う。
Nは後で求める。
第2段階:
○の長さ2の列を1ずつ伸ばす。
1手で2列が伸びるが、そのうち1列は後手によって止められる。
結局、2N-1手で、2N-1列が残る。
第3段階:
○の長さ3の列を1ずつ伸ばす。
1手で2列が伸びるが、そのうち1列は後手によって止められる。
結局、2N-2手で、2N-2列が残る。
:
:
第M段階(1<M<98):
○の長さMの列を1ずつ伸ばす。
1手で2列が伸びるが、そのうち1列は後手によって止められる。
結局、2N-M+1手で、2N-M+1列が残る。
:
:
第97段階:
○の長さ97の列を1ずつ伸ばして長さ98にする。
長さ97の列が2列あれば1手で長さ98の列が2列でき、そのうち1列が後手に止められる。
第98段階:
先手は長さ98の列に○2個を追加して長さ100にする。先手勝利。
先手の手数は、
(2N + 2N-1 + … + 2 + 1)+1
| = | n Σ m=0 |
2m | +1 |
| =2N+1 |
次にNを求める。
第97段階で、
2N-97+1=1
N-97+1=0
N=96
よって先手は297手(先手の手数)で勝つことが出来る。
石の長さLとして、L≧5では、
第一段階のN=L-4として、先手の手数2L-3手で勝つことが出来る。
なお、
L=1,2のとき:初手で先手の勝ち
L=3,4のとき:先手2手で勝ち。
ただし、Lが大きい場合上で述べた手順は最短手ではない。
L=100の場合で見ると、第1段階で○が横に2個並んだものを、縦に隙間無くつなげていくと、96手目には○が96個縦に並んだ列が2列出来上がる。
この2列は両端が空いているため、次に後手が一方を止めようとしても、先手は残ったほうの列に続く2手で4個の○を追加して勝つことが出来る。
従って後手は96手までに×を2個、縦の列を止められる位置に置く必要がある。
これは上で説明した充分な間隔をもって○を並べた場合に比べて後手は手が遅れている。
L=6の例
2N=26-4=22=4
先手:円数字 後手:漢数字

最短手は
![]()
【感想】
問題2は、盤が有限の場合どうなるか気になります。
たとえば100×100の場合、後手が100手で100個の×を互いに同じ行・列に存在しないように打てれば先手の勝ちはありません。
(どの行・列にも×が1個存在するので○は99個までしか置けない)
なおL=4で盤の大きさが4×4の時は先手必勝です。
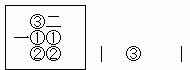
L=100で盤の大きさが100×100のときも先手必勝と言えるでしょうか?
また一般に長さLに対して盤の大きさL×Lのとき、常に先手必勝なのか、あるLを境に後手有利となるのか。
なんとなく、Lが大きいと後手有利な気もします。
◆ 問題へもどる
◆ 今週の問題へ