◆茨城県の中学校1年生 新五百円玉 さんからの解答
【問題1−1】
Aの方は2分の1で当たる
Bの方は,まず正解を「ア」と「a」だと仮定する。
選び方は4×4で16通りあり,
当たる場合は,初め「ア」を選んだ場合の4通りと,「ア」ではないものを選んだあとに「a」を選んだ場合の3通りで,確率は16分の7になる。
よってAのゲームの方が有利になる。
【問題1−2】
16分の7
【問題2】
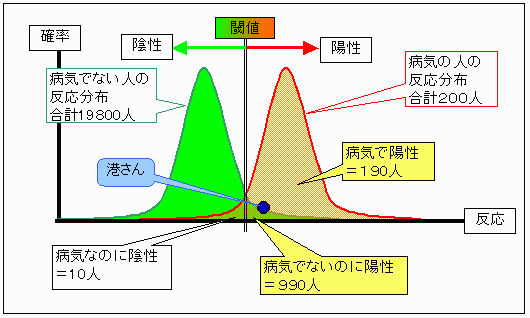
実際に正常な人は19800人いる。
また,実際に病気にかかっている人は200人いる。
正常な人のうち19800×5%の990人は病気にかかっていると診断される。
病気の人のうち200×95%の190人は病気にかかっていると診断される。
よって,実際に病気にかかっている確率は
190+990分の190=118分の19となる。
答えは118分の19
◆山梨県 Footmark さんからの解答
【問題1】
Aのゲームで賞品をもらえる確率=1/2。
Bのゲームで賞品をもらえる確率
=(1/4)+(3/4)*(1/4)=7/16
【問題1−1】
Aが有利。
【問題1−2】
7/16
【問題2】
病気である者が陽性となる人数 : 病気でない者が陽性となる人数
= (1x95):(99x5)
= 19:99
よって、
病気にかかっている確率
=19/(19+99)
=19/118
◆愛知県 Y.M.Ojisan さんからの解答
【問題1】
【問題1−1】
Bの方が損である。
Aの期待値は0.5である。
一方、単純にはBのほうの期待値は0.25×2=0.5で同じある。
しかし2回当たっても賞品は1個であるから、その分期待値が低下し、Bは損である。
【問題1−2】
0.4375
1/4+3/4*1/4=7/16<1/2
【問題2】
0.16101
正確さ=病気であって陽性の確率=病気でなくて陰性の確率=0.95
の意味とします。
[陽性] =[病気で陽性]+[病気でなくて陽性]
[病気で陽性]=200*0.95=190
[病気でなくて陽性]=(20000-200)*(1-0.95)=990
港さんが病気の確率=[病気で陽性]/ [陽性] =190/(190+990)=19/118=0.16101…

【正確さの別定義の場合1】
閾値が病気の側で3σ、すなわち病気である人を99.865%陽性とするように設定されている場合。
=0.16667
病気であって陽性の確率:p=0.99865≒1
正確さ≒(q*19800+p*200)/20000=0.95
の意味とします。ここでq:病気でなくて陰性の確率
よってq= 0.9495
[陽性] =[病気で陽性]+[病気でなくて陽性]
[病気で陽性]=200*0.99865=200
[病気でなくて陽性]=(20000-200)*(1-0.9495)=1000
港さんが病気の確率=[病気で陽性]/ [陽性] =200/(200+1000)=1/6=0.16666…
【正確さの別定義の場合2】
正確さの定義が陽性側だけで定義の場合=0.95
つまり
正確さ= [病気で陽性]/[陽性]=0.95
◆東京都 Q平 さんからの解答
【問題1】
1と2一緒に答えたほうが解答が楽なので一緒にします。
まず、Aで商品が貰える確率はそのまま 1/2 ある。
次にBで商品が貰える場合とその確率は、
1回目 2回目 当(1/4) ハズレ(3/4) 3/16 当(1/4) 当(1/4) 1/16 ハズレ(3/4)当(1/4) 3/16の3通りである。
1/2>7/16 なのでAのほうが有利であることが分かる。
【問題2】
A:検査で陽性、B:実際の病気であるとすると、
P(B)=0.01 P(A|B)=0.95 である。
ここで、ベイズの定理を使いたいんだが、
この場合のベイズの定理の形は Xの余事象をX\とすると、
P(B|A)= P(B)*P(A|B) / { P(B)*P(A|B) + P(B\)*P(A|B\) }
となる。
これに値を代入して行けばよいが、P(A|B\)の値が求まらない。
授業でやった問題を見てみると、更に後一つのデータが与えられていた。
感度と特異性、と言う表現をしていたが、両方が95%であると解釈して計算すると、
P(B|A)= 0.161となり、検査で陽性が出ても実際に病気である確率は 約16%なのであるので、港さんの考えは間違っていて、もうちょっと気楽に考えても良いよ、とアドバイスできる。
◆富山県 ヨーリー。 さんからの解答
【問題1−1】
とりあえず数量的な話をすると問題1−2まで突き抜けてしまうんでできるだけ理論的に 問題ででていた説に一つずつ考えていきます。
>1、Aの方は確率2分の1。
>Bの方は当たり2つに、はずれが6つもある。
>だからAの方がかなり有利だろう。
これについてはBコースの選択の仕方に問題があります。
一回目のボタンにはあたりが1つはずれが3つ、二回目のボタンにあたりが1つはずれが3つ。
この中でそこを押した時点で確実にはずれというボタンは二回目のはずれ三つしかありません。
というのは一回目のはずれのボタンは次に二回目のボタン郡から当たりを引けばいいということなのではずれというよりは「もう一回」ボタン。
話を総合するとあたり2つ、もう一回3つ、はずれ3つの計8個でこの理論では決定できません
>2、2回挑戦できるBの方がよさそうだ。
一見そのようにも見えますがBはAよりも当たりを引く確率ははるかに低く、この理論でも決定はできません
>3、Bは確率4分の1で2回挑戦できるのだから、2分の1になって同じだろう。
一番正論のように見えますが大事なことを一つ忘れています。
「両方当たっても1つしか貰えない」ということです。
この事により一回目の4分の1と2回目の4分の1でかぶるところが発生し純粋に足すことができないということです。
ということは実際には2分の1より少なくなっています。
3番よりAがお得になります。
【問題1−2】
Bコースの確率を簡単に求めます。仮にアとaが当たりだとして
abcd
ア○○○○
イ○×××
ウ○×××
エ○×××
ここの時点では7/16、答えの組み合わせはア〜エとa〜eで16通りですべて確率は一緒。
これらから
Bコースの当たりの確率=7/16*16*1/16=7/16
【問題2】
ここで20000人と言う具体的な数が使われているので使わせてもらいます。
実際に陰性の人(19800人)
正確に診断された人=19800*0.95=18810人(陰性と診断される)
間違って診断された人=990人(陽性と診断される)
実際に陽性の人(200人)
正確に診断された人=200*0.95=190人(要請と診断される)
間違って診断された人=200*0.05=10人(陰性と診断)
これより
陽性と診断された人は1180人でその内本当に陽性の人は190人
よって
190/1180=0.16101694915254237288135593220339
約16.1%
◆神奈川県の高校生 Osamu さんからの解答
【問題1】
賞品をもらえる確率は Aのゲ−ム:1/2
Bのゲ−ム:
最初のゲイムで勝つ事象を C,2回目のゲ−ムで勝つ事象をD とおく。
(求める確率)
=P(C∪D)
=P(C)+P(D)-P(C∩D)
=1/4+1/4-(1/4)2
=7/16
ゆえに、Aのゲ−ム:1/2, Bのゲ−ム:7/16
Aの方が有利。
【問題2】
<<こういう問題って大抵偽>>
検査を受けた20000人のうち、
病気にかかっていないのに陽性と出た人:
(20000[人]-200[人])*(1-95[%])=990[人] ・・・(a)
病気にかかっていないので陰性と出た人:
(20000[人]-200[人])*95[%]=18810[人]
病気にかかっている ので陽性と出た人:
200[人]*95[%]=190[人] ・・・(b)
病気にかかっている のに陰性と出た人:
200[人]*(1-95[%])=10[人]
港さんは(a),(b)のうちの何れかである。
病気にかかっている確率は
190[人]/(990[人]+190[人])=19/118≒16.102...[%]
ゆえに偽。でもちゃんと精密検査すべき。
◆京都府 ゴレンジャイッ!! さんからの解答
【問題[1−1]と[1−2]の解】
Aが当たる確率は1/2
Bのゲームで賞品をもらえる確率は、
1-(2回ともはずれる確率)=1-(3/4)2=7/16 だから、 Aの方が有利といえる。
【問題2】
Aを検査の結果が病気だと示す事象、Cを港さんが病気であるという事象とする。
この場合、Aという条件の下で港さんが病気にかかっている確率P(C/A)は、ベイズの定理より
P(C/A)=P(C)P(A/C)/{P(C)P(A/C)+P(C~)P(A/C~)} ( P(C)+P(C~)=1 )
P(C)=0.01 P(C~)=0.99 P(A/C)=0.95 P(A/C~)=0.05 であるから、
P(C/A)=0.01×0.95/(0.01×0.95+0.99×0.05)=0.161
よって、このとき港さんが病気である確率は約16%であり、港さんの考えは間違いであることがわかる。
・感想
問題1の実験では256回中116回当たって、ほぼ理論通りの結果でした。
問題2は今後のためにもいい問題でした。
◆ 問題へもどる
◆ 今週の問題へ