●,●,●,●,●, ○,○,●,○,○, ●,○,●,●,●, ●,○,●,○,○, ●,●,●,●,●
◆北海道 takuya さんからの解答
【問題1】●,●,●,●,●,
○,○,●,○,○,
●,○,●,●,●,
●,○,●,○,○,
●,●,●,●,●
いわゆる「ナンクロ」に似ていますね。
ExcelのVBAで計算させました。
VBAには2進数にする関数がないので解くのに時間がかかりました。
左上の生徒から順に右方向へ1〜25の番号をつけて解きました。
'10進数⇒2進数
Option Explicit
Dim a As Long '10進数の数値
Dim i As Integer
Dim j As Integer
Dim k As Long
Dim b(1 To 25) As Byte
Dim flag As Boolean
Sub nishinka()
flag = False
Erase b
a = Cells(1, 1).Value
'If a >= 2 ^ 25 Then GoTo errow1
For k = 2 ^ 25 - 1 To 1 Step -1
Erase b
a = k
'******2進化する**********
For i = 1 To 25
If a >= 2 ^ (25 - i) Then
b(i) = 1
a = a - 2 ^ (25 - i)
Else: b(i) = 0
End If
Next
tyousa
If flag = True Then Exit For
Next
If flag = False Then GoTo err1
For j = 1 To 25
Cells(j, 1).Value = b(j)
Next
MsgBox ("解が見つかりました。")
Exit Sub
err1: MsgBox ("解なし")
End Sub
Sub tyousa()
flag = False
Do
If b(2) + b(6) + b(7) <> 1 Then Exit Do
If b(1) + b(3) + b(6) + b(7) + b(8) <> 3 Then Exit Do
If b(2) + b(4) + b(7) + b(8) + b(9) <> 3 Then Exit Do
If b(3) + b(5) + b(8) + b(9) + b(10) <> 3 Then Exit Do
If b(4) + b(9) + b(10) <> 1 Then Exit Do
If b(1) + b(2) + b(7) + b(11) + b(12) <> 3 Then Exit Do
If b(1) + b(2) + b(3) + b(6) + b(8) + b(11) + b(12) + b(13) <> 6 Then Exit Do
If b(2) + b(3) + b(4) + b(7) + b(9) + b(12) + b(13) + b(14) <> 5 Then Exit Do
If b(3) + b(4) + b(5) + b(8) + b(10) + b(13) + b(14) + b(15) <> 7 Then Exit Do
If b(4) + b(5) + b(9) + b(14) + b(15) <> 4 Then Exit Do
If b(6) + b(7) + b(12) + b(16) + b(17) <> 1 Then Exit Do
If b(6) + b(7) + b(8) + b(11) + b(13) + b(16) + b(17) + b(18) <> 5 Then Exit Do
If b(7) + b(8) + b(9) + b(12) + b(14) + b(17) + b(18) + b(19) <> 3 Then Exit Do
If b(8) + b(9) + b(10) + b(13) + b(15) + b(18) + b(19) + b(20) <> 4 Then Exit Do
If b(9) + b(10) + b(14) + b(19) + b(20) <> 1 Then Exit Do
If b(11) + b(12) + b(17) + b(21) + b(22) <> 3 Then Exit Do
If b(11) + b(12) + b(13) + b(16) + b(18) + b(21) + b(22) + b(23) <> 7 Then Exit Do
If b(12) + b(13) + b(14) + b(17) + b(19) + b(22) + b(23) + b(24) <> 5 Then Exit Do
If b(13) + b(14) + b(15) + b(18) + b(20) + b(23) + b(24) + b(25) <> 7 Then Exit Do
If b(14) + b(15) + b(19) + b(24) + b(25) <> 4 Then Exit Do
If b(16) + b(17) + b(22) <> 2 Then Exit Do
If b(16) + b(17) + b(18) + b(21) + b(23) <> 4 Then Exit Do
If b(17) + b(18) + b(19) + b(22) + b(24) <> 3 Then Exit Do
If b(18) + b(19) + b(20) + b(23) + b(25) <> 3 Then Exit Do
If b(19) + b(20) + b(24) <> 1 Then Exit Do
flag = True
Exit Do
Loop
End Sub◆東京都 hirojk さんからの解答
【問題1】●,●,●,●,●,
○,○,●,○,○,
●,○,●,●,●,
●,○,●,○,○,
●,●,●,●,●
<考え方>
生徒の周りには最大で8人居ます。
帽子が7個見えている生徒に注目すると、1つだけ見えている生徒が隣接しています。
その場合、7の生徒が帽子を被っていると、1の生徒の周りは他には帽子を被っていないことになり、もし1の生徒が帽子を被っていても8−2で7の生徒が見える帽子は6こで矛盾します。→7の生徒は帽子を被らない。?,?,?,?,?,
?,?,?,○,?,
?,?,?,?,?,
?,○,?,○,?,
?,?,?,?,?
ここで左下の2の生徒に注目すると、隣り合った3,4の生徒が帽子を絶対に被っていることになります。
左列真中の1は下の3の生徒が帽子を被っているのが確定しているので、周りの他の生徒は帽子を被ってないことになります。?,?,?,?,?,
△,△,?,○,?,
?,△,?,?,?,
●,○,?,○,?,
?,●,?,?,?
左下の7の周りのうち1つ被っていない生徒が決まったので、他の7人は被っていることになります。?,?,?,?,?,
○,○,?,○,?,
▲,○,▲,?,?,
●,○,▲,○,?,
▲,●,▲,?,?
ここで、下行真中の3は決まっていない右側の?が帽子を被っていないと数があいません。
すると一番右下の1は隣の3が被っているので、上の4は帽子を被らないことになります。?,?,?,?,?,
○,○,?,○,?,
●,○,●,?,?,
●,○,●,○,△,
●,●,●,▲,?
右下側の7の周りで帽子を被っていない生徒が分かったので、それ以外は帽子を被っています。?,?,?,?,?,
○,○,?,○,?,
●,○,●,▲,▲,
●,○,●,○,○,
●,●,●,●,▲
右列真中の1は隣が帽子を被っているので、上の一人は帽子を被らないことになります。
すると右上側の7の周りで帽子を被っていない生徒が決まるので、他は帽子を被っています。?,?,▲,▲,▲,
○,○,▲,○,△,
●,○,●,●,●,
●,○,●,○,○,
●,●,●,●,●
あとは左上側の6の生徒、または3の生徒などから残りの二人が帽子を被っているのが分かります。
◆千葉県 なのはな子 さんからの解答
【問題1】●,●,●,●,●,
○,○,●,○,○,
●,○,●,●,●,
●,○,●,○,○,
●,●,●,●,●

[ 図の説明 ]
◆海外 Londonたぬき さんからの解答
【問題1】●,●,●,●,●,
○,○,●,○,○,
●,○,●,●,●,
●,○,●,○,○,
●,●,●,●,●
<考察過程>
少々長いですが。
(縦に上からA、B、C、D、E。横に左からア、イ、ウ、エ、オと番号をふり、例えば上から2つめ、左から3番目の子をB-ウとあらわすことにします。)
(1)B-エは7であることから、この子の周囲8人のうち、帽子をかぶっていない子は1人だけと考えられます。
また、A-オは1人であることから、この2人に共通して見えている、A-エとB-オの子のうち一人は帽子を被っており、もう一方は帽子を被っていないことがわかります。
(何故なら、最初の条件より、A-エとB-オは、「どちらか一方が帽子を被っており、どちらか一方は被っていない」、または「両方とも帽子を被っている」の2通り状態が想定でき、後半の条件より、A-エとB-オは「両方とも帽子を被っている」というケースは否定される為。)
(2)また、同時に、A-オの残りの隣人B-エは帽子を被っていなく、B-エの他の隣人A-ウ、A-オ、B-ウ、C-ウ、C-エ、C-オの6人が帽子を被っていることが確定します。
(3)A-エは3で、(2)から周囲の5人のうち3人の帽子を被っている子(A-ウ、A-オ、B-ウ)が確定していることから、B-オの子が帽子を被っていないことが確定。
この結果、(1)からA-エの子が帽子を被っていることが確定します。
(4)D-エの7、E-オの1に注目して同様の考え方で、D-ウ、E-ウ、B-エ、B-オが帽子を被り、D-エ、D-オが帽子を被っていないことが確定します。
(5)C-ウは3で、これまでにでC-ウの周囲8人のうち帽子を被っている3人(B-ウ、C-エ、D-ウ)が確定したことから、まだ確定していないB-イ、C-イ、C-イの3人が帽子を被っていないことが確定します。
(6)D-イは7で、周囲8人のうち帽子を被っていない子は1人だけ。
且つ、(5)でC-イが帽子を被っていないことが確定していることから、まだ確定していないC-ア、D-ア、E-ア、E-イが帽子を被っていることが確定します。
(7)E-アは2で、帽子を被っている2人(D-ア、E-イ)が確定したことから、D-イは帽子を被っていないことが確定します。
(8)C-アは1で、隣のD-アが帽子を被っていることが確定していることから、確定していないB-アが帽子を被っていないことが確定します。
(9)A-アは1で、周囲の3人のうち2人(B-ア、B-イ)が帽子を被っていないことが確定していることから、残るA-イは帽子を被っていることで確定。
(10)A-イは3で、周囲5人のうちA-ウ、B-ウは帽子を被っており、B-ア、B-イが帽子を被っていないことが各々確定していることから、A-アが帽子を被っていることが確定。
以上で全ての子について確定した。
【問題2−1】
A
<証明>Aの立場で考える。
Aからは、Bが赤で、Cが黒であること、BとC共に手を挙げていることが見えている。
もし、自分が黒であるならば、Bから見えているAとCともに黒帽子となり手を挙げているはずはないから、自分は赤であることが分かる。
(同様の考え方は、Bの立場にたっても成り立つが、AはBよりすばやいという条件から、Aが勝つ。)
尚、CにはAとB共に赤であり、AとB共に手を挙げているのが見える。
Cが赤帽子、黒帽子の場合でもAとBは互いの赤帽子をみて手を挙げている状態が想定できることから、Cは自分が赤か黒か即座には確定出来ない。
【問題2−2】
A (但し、2-1の場合より反応までにしばらく間があり)
A、B、Cは共に他の2人が赤帽子であり、共に手を挙げていることが見えている。
この場合、問題2-1のCの立場に立って考えたとおり、自分の帽子が赤か黒か即座には判定できない。
しかしながら、しばらく後に、Aが聡明ならば。
(以下Aの思考内容)
もし自分(A)が黒帽子ならば、Bからは自分の黒帽子と、Cの赤帽子が見えているはずである。
この時Bは自分(B)が黒帽子と仮定すれば、Cには赤帽子は見えないはずだから、自分の色は黒で無く赤に違いないと判断し、Bは直ぐに自分は赤帽子であると回答するであろう。
同様にCも、自分の帽子が赤帽子であることがすぐ判断できるはずである。
しかしながら、実際にはBもCも即答していないことから、自分は赤帽子であると判断できる。
(B、Cも上記と同様の思考を行い、自分の帽子の色を赤と判断できるが、Aが一番すばやいとの条件から、Aが回答となる。)
【問題2−3】
4すくみ
Aの立場に立って考える。(B,C,Dの立場に立っても同様です。)
Aからは、B、C、Dが共に赤帽子であり、全員手を挙げている状態が見える。
もし、自分(A)が黒、赤どちらの場合であっても、Bは少なくともCとDの2つの赤帽子が見えており、Bは自分が黒帽子であるか、赤帽子であると回答できない。
(何故なら、Bが自分を黒帽子と仮定しても、CとDが赤であることから、CとDがそれぞれ互いの赤帽子を見て手を挙げているのだと推測できる為、Bは自分が赤であると確定出来ない為。)
これは、C、Dについても同じ。
よって自分(A)は、自分が黒か赤か判断出来ない。
◆愛知県 Y.M.Ojisan さんからの解答
問題2−2 はポピュラーですね。
そこでちょっと天邪鬼してみました。
【問題1】
下記のアンダーラインの位置の 7人と1人を手がかりに始めると、下記のとおり。●,●,●,●,●,
○,○,●,○,○,
●,○,●,●,●,
●,○,●,○,○,
●,●,●,●,●
【問題2】
赤を0 黒を1 挙手を1 で状態をあらわします。
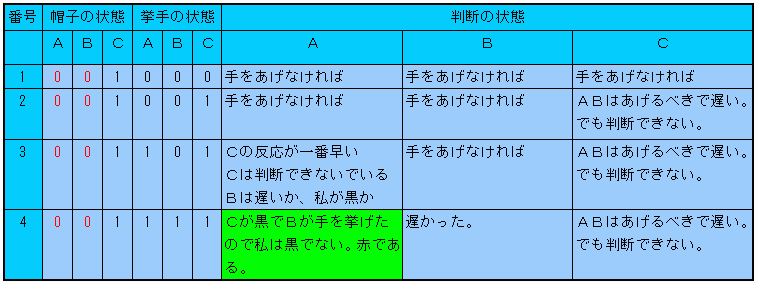
【問題2−1】
Aが勝ち
Cのすばやさは下記のように関係しません。

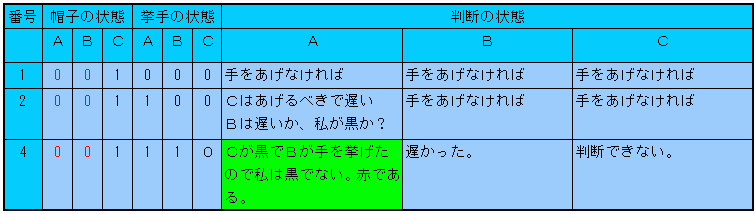
【問題2−2】
Cが勝ち
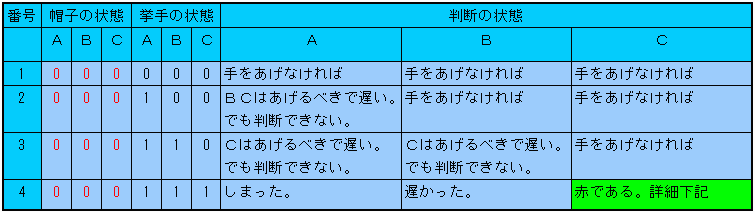
C:自分は一番反応が遅い。
自分が黒であるとすると、自分が挙手した時点で問題2−1の考えた方からAが即座に判断し勝つであろう。
赤の場合は、みんなが判断できない状態にあるので、Aはその状況を確認して自分が赤と確信し、即座に勝つであろう。
よって、ここは赤といってみるしか勝機はない。
【問題2−3】
だれも判断ができない。
自分が赤でも黒でも全員が挙手し、かつ判断出来ない状態であることは矛盾していない。
◆山梨県 Footmark さんからの解答。
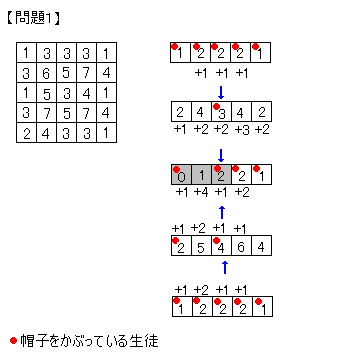
【問題1】
この問題では、
以後、
明らかに帽子をかぶっている生徒を赤マス。
明らかに帽子をかぶっていない生徒を青マス。
どちらか不明な生徒を白マス。
さらに、
帽子をかぶっていない可能性のある生徒を薄青マス。
とします。
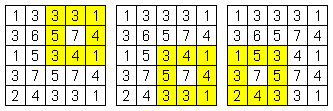
周囲8マスでは、7個が赤マスで1個が青マスの筈です。
そこで、周囲8マスから、それぞれ1個の青マスを探すものとします。
以下、上図の左端の場合を例とします。
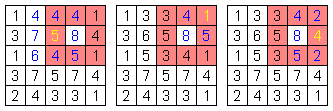
周囲8マスで唯一の青マスを赤マスに変えるものとします。
(上図の黄色数字のマス)
すると、以下になる筈です。
(1) 周囲8マスはすべて赤マス。
(2) 変えたマスを見ることのできる周囲のマスの数字はどれも1つ増える。
(上図の青色数字)
すると(1)より、周囲8マスのどこかのマスに1がそのまま存在するのは明らかに矛盾します。
故に(2)より、1を変えるためには変えたマスは[1のあるマス]からも見えなければなりません。
結局、唯一の青マスは、周囲8マスの内で、[1のあるマス]の周囲のマスであることになります。
すると、それぞれの周囲8マスにおける青マスの各候補は以下の薄青マスとなります。
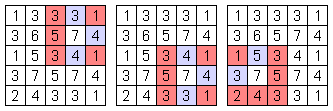
ところで、上の左2つの図では、どちらの図にも[1のあるマス]が2個存在します。
その2個の1を両方とも変えるには、どちらの[1のあるマス]からも見えるマスでなければなりません。
上の右端の図では、[3のある薄青マス]からは既に赤マスが3個見えてます。
ですから、[5のある薄青マス]は赤マスでなく青マスでなければなりません。
すると、それぞれの周囲8マスにおける唯一の青マスは以下と決定します。
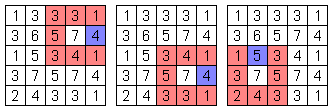
これらを一緒にすると、下の左端の図となります。
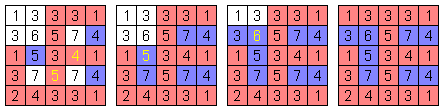
左端の図の黄色数字に注目すると、そのマスから既に数字と等しい個数の赤マスが見えています。
ですから、[7のあるマス]はいずれも青マスです。
(左から2番目の図)
左から2番目の図の黄色数字に注目すると、そのマスから既に数字と等しい個数の赤マスが見えています。
ですから、左上隣の[3のあるマス]や上隣の[6のあるマス]はいずれも青マスです。
(左から3番目の図)
左から3番目の図の黄色数字に注目すると、そのマスから見える赤マスの個数は、マスにある数字より2個不足しています。
ですから、左上隣の[1のあるマス]や上隣の[3のあるマス]の、2個のマスはいずれも赤マスです。
(右端の図)
(余談)
正解が「正解」の頭1文字の「正」の字になっているのが憎いですね。
【問題2】
背理法を使うので、【問題2−1】や【問題2−2】ではAになりきって解答します。
(甲州弁が多少入るかもしれませんが、あしからず。)
【問題2−1】ステージ
おっ、Bが赤でCが黒か。
赤が見えるんだから手も挙げなきゃあ〜。
おうおう、BもCも手を挙げたぞ。
あれ?
俺もCも、Bが赤だから手を挙げたけど、Bは何故手を挙げるんだ?
あっそうか、Cは黒だから俺しかないじゃん。
「は〜い。俺、赤で〜す。」
【問題2−2】ステージ
おっ、今度はBもCも赤だ。
赤が見えるんだから手も挙げなきゃあ〜。
おうおう、BもCも手を挙げたぞ。
まいったなあ、BもCも赤じゃあ俺の色なんて判るわけないじゃん。
俺が何色だって、二人が手を挙げるのに何の不思議もねぇもんなあ〜。
まてよ、もし俺が黒だとすると、【問題2−1】ステージで俺が気付いたようにBもCも気付く筈だぞ。
いくらのろまだって、もう気付いてもいい時間なのに、まだ気付かんぞ。
あっそうか、ちゅうことは俺は黒じゃなくて赤っちゅうこんじゃん。
「は〜い。俺、赤で〜す。」
【問題2−3】
この問題も、自分を仮に黒と仮定すると、他の3人は【問題2−2】ステージのAの立場と一緒です。
ですから、【問題2−2】ステージでAが気付いたように、他の3人もいずれは気付く筈です。
ところが、いくらたっても他の3人が気付かなければ、翻って自分は黒でなく赤と気付くことができます。
[ P・S]
【問題2−2】や【問題2−3】に限らず、3人以上なら同様な背理法が成立します。
でも、気付くまでの時間は人によって、まちまちです。
ですから、どれだけの時間をもって気付かなかったとすべきかが問題です。
また、全員が可能な限りの背理法を駆使することも条件になります。
そんな訳で、現実的には4人以上となると、この推論はあまりあてにならないでしょうね。
◆ 問題へもどる
◆ 今週の問題へ