◆広島県 清川 育男 さんからの解答
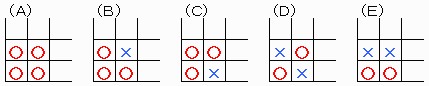
【問題1−1】
後手が有利。
【問題1−2】
先手の手(○または×)と違う(×または○)を点対称となる場所に書く。
(途中で、先手が○から× または ×から○ に変更した場合を含めて。)
ただし、3目となる手があるときは、その手を書く。
【おまけ1】
引き分けに持ち込むことはでない。
問題1−2の必勝法で、○、×の書き方を逆にした場合も勝てるでしょうか。
勝てない。
先手が「後手は先手の点対称の場所に書くと言うことを知っていれば」
先手(5,5)○→後手(6,6)○→先手(7,7)○となり後手は負けてしまう。
【問題2−1】
先手が有利。
【問題2−2】
初手は盤の中心(5,5)に(○または×)を書く。
その後は後手の手と同じマークを点対称の場所に書く。
ただし、3目となる手があるときは、その手を書く。
【おまけ2】
問題2−2の必勝法で、○、×の書き方を逆にした場合も勝てるでしょうか。
勝てない。
後手が「先手は後手の点対称の場所に書くと言うことを知っていれば」
先手(5,5)○→後手(3,3)×→先手(7,7)○→後手(6,6)○→となり先手は負けてしまう。
【問題3】
先手が有利。
中央となる場所に横線を引く。
両狙いで先手必勝となる。
◆東京都 明 さんからの解答
【問題1−1】
後手有利。
【問題1−2】
先手の手に対し、後手は(3連ができるチャンスがくるまで)10×10マスの中心点の点対称の位置に先手とは逆の記号を置く。
もし後手の手順直後に先手が同記号の3連を作る手を打てたとする。
この3連の記号の1つは直前に後手が打ったもの。
(でなければ先手が打った手を先に後手が打って後手勝ち)
上記の後手の打ち方のルールによれば直前に後手が打った形が中心点の点対称の位置に(記号を逆にして)存在する。
したがって後手は直前に打った手の替わりに、先手が3連を作った手の点対称の位置に逆の記号を打てば3連を作れる。
よって上記ルールによれば後手は負けることはない。
【おまけ1】
引き分けに持ち込めないことが以下のとおり証明される。
引き分けに持ち込めたとして、マスが全部○×でうめられたとする。
この埋められたパターンの中に、2行〜9行かつ2列〜9列の範囲に次のパターンは存在してはいけないことを以下に示す。
○○
×× (90°回転、○×逆は同型)
引き分けであればこのパターンの中でどれか1つの記号が最後に打たれる。
この位置を□で表す。
○○
×□(□がどの位置でも以下の議論は同じ)
上記パターンが存在する中で勝負がつかないのためには、このパターンの回りを含む記号の配置は以下のようになっていなければならない。×○○×
×□
○
すなわち□の位置に○を置けば3連を作れる。
これは引き分けに持ち込めるとしたことに矛盾する。
したがって引き分けに持ち込むためには上記パターンが存在してはならない。
(2行〜9行かつ2列〜9列の範囲で)
ところが中心点の周りの4つのマスには後手が【問題1−2】のルールを取る限り、上記パターンが必ず発生する。
以上によりこの勝負は引き分けに持ち込むことはできない。
(後手必勝)
○、×の書き方を逆にした場合も勝てるでしょうか。?
後手が先手の逆の記号を打たないと言う意味であれば先手勝ち。
【問題2−1】
先手有利
【問題2−2】
まず先手は中心(5行、5列)のマスに○または×を置く。
以下、先手は後手が打つ手に対し、(3連ができるチャンスがくるまで)上記中心のマスに対し対称な位置に後手が打った記号と同じ記号を打つ。
【問題1−2】と同様議論で先手が負けないことを証明できる。
また負けないためには中心マスの回りのマスには中心マスと逆の記号を置いていかなければならないことからこの中で3連が発生することになる。
したがって先手必勝。
【おまけ2】
○、×の書き方を逆にした場合も勝てるでしょうか。?
先手が後手と同じ記号を打たないと言う意味であれば後手勝ち。
【問題3】
先手有利かつ必勝
後手に必勝の戦略があるすれば、先手が適当な位置に線を入れた後、後手が取る手に対し、先手が同様の戦略をとれば先手が勝てることになる。 → 矛盾
先に先手が始めに入れた線は後の先手の手を邪魔することはない。
(先手がその位置に線を入れる必要があれば、すでに線が入れられているのであるから別の位置に、例えば一番上の2点間を無意味につないでおけばよい)
したがって先手有利。
赤と青がつなげられるすべての線をつなぎ終わったとして、青が左右に線をつなげなかったとすれば、青の線で連結された左のグループと右のグループに分かれる。
この2つのグループの間は赤の線が通る隙間ができるため、赤の線が上下につなげられる。
したがって、引き分けはなく、先手必勝。
トライアンドエラーでそうらしいと見えても、証明しようとするとむずかしいですね。
◆愛知県 Y.M.Ojisan さんからの解答
【問題1−1】
後手が有利
【問題1−2】
先手の打った手に対し反対の手を打つか、勝負が決まる手を必ず打つ。
ここで反対とは マークを○なら×、×なら○
打つ位置を恒に点対称位置 か 恒に鏡像対称位置とする。
【おまけ1】
(1)引き分けには持ち込めない。
(2)○×を逆にすると負ける。
(1)∵

上図に示す隅の全ての状態から始めて、引き分けになるための必然の状態を詰めてゆくと、詳細は省略するが、基本的に同じ構造の下図の2タイプだけが引き分けの最終状態である。
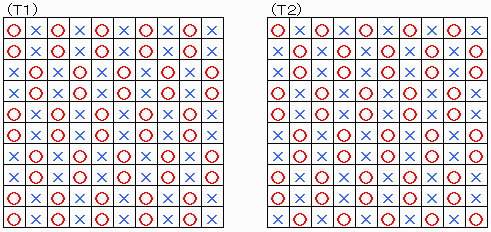
背理法により証明する。
(T1)または(T2)の状態で終了する手順があったとする。
すると、いずれも下図(P1)のような部分を含んでいる。
引き分けであるので、黄色の枠部分もいずれ全て手を入れなければならないが、緑の枠があいている状態で、黄色を埋めると空きの緑に打って勝負がついてしまう。
従って引き分けであるためには、緑色枠は黄色枠が埋まる前に埋まっていなければならない。
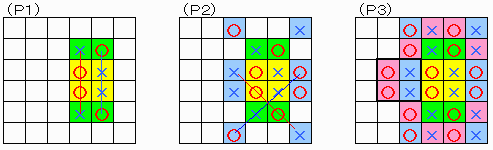
さらに、(P1)の状態になる前には上手(P2)の青枠の部分が埋まっていなければならない。
同様にその前に(P3)の桃色枠も埋まっていなければならない。
ここで(P3)の図において太枠で囲まれた2×2の枠を考えると、これを黄色枠と置き換えてもよく、同じことが言える。
つまり黄色枠内は太線枠内より先に埋まっている必要がある。
これは矛盾である。
よって、引き分けはなく、後手が有利なので、後手必勝である。
(2)∵たとえば下図 黄色枠が先手、緑枠が後手を示している。
先手が勝っている。黒点はボードの中心。太線はボード中央の線。
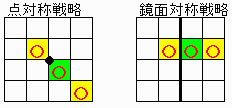
【問題3】
先手が有利である。
∵このゲームは引き分けが無い。
なぜなら、もし引き分けがあるとすると、どちらも相手の線の連なりで分断されなければならないが、その場合は線の連なりが交差するしかないのでルールに反する。
従って、先手は、縦に繋がることを目標にしつつも、後手の封鎖だけを考えて手を打って行けば、自然に勝てる。
封鎖の基本形は図1の3本の赤2重線である。
先手(赤)1手目は図1の一列一行目の縦線を打つ。
これにより左列の青点のうち1行目のものが完全に封鎖される。
残りの三個の青点から出る枝は、赤2重線により分断され、必ず伸びる方向が1方向に限られる局面があり、そこからは先は下図紫の線で示されるように、先手により、封鎖されるか上に伸びるしかなくなるようにされるだけであり、右側へは進めず後手は勝てない。
図1−2のように、後手が4行目で伸びたとしても、先手は図示のように先手の4手目で封鎖可能である。
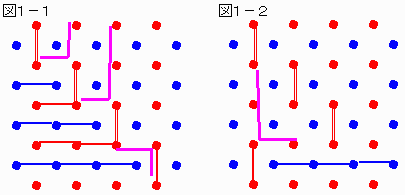
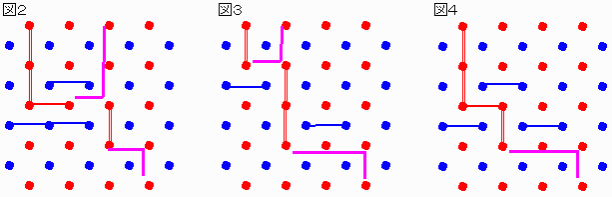
後手は図1の状態ならないように抵抗できるが、それらは図2〜4の何れかのパターンに先手はすることができ、これらは伸びる枝が2本か1本になるので、図1より封鎖しやすい状態である。
◆ 問題へもどる
◆ 今週の問題へ