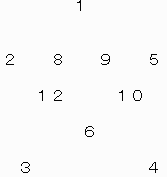
◆神奈川県の小学生 ☆KANA☆ さんからの解答
【問題1】赤● 緑◆ 黄■ 青★
黄◆ 青● 赤★ 緑■
青■ 黄★ 緑● 赤◆
緑★ 赤■ 青◆ 黄●
【問題2】
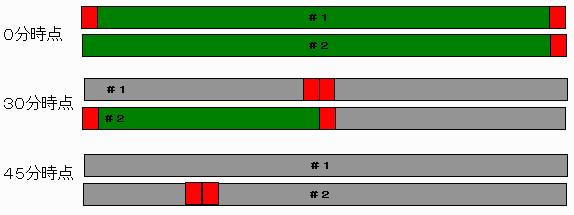
まず、2つの蚊取り線香のうち1つは両はじから、もう1つは片側だけから、同時に火をつける。
すると、30分後に、両はじから火をつけたほうが燃え尽きる。
片側だけから火をつけたほうは、ちょうど半分のところまで燃えている。
その時に、はじめ片側だけから火をつけた方の蚊取り線香のもう片方のはじから火をつける。
すると、15分後にそちらの蚊取り線香も燃え尽きる。
始めの30分とあわせて、45分後に、ちょうど二つの蚊取り線香が燃え尽きたことになる。
◆上海日本人学校2年生 中山晨超 さんからの解答
【問題1】
【原始的な考え方(笑)】
僕は消去法で解きました。
まず、赤●,青◆,緑★,黄■をベースとして考えます。
(どこかの列、行、斜めに必ず「赤●,青◆,緑★,黄■」の組み合わせがあるはずです。)
それで、赤●,青◆,緑★,黄■を下のように置きます。
(どこでも良いのですが、斜めに置いたほうが少し簡単になります) 1 2 3 4
1赤●,**,**,**,
2**,青◆,**,**,
3**,**,緑★,**,
4**,**,**,黄■
例えば(1、2)を考えてみます。
ここには、1の列には赤,●、2の行には青,◆が使われているので、黄★か緑■しか置けない事になります。
※緑★、黄■はもう使われている
つまり、もうここで選択肢が二つになったわけです。
<黄★の場合>
まず黄★を置きましょう。 1 2 3 4
1赤●,**,**,**,
2黄★,青◆,**,**,
3**,**,緑★,**,
4**,**,**,黄■
すると、(1、3)は青■に確定されます。
次に、(1、4)は緑◆に確定されます。
このように、確定されるところにどんどん駒を置いていけば、いずれ全てのマスに駒が置かれ、問題1が解けます。
しかし、この選択肢の場合、置けなくなる(矛盾が起こる)時がきます。
つまり、この選択肢は誤ってたという事になるので、残りの緑■が正解に導く選択肢になります。
そうして、出てきた答えがこれです。
【答え】赤●,黄★,青■,緑◆,
緑■,青◆,黄●,赤★,
黄◆,赤■,緑★,青●,
青★,緑●,赤◆,黄■
【問題2】
蚊取り線香をA、もう一方の蚊取り線香をBとする。
最初にAのはじめの方ととおわりの方の両方に火をつける。
Bははじめの方だけに火をつける。
Aがすべて燃え尽きたら、(その時は1時間の1/2なので30分間経過した事になる)Bの終わりの方に火をつける。
(現時点Bは30分が過ぎたので、残り30分間の蚊取り線香が残っている事になる)
そしてBがすべて燃え尽きる。
(その時は30分の1/2なので終わりの方につけてから15分経過した事になる)
結論:
AとBに火をつけた時からBが燃え尽きた時間は45分間である。
感想;単純なんだけど、実用的で興味深い問題ですね。
◆広島県 清川 育男 さんからの解答
【問題1】変形ラテン方陣ですね。赤●,青◆,緑★,黄■,
緑◆,黄●,赤■,青★,
黄★,緑■,青●,赤◆,
青■,赤★,黄◆,緑●
【問題2】
2本の香取線香をA,Bとする。
1)
同時に、
Aの香取線香は両端に点火する。
Bの香取線香は1方の端に点火する。
2)
Aの香取線香が燃え尽きたときに、Bの香取線香のもう1方の端に点火する。
3)Bの香取線香が燃え尽きたときが、45分。
60÷2+30÷2=45
【問題3】
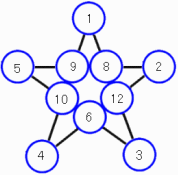
1+8+12+3=24
3+6+10+5=24
5+9+ 8+2=24
2+12+6+4=24
4+10+9+1=24
【おまけ】

A+F+G+C=24
C+H+I+E=24
E+J+F+B=24
B+G+H+D=24
D+I+J+A=24
2*(A+B+C+D+E+F+G+H+I+J)=120
A+B+C+D+E+F+G+H+I+J=60
A,B,C,D,E,F,G,H,I,J はすべて異なる自然数であり、
1+2+3+4+5+6+7+8+9=45 であるから、最大の数は15以下でなければならない。
したがって、A,B,C,D,E,F,G,H,I,J はすべて15以下の数でなければならない。
結果的に、11,14,15は使えない。
これは、プログラムで探索した結果ですが、数学的な証明は保留。
上図を固定しての結果(プログラムによるの探索。)240通り。
上図を固定しない場合(回転、裏返し。)
240÷10=24
24通り。
2つのグループに分かれることに気づきました。
1) (1,2,3,4,5,6,8,9,10,12) 10個
2) (1,2,3,4,5,6,7,9,10,13) 10個
結果は同数組。
これで、数学的に証明すべきことが揃ったと思います。
◆愛知県 Y.M.Ojisan さんからの解答
【問題1】
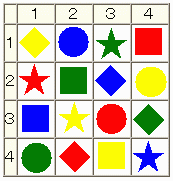
(蛇足)
本問題は魔方陣を2段のラテン方陣からつくる問題と近い。
下図は解答に対応する4方陣である。
従って解答は対角線上もばらばらになっている。
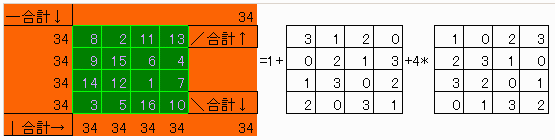
【問題2】 下図手順
【問題3】
【おまけ】
(1)すべて2回ずつ使用されており、
全合計×2=5×24より 全合計=60である。
(2)1点Pをとおる2方向の和を考えると
2P+その他6点合計=2×24 である。
その他合計の最小値は1+2〜6=21であるので P=13が最大である。
(3) 1を使わないと2〜11の和は65で60を超過する。
よって1は必須。同様に1〜5は必須。
即ち1〜5の5個と 6〜13から選んだ異なる数字5個の合計が60であるものを使用しなければならない。
よって1〜5 以外の数字の組み合わせは
(6,7,8,11,13) (6.,7,9,10,13) (6,7,9,11,12)
(6,8,9,10,12) (7,8,9,10,11)の5通りである。
(4)l回転対称、左右対称に加え、下図のような内外入れ替えの対称性がある。
よって、回転対称(5対称)と内外入れ替え(2対称)を使って、
左図でのA1=1に限定(10対称)してよい。
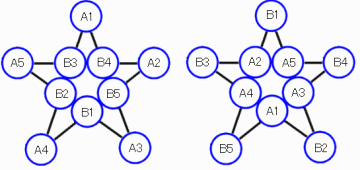
さらに、B1≠2の場合、左右対称性で
2の入れ場所は→A2|A3|B2|B3 のみを考えればよい。
一方、B1=2の場合は左右対称性で
3の入れ場所は→A2|A3|B2|B3 を考えればよい。
(5)A1〜A5が決まると B1〜B5は下記で計算される。
B[i]=12+A[i]-A[i-1]-A[i+1]
添え字iは1〜5。
添え字加減結果は mod(結果-1,5)+1を行う。
以上を用いて限定的に探索すると、全部で12通りあった。
従って実際にはその20倍の240とおりである。
下記は 探索結果を A=[A1 A2 A3 A4 A5]、 B=[B1 B2 B3 B4 B5] で表記したものである。
さらに対称性があり基本形を削減できるようである。A=[ 1 2 3 4 5] B=[ 6 10 9 8 12]
A=[ 1 2 3 9 6] B=[ 5 10 4 12 8]
A=[ 1 2 10 8 6] B=[ 5 3 12 4 9]
A=[ 1 2 10 12 5] B=[ 6 3 8 9 4]
A=[ 1 2 3 4 6] B=[ 5 10 9 7 13]
A=[ 1 2 3 9 5] B=[ 6 10 4 13 7]
A=[ 1 2 10 7 5] B=[ 6 3 13 4 9]
A=[ 1 2 10 13 6] B=[ 5 3 7 9 4]
A=[ 1 5 9 13 6] B=[ 2 7 3 10 4]
A=[ 1 6 4 7 5] B=[ 2 13 3 10 9]
A=[ 1 6 9 12 5] B=[ 2 8 3 10 4]
A=[ 1 5 4 8 6] B=[ 2 12 3 10 9]
◆ 問題へもどる
◆ 今週の問題へ