『今週の問題』第147回　解答

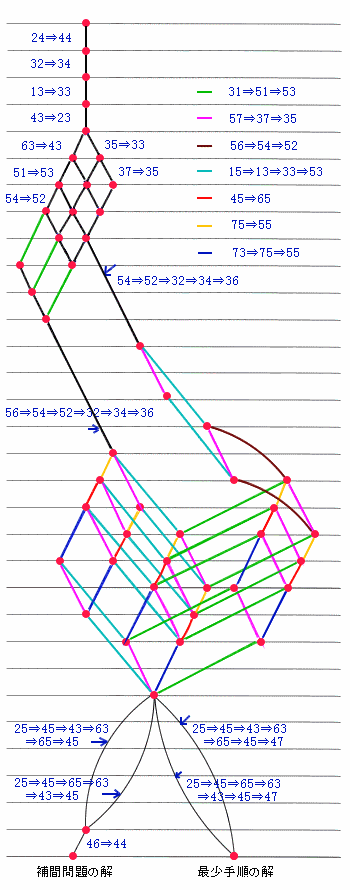
◆千葉県　なのはな子 さんからの解答

【問題１】

［A］
(4,6)→(4,4)，(2,5)→(4,5)，(3,7)→(3,5)，(4,5)→(2,5)，(1,5)→(3,5)，
(3,4)→(3,6)，(5,7)→(3,7)，(3,7)→(3,5)，(6,5)→(4,5)，(4,5)→(2,5)，
(1,3)→(1,5)，(1,5)→(3,5)，(5,3)→(5,5)，(5,6)→(5,4)，(7,3)→(5,3)，
(4,3)→(6,3)，(7,5)→(7,3)，(7,3)→(5,3)，(5,3)→(5,5)，(5,1)→(5,3)，
(2,3)→(4,3)，(4,3)→(6,3)，(6,3)→(6,5)，(6,5)→(4,5)，(4,5)→(2,5)，
(2,5)→(2,3)，(4,1)→(4,3)，(4,4)→(4,2)，(3,1)→(3,3)，(2,3)→(4,3)，
(4,3)→(4,1)

［B］
(4,6)→(4,4)，(6,5)→(4,5)，(4,4)→(4,6)，(5,7)→(5,5)，(2,5)→(4,5)，
(4,5)→(6,5)，(7,5)→(5,5)，(3,7)→(3,5)，(4,7)→(4,5)，(4,5)→(2,5)，
(1,5)→(3,5)，(6,3)→(6,5)，(6,5)→(4,5)，(4,5)→(2,5)，(2,4)→(4,4)，
(4,4)→(6,4)，(4,3)→(6,3)，(7,3)→(5,3)，(3,2)→(3,4)，(1,3)→(1,5)，
(1,5)→(3,5)，(3,5)→(3,3)，(2,3)→(4,3)，(4,3)→(6,3)，(5,1)→(5,3)，
(7,4)→(5,4)，(5,4)→(5,2)，(3,1)→(5,1)，(5,1)→(5,3)，(6,3)→(4,3)，
(4,3)→(4,1)

［C］
(4,6)→(4,4)，(2,5)→(4,5)，(3,7)→(3,5)，(4,5)→(2,5)，(1,5)→(3,5)，
(6,5)→(4,5)，(4,5)→(2,5)，(1,3)→(1,5)，(1,5)→(3,5)，(3,4)→(3,6)，
(5,7)→(3,7)，(3,7)→(3,5)，(5,3)→(5,5)，(5,6)→(5,4)，(7,3)→(5,3)，
(5,3)→(5,5)，(5,1)→(5,3)，(4,3)→(6,3)，(7,5)→(7,3)，(7,3)→(5,3)，
(4,1)→(4,3)，(4,3)→(6,3)，(6,3)→(6,5)，(6,5)→(4,5)，(4,5)→(2,5)，
(2,3)→(4,3)，(3,1)→(3,3)，(4,4)→(4,2)，(2,5)→(2,3)，(2,3)→(4,3)，
(4,3)→(4,1)

［A］  21手
(4,6)→(4,4)，(2,5)→(4,5)，(3,7)→(3,5)，(4,5)→(2,5)，(1,5)→(3,5)，
(3,4)→(3,6)，(5,7)→(3,7)，(3,7)→(3,5)，(6,5)→(4,5)，(4,5)→(2,5)，
(1,3)→(1,5)，(1,5)→(3,5)，(5,3)→(5,5)，(5,6)→(5,4)，(7,3)→(5,3)，
(4,3)→(6,3)，(7,5)→(7,3)，(7,3)→(5,3)，(5,3)→(5,5)，(5,1)→(5,3)，
(2,3)→(4,3)，(4,3)→(6,3)，(6,3)→(6,5)，(6,5)→(4,5)，(4,5)→(2,5)，
(2,5)→(2,3)，(4,1)→(4,3)，(4,4)→(4,2)，(3,1)→(3,3)，(2,3)→(4,3)，
(4,2)→(4,4)

［B］   21手
(4,6)→(4,4)，(6,5)→(4,5)，(4,4)→(4,6)，(5,7)→(5,5)，(2,5)→(4,5)，
(4,5)→(6,5)，(7,5)→(5,5)，(3,7)→(3,5)，(4,7)→(4,5)，(4,5)→(2,5)，
(1,5)→(3,5)，(6,3)→(6,5)，(6,5)→(4,5)，(4,5)→(2,5)，(2,4)→(4,4)，
(4,4)→(6,4)，(4,3)→(6,3)，(7,3)→(5,3)，(3,2)→(3,4)，(1,3)→(1,5)，
(1,5)→(3,5)，(3,5)→(3,3)，(2,3)→(4,3)，(4,3)→(6,3)，(5,1)→(5,3)，
(7,4)→(5,4)，(5,4)→(5,2)，(3,1)→(5,1)，(5,1)→(5,3)，(6,3)→(4,3)，
(4,2)→(4,4)

［C］  21手
(4,6)→(4,4)，(2,5)→(4,5)，(3,7)→(3,5)，(4,5)→(2,5)，(1,5)→(3,5)，
(6,5)→(4,5)，(4,5)→(2,5)，(1,3)→(1,5)，(1,5)→(3,5)，(3,4)→(3,6)，
(5,7)→(3,7)，(3,7)→(3,5)，(5,3)→(5,5)，(5,6)→(5,4)，(7,3)→(5,3)，
(5,3)→(5,5)，(5,1)→(5,3)，(4,3)→(6,3)，(7,5)→(7,3)，(7,3)→(5,3)，
(4,1)→(4,3)，(4,3)→(6,3)，(6,3)→(6,5)，(6,5)→(4,5)，(4,5)→(2,5)，
(2,3)→(4,3)，(3,1)→(3,3)，(4,4)→(4,2)，(2,5)→(2,3)，(2,3)→(4,3)，
(4,2)→(4,4)

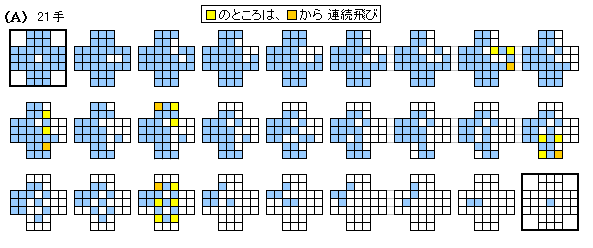
【コメント】

実は最短は１８手なのですが、とてもわかりやすく示してくださったので紹介します。

◆宮城県　アンパンマン さんからの解答

【問題１】

(2,4)→(4,4)，(3,2)→(3,4)，(1,3)→(3,3)，(1,5)→(1,3)，(4,3)→(2,3)，
(1,3)→(3,3)，(3,4)→(3,2)，(3,1)→(3,3)，(3,6)→(3,4)，(5,5)→(3,5)，
(2,5)→(4,5)，(5,7)→(5,5)，(5,5)→(3,5)，(4,7)→(4,5)，(3,4)→(3,6)，
(3,7)→(3,5)，(6,3)→(4,3)，(5,1)→(5,3)，(4,3)→(6,3)，(4,1)→(4,3)，
(7,3)→(5,3)，(7,5)→(7,3)，(4,3)→(6,3)，(7,3)→(5,3)，(3,5)→(5,5)，
(6,5)→(4,5)，(5,4)→(5,2)，(4,5)→(4,3)，(3,3)→(5,3)，(5,2)→(5,4)，
(6,4)→(4,4)

　　ＡＢＣ
　　ＣＡＢ
ＣＡＢＣＡＢＣ
ＢＣＡＢＣＡＢ
ＡＢＣＡＢＣＡ
　　ＢＣＡ
　　ＡＢＣ

N(A),N(B),N(C)＝Ａ，Ｂ，Ｃのマス目にある石の数。

石が飛ぶごとに N(A),N(B),N(C)は奇数の場合は偶数に変わり、また偶数の場合は奇数に変わります。

そのため問題１）の場合は
（N(A),N(B),N(C)）＝（１１，１０，１１）から始まる場合、
（N(A),N(B),N(C)）＝（０，１，０）で終わることができますが、
（１，０，０）や（０，０，１）で終わることができません。

つまり最後の位置はＢにならなければなりません。

Ａ、Ｃから石一個取り除く場合も最後の位置はＡ，Ｃになることが言えます。

そのため、どのマス目から石を取り除いても最後の石はそのマス目にすることが極めて高い確率でできます。
すべてのマス目ができることを証明するために、手順を示す必要があります。

（予想）

どのマス目を取り除いても、最後の位置はそのマス目にすることができます。

◆東京都　未菜実 さんからの解答

Peg Solitaire　の全解答をグラフ化したのを見つけました。
http://ch.twi.tudelft.nl/~sidney/puzzles/に載っていました。

【おまけ２】

「数理パズル」(中公新書)にあります。

図１の様にABCを振ります。

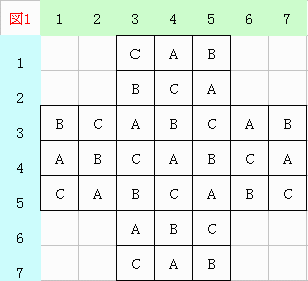
例えば、中央44が空白の場合を考えると、Aは10個、Bは11個、Cは11個です。
つまり偶数、奇数、奇数になっています。

そして跳ぶ度に、偶奇奇⇒奇偶偶⇒偶奇奇⇒奇偶偶と繰り返す事になります。

ですから、最後に一つ残るとすればAの升目でないといけない事になります。
（B、C は同時に偶数であるか奇数であるかです。）

図 1 には左右ひっくり返した図が存在しますので、そのことも考慮する必要があります。
これによって各升目の性質が特定された事になります。

図１とそれを組み合わせたのが、図２で、各文字、例えば AA から出発するとAA で終わる事になります。
(上下方向に考えても同じ図になります。)

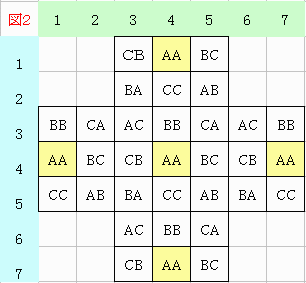
と言う事で解答が存在すれば、その最後の位置が図２で示されたわけです。

　◆ 問題へもどる

　◆ 今週の問題へ

数学の部屋へもどる