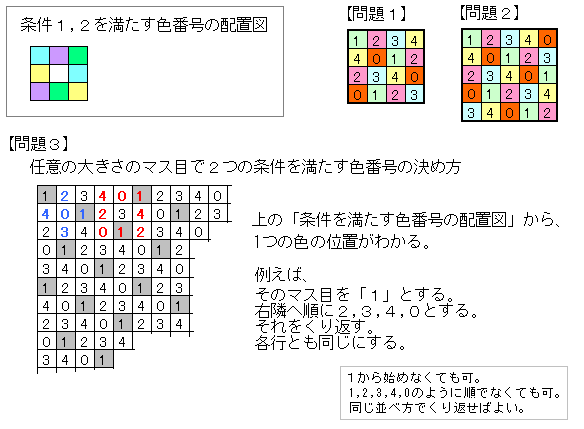
���_�ސ쌧�@���� ����̉�
�y���P�z3�C4�C0�C1�C
0�C1�C2�C3�C
2�C3�C4�C0�C
4�C0�C1�C2
�y���Q�z3�C4�C0�C1�C2�C
0�C1�C2�C3�C4�C
2�C3�C4�C0�C1�C
4�C0�C1�C2�C3�C
1�C2�C3�C4�C0
�y���R�z
�^�C����s[0],s[1],s[2],s[3],s[4]�ƕ\���B
(s[0]�`s[4]��0�C1�C2�C3�C4�̂��ꂼ��قȂ鐔�łǂ�ȏ��Ԃł��j
�^�C���̍ŏ��̍s��
s[0]s[1]s[2]s[3]s[4]s[0]s[1]s[2]s[3]s[4]s[0]s[1]s[2]...��n���ׂ�B
����ɑ����s�͏�̃^�C������^�C���Q�����ɂ��炵�ĕ��ׂ�B
2�s�ځ@s[2]s[3]s[4]s[0]s[1]s[2]s[3]s[4]s[0]...
3�s�ځ@s[4]s[0]s[1]s[2]s[3]s[4]s[0]s[1]s[2]...
�ȉ��An�s�ڂ܂ł�����J��Ԃ��B
���̂Ƃ��A
a�s1��ڂ̃^�C���́@s[mod(2(a-1),5)]
a�sb��ڂ̃^�C����s[mod[(mod[2(a-1),5]+mod[b-1,5]),5]
�ŕ\�����B
���R�����@Footmark ����̉�
�y���P�z�O�P�Q�R
�R�S�O�P
�P�Q�R�S
�S�O�P�Q
�y���Q�z�O�P�Q�R�S
�R�S�O�P�Q
�P�Q�R�S�O
�S�O�P�Q�R
�Q�R�S�O�P
�y���R�z
�F�̌��ߕ��͎��̂Q�ʂ�̂ǂ��炩���ȒP�B
���{�錧�@�A���p���}�� ����̉�
�y���P�z2�C0�C3�C1�C
1�C4�C2�C0�C
0�C3�C1�C4�C
4�C2�C0�C3
�y���Q�z1�C2�C3�C4�C0�C
4�C0�C1�C2�C3�C
2�C3�C4�C0�C1�C
0�C1�C2�C3�C4�C
3�C4�C0�C1�C2
�y���R�z
X(i,j)��(i,j)�̃}�X�ڂ̐F�Ƃ����
X(i,j) ��2a-b (mod 5) �܂��� X(i,j) ��2b-a (mod 5)
�F�Ɛ����̃}�b�s���O���l�����
�h����@����2*(5!)=240���@�@(a,b���\���傫���Ƃ��j
����t���@�Ȃ̂͂Ȏq ����̉�

�������s�@�ʂ肷���� ����̉�
�y���P�z1�C2�C3�C4�C
3�C4�C0�C1�C
0�C1�C2�C3�C
2�C3�C4�C0
����̐F�����ւ������̂ƁA�����̋����i���Ԃ������́j�B
�y���Q�z1�C2�C3�C4�C0�C
4�C0�C1�C2�C3�C
2�C3�C4�C0�C1�C
0�C1�C2�C3�C4�C
3�C4�C0�C1�C2
����̐F�����ւ������̂ƁA�����̋����i���Ԃ������́j�B
�y���R�z
(i,j)���W�̃}�X�̐F��c(i,j)(=0,1,2,3,4)�Ƃ���ƁA
a,b��4�̎��A
c(i,j) = (i+2j) % 5
((i+2j)��5�Ŋ������]��B0��i��a, 0��j��b) ---(1)
�܂��́A
c(i,j) = (i+3j) % 5
(0��i��a, 0��j��b) ---(2)
�i(2)��(1)�̋����i���Ԃ������́j�j
�ł���B
�y�ؖ��z
�S�~�S�}�X�̏ꍇ�Ɏ����A������傫���}�X�̏ꍇ�́A���̒��̔C�ӂ̂S�~�S�}�X�ɂ��� �l����A�ȒP�ɂ킩��B
�����P�C�Q���A���̏����R���킩��B
�����R�F���̐}�ŁA11�̐F�͑���00�`22�̐F�Ƃ͈قȂ�B00, 10, 20,
01, 11, 12,
20, 21, 22
�S�~�S�}�X�̏ꍇ�A00, 10, 20, 30,
01, 11, 12, 31,
20, 21, 22, 32,
30, 31, 32, 33
��̐}�ŁA11�𒆐S�ɏ����P�C�Q���A12�𒆐S�ɏ����R��K�p����ƁA
c(1,2)=c(0,0) �܂��́Ac(2,0)
�܂����l�ɁA22�𒆐S�ɏ����P�C�Q��K�p����ƁA
c(1,2)=c(3,1) �܂��́Ac(3,3)�@�ƂȂ�B
c(1,2)=c(2,0)=c(3,1)�Ƃ���ƁA21�𒆐S�ɏ����Q�ɖ����B
c(1,2)=c(0,0)=c(3,3)�Ƃ���ƁA22�ɏ�Ɠ��l�̂��Ƃ��l����ƁA
c(2,1)��c(1,2)���Ac(2,1)=c(2,0)=c(3,1)�ƂȂ薵���B
����āA
c(1,2)=c(0,0)=c(3,1) ---(1*)
�܂��́A
c(1,2)=c(2,0)=c(3,3) ---(2*)
�ƂȂ�B
�S�̂��X�O�x���Ƃɉ�]�������̂��l���邱�ƂŁA
(1*)�̏ꍇ�A(1)�A(2*)�̏ꍇ�A(2)�ƂȂ�B
�������s�@�F�t ����̉�
��ʉ����������܂��B
M * N �̒����`�ɌܐF�̐F��h�蕪����B
���̐F���A0, 1, 2, 3, 4 �ŕ\���B
�܂��A(i, j) �̈ʒu�̐F���Ac(i, j) �ŕ\���B
���̂悤�ɍċA�I�ɐF���`����B
c(0, 0) = 0
c(i, j+1) = c(i, j) + 2 mod 5
c(i+1, j) = c(i, j) + 1 mod 5
���̂Ƃ��A�C�ӂ� 3 * 3 �̐����`�ŁA���������Ă��邱�Ƃ������Ηǂ��B
c(i, j) = 0 �Ƃ��Ă��ȉ��͈�ʐ�������Ȃ��B
| (i, j) | (i, j+1) | (i, j+2) | 0 | 2 | 4 | |
| (i+1,j) | (i+1,j+1) | (i+2,j+1) | c===> | 1 | 3 | 0 |
| (i+2,j) | (i+2,j+1) | (i+2,j+2) | 2 | 4 | 1 |
�����m���@Y.M.Ojisan ����̉�
�y���P�A�Q�z
 �@
�@
�y���R�z
�F�ԍ���a+2*b mod �T
����т��̐F�����┽�]�������́B
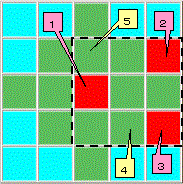
�扺�}[1]�̘g�𒆐S����ђ[�Ƃ��ď����P��K�p����ƁA���}�u�v�̘g��[1]�Ɠ����F�ɂł��Ȃ��B
�]���āA�����Q�̂��߂ɂ͉��}�j�����̂R�~�R�g�̂����A[2]��[3]�̈����[1]�Ɠ����F�ł���
����[2]�ł���Ƃ���B[3]�͏㉺���]�őΏ̂ɂȂ�B
���l�ɔj���g����[4]�ɂ�[2]��[5]���Ή����A[2]���g���Ȃ��̂�[5]��[4]�͓����F�łȂ���Ȃ�Ȃ��B
�ȏ���J��Ԃ��Δj���g���̐F�z�u�����肷��B
���̔j���g�𒆐S�Ɏ��ӂ̂R�~�R�g�͓��l�ɂ��Ĉ�ӂɌ��܂�I���̗]�n�͖����B
����ĐF�z�u�͖��P�A�Q�̂悤�Ȉ������̌j�n��єz�u�݂̂ł���B
�������s�@You.O ����̉�
�悁�s����̃}�X�ڂ�(a,b)�ŕ\���A���̃}�X�ڂ̐F�ԍ����b(a,b)�ŕ\�����Ƃɂ���B
�y���P�z
�^����ꂽ�����P�ɂ��A�T�̃}�X��
(1,2)�C(2,1)�C(2,2)�C(2,3)�C(3,2)�̐F�͂��ׂĈقȂ�̂ŁA�����̃}�X�ڂ̐F�ԍ������ꂼ��A
�b(1,2)=�O�C�b(2,1)=�P�C�b(2,2)=�Q�C�b(2,3)=�R�C�b(3,2)=�S�Ƃ���B
���̂Ƃ������Q�ɂ��A�S�̃}�X��
(1,1)�C(1,3)�C(3,1)�C(3,3)�̐F�ԍ��̑g�ݍ��킹�́A
�i�b(1,1)�C�b(1,3)�C�b(3,1)�C�b(3,3)�j��(3�C4�C0�C1�j�C�i4�C1�C3�C0�j�̂Q�ʂ肵���Ȃ��B
���̑g�ݍ��킹�����߂Ă��܂��ƁA�����P����я����Q�ɂ���Ďc��̃}�X�ڂ̐F�͎����I�Ɂi��ӂɁj���肳���B
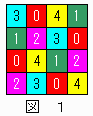
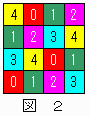
�����̏ꍇ�ɂ��āA�S�s�~�S�ׂẴ}�X�ڂ̐F�̓h�����}�P����ѐ}�Q�Ɏ����B
 �@
�@
���ۂɂ́A�T�̃}�X��(1,2)�C(2,1)�C(2,2)�C(2,3)�C(3,2)�̐F�̌��ߕ���
�T�I���P�Q�O�i�ʂ�j����A���̊e�X�ɑ��ĂS�̃}�X��
(1,1)�C(1,3)�C(3,1)�C(3,3)�̐F�̌��ߕ����Q�ʂ肸���邩��A
����̂R�s�~�R��̃}�X�ڂɂ��āA���̐F�̌��ߕ���
�P�Q�O�~�Q���Q�S�O�i�ʂ�j�ƂȂ�B
���̂X�̃}�X�ڂ̐F�����肷��ƁA�c��̃}�X�ڂ̐F�͈�ӓI�ɒ�܂邩��A�F�̓h����̑������Q�S�O�ʂ�ł��邱�Ƃ��킩��B
�y���Q�z
���P�Ɠ��l�A����̂R�s�~�R��̃}�X�ڂɂ��āA���̐F�̌��ߕ��͂Q�S�O�ʂ肠��A���̂X�̃}�X�ڂ̐F�����肷��ƁA�c��̃}�X�ڂ̐F�͈�ӓI�ɒ�܂邩��A�F�̓h����̑����͂�͂�Q�S�O�ʂ�ƂȂ�B
�@�T�̃}�X��(1,2)�C(2,1)�C(2,2)�C(2,3)�C(3,2)�̐F�ԍ������ꂼ��
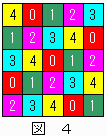
�b(1,2)=0�C�b(2,1)=1�C�b(2,2)=2�C�b(2,3)=3�C�b(3,2)=4�̏ꍇ�ɂ��āA�T�s�~�T�ׂẴ}�X�ڂ̐F�̓h����i�Q�ʂ�j��}�R����ѐ}�S�Ɏ����B
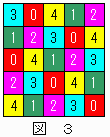 �@
�@
�y���R�z
���P�C���Q�Ɠ��l�ɍl����ƁA�F�̓h����̑����̓}�X�ڂ̑傫���ɂ�����炸�Q�S�O�ʂ�ł��邱�Ƃ��킩��B
�����āA���̓h����̕K�v�\�������͎��̒ʂ�ł���B
�i�T�j���ׂĂ�(a,b)�ɑ��Ăb(a,b)���o0�C1�C2�C3�C4�p
�i�U�j�b(1,2)�C�b(2,1)�C�b(2,2)�C�b(2,3)�C�b(3,2)�͂��ׂĈقȂ�
�i�V�j���́i�@�j�C�i�A�j�̂����ꂩ�����藧��
�i�@�j�ip=a+1 ���� q=b+2�j�܂��́ip=a+2 ���� q=b-1�j�Ȃ�b(a,b)=�b(p,q)
�i�A�j�i��=a+2 ���� q=b+1�j�܂��́ip=a-1 ���� q=b+2�j�Ȃ�b(a,b)=�b(p,q)
�@���ۂɂ́A���Q�ŏ��������悤�ɂT�s�~�T��̃}�X�ڂ̐F��h�邱�Ƃ��ł����Ȃ�A�c��̃}�X�ڂɂ��Ă͂��̂T�s��܂��͂T�̃}�X�ڂƓ����F��h��悢�B
�܂�A���������悤�ɐF��h�����T�s�~�T��̃}�X�ڂ�P�ʂƂ��āA�������^�e�E���R�ɕ��ׂ邱�Ƃɂ���āA�C�ӂ̑傫���̃}�X�ڂɑ���F�̓h�����������B
�������A�s�i�܂��͗�j�̐����T�ɖ����Ȃ��ꍇ�ɂ��ẮA�T�s�i�T��j�̃}�X�ڂɐF��h������Ԃ���s�v�ȍs�i��j����菜���悢�B
�Q�s�~�P�Q��̃}�X�ڂ̓h����̗��}�T�Ɏ����B
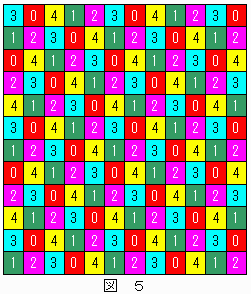
�@�� ���ւ��ǂ�
�@�� ���T�̖����