【コメント】
ナイトツアーを作るには「ワーンスドロフ」の規則を使うのが便利です。
あるマス目から次に飛び移るマス目を次の規則で決定する。
|
つまりできるだけ苦しい状況にあるマス目を先に選んでいるのです。
ただし出発点にはもどってきません。
ちなみに問題4のように、出発点にもどるようなナイトツアーは、nが奇数の時はn×nでは不可能です。
ナイトは白から黒、黒から白に交互に飛び移りますが、nが奇数の場合は白と黒のマス目の個数が異なるからです。
(図1の5×5の場合は白12個、黒13個)
◆参考図書 「ゲームにひそむ数理」 秋山 仁、中村 義作著 森北出版
◆宮城県 アンパンマン さんからの解答
【問題1】(5,5)→(3,4)→(1,5)→(2,3)→(1,1)→
(3,2)→(5,1)→(4,3)→(2,4)→(4,5)→
(5,3)→(4,1)→(2,2)→(1,4)→(3,5)→
(5,4)→(4,2)→(2,1)→(1,3)→(2,5)→
(4,4)→(5,2)→(3,1)→(1,2)→(3,3)
(5,5)→(3,4)→(4,2)→(2,1)→(1,3)→
(2,5)→(4,4)→(5,2)→(3,1)→(1,2)→
(2,4)→(4,5)→(5,3)→(4,1)→(3,3)→
(5,4)→(3,5)→(1,4)→(2,2)→(4,3)→
(5,1)→(3,2)→(1,1)→(2,3)→(1,5)
【問題2】
(1,1)です。
【問題3】
A={(1,5),(5,1),(1,1),(5,5)},
B={(2,3),(4,3),(3,2),(3,4)},
CはAとB以外のマス目だとします。
Aから次の位置に移動できるマス目はBしかありません。
たとえば(1,5)からは(2,3)か(3,4)にしか移動できません。
そのため可能な手順は2つしか考えられません。
ア)全部AとBを通ってからCを通る。
この方法だと時計回りでも、時計と逆回りでも
(2,-1)の方向(0回と指定された方向)は起こってしまいます。
つまりありえません。
イ)Aの一部を通ってからCを通って、またBを通ります。
この手順は最後の位置は(1,5),(5,1),(1,1)にしかなりません。
| b | 4 | |||
| a | 2 | |||
| r | ||||
| 6 | c | |||
| 0 | d |
a+b+c+d=24-6-0-4-2=12
それぞれの方向の数を上の図のようにして、
最後の位置を(y,x)とすると
(6-2)(1,-2)+(4-0)(-2,1)+(a-c)(-1,-2)+(b-d)(-2,-1)
=(y-5,x-5)
m=a-c,n=b-dとすると
m+2n=1−y
2m+n=1-x
| つまり m= | 1−2x+y 3 |
(y,x)∈{(1,5)、(5,1)、(1,1)}とmは整数より
(y,x)=(1,1)であることがわかります。
【問題4】
ありません。
最後にもとの位置に戻るというのは問題3)の イ)のケースになります。
しかしこのケースは最後の位置は
{(1,5)、(5,1)、(1,1)}しかありえないため、もとの位置に戻ることができません。
◆広島県 清川 育男 さんからの解答
【問題1】(5,5)→(4,3)→(5,1)→(3,2)→(1,1)→
(2,3)→(1,5)→(3,4)→(5,3)→(4,1)→
(2,2)→(1,4)→(3,5)→(5,4)→(4,2)→
(2,1)→(1,3)→(2,5)→(4,4)→(5,2)→
(3,1)→(1,2)→(2,4)→(4,5)→(3,3)
(5,5)→(4,3)→(5,1)→(3,2)→(1,1)→
(2,3)→(1,5)→(3,4)→(5,3)→(4,1)→
(2,2)→(1,4)→(3,5)→(5,4)→(4,2)→
(2,1)→(1,3)→(2,5)→(4,4)→(5,2)→
(3,1)→(1,2)→(3,3)→(4,5)→(2,4)
プログラムを組んで探索しました。
【問題2】
( 1, 1) のみ可能。
【問題3】 1
( 3, 4) ( 1, 5) ( 2, 3) ( 3, 1) ( 5, 2)
( 4, 4) ( 2, 5) ( 1, 3) ( 2, 1) ( 4, 2)
( 5, 4) ( 3, 3) ( 1, 2) ( 2, 4) ( 4, 5)
( 5, 3) ( 4, 1) ( 2, 2) ( 1, 4) ( 3, 5)
( 4, 3) ( 5, 1) ( 3, 2) ( 1, 1)
2
( 3, 4) ( 1, 5) ( 2, 3) ( 4, 4) ( 5, 2)
( 3, 1) ( 1, 2) ( 2, 4) ( 4, 5) ( 5, 3)
( 4, 1) ( 3, 3) ( 2, 5) ( 1, 3) ( 2, 1)
( 4, 2) ( 5, 4) ( 3, 5) ( 1, 4) ( 2, 2)
( 4, 3) ( 5, 1) ( 3, 2) ( 1, 1)
3
( 4, 3) ( 5, 1) ( 3, 2) ( 4, 4) ( 5, 2)
( 3, 1) ( 1, 2) ( 2, 4) ( 4, 5) ( 5, 3)
( 4, 1) ( 3, 3) ( 2, 5) ( 1, 3) ( 2, 1)
( 4, 2) ( 5, 4) ( 3, 5) ( 1, 4) ( 2, 2)
( 3, 4) ( 1, 5) ( 2, 3) ( 1, 1) 3通りのようです。
【問題4】
ありません。
【おまけ】
左右対称であるから、152×2=304
全結果はこちらです。
◆千葉県 なのはな子 さんからの解答
【問題1】
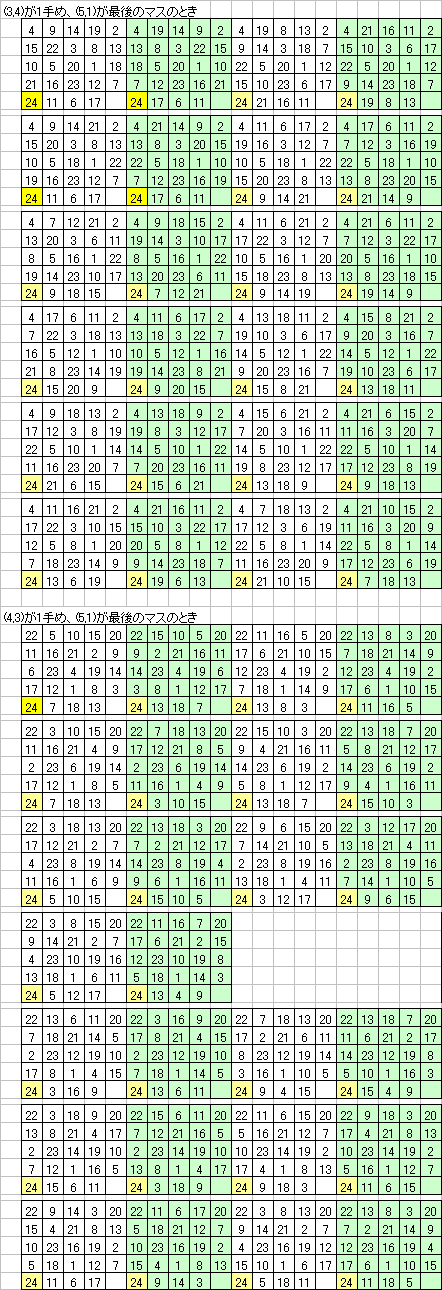
解答は、別表にあります。50通り
(5,1)が最後のマスになる場合です。

【問題2】
(1,1)です。
【問題3】
●理由・・・
行ったことがわかっている方向と回数から、
(5,1)→(3,2)であるとわかります。
そうすると、(4,3)→(5,1)でしかありません。
次に、表のように同じ移動方向を上下左右に対称にならべます。
わかっている方向をすべて当てはめてみます。(図のように)
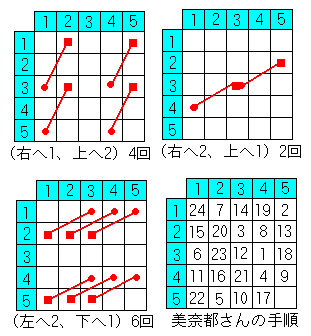
(1,1)(2,4)(4,2)があいています。
最後に移動したマスは、この3つのうちの1つであるとわかります。
(3,4)を1手めとして移動すると、最後に移動するマスは(1,1)になります。
●手順・・・(5,5)(3,4)(1,5)(2,3)(4,4)
(5,2)(3,1)(1,2)(2,4)(4,5)
(5,3)(4,1)(3,3)(2,5)(1,3)
(2,1)(4,2)(5,4)(3,5)(1,4)
(2,2)(4,3)(5,1)(3,2)(1,1)
【問題4】
「ありません」
●理由・・・
24回移動しますから、最後の手順は24回めです。
黒のマスは偶数回に、白のマスは奇数回に通ります。
元の右下は黒のマスです。
そこへ戻る1つ前の手順は必ず白のマスです。
元の右下に戻る1つ前の白のマスが24手めになることは不可能です。
だから、最後に元の右下に戻れるような位置で終わる「ナイトツアー」はありません。
◆愛知県 Y.M.Ojisan さんからの解答
【問題1】(5,5)→(4,3)→(5,1)→(3,2)→(1,1)→
(2,3)→(1,5)→(3,4)→(2,2)→(1,4)→
(3,5)→(5,4)→(4,2)→(2,1)→(1,3)→
(2,5)→(4,4)→(5,2)→(3,1)→(1,2)→
(2,4)→(4,5)→(5,3)→(4,1)→(3,3)
【問題2】
(1,1)のみ
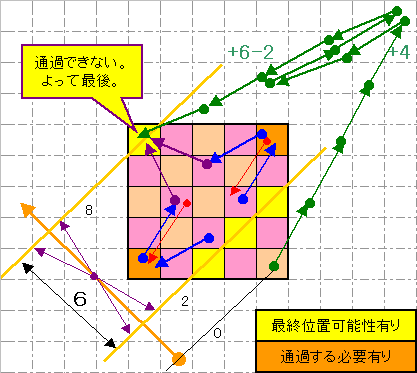
下図のように既知分の手順(緑→)のみでは(1,1)に進む。
即ち(5,5)→(1,1)の方向に対して8単位移動する。
残りの未知の手順(紫→)は合計12手で、(5,5)→(1,1)の方向に対して全部3単位移動なので、結局その方向に6単位とびでしか最終位置はありえない。
即ち,(1,1)または(3,5)(4,4)(5,3)のみである。
これより(5,1)(1,5)は通過しなければならない。
条件より赤→の方向には移動できないので
(5,1)(1,5)の出入りは下図の青→のように1とおりである。
従って(1,1)に対してその方向に向かう移動しかできず、
(1,1)は最後でしかありえない。
【問題3】●
(5,5)→(4,3)→(5,1)→(3,2)→(4,4)→
(5,2)→(3,1)→(1,2)→(2,4)→(4,5)→
(5,3)→(4,1)→(3,3)→(2,5)→(1,3)→
(2,1)→(4,2)→(5,4)→(3,5)→(1,4)→
(2,2)→(3,4)→(1,5)→(2,3)→(1,1)
●
(5,5)→(3,4)→(1,5)→(2,3)→(3,1)→
(5,2)→(4,4)→(2,5)→(1,3)→(2,1)→
(4,2)→(5,4)→(3,3)→(1,2)→(2,4)→
(4,5)→(5,3)→(4,1)→(2,2)→(1,4)→
(3,5)→(4,3)→(5,1)→(3,2)→(1,1)
●
(5,5)→(3,4)→(1,5)→(2,3)→(4,4)→
(5,2)→(3,1)→(1,2)→(2,4)→(4,5)→
(5,3)→(4,1)→(3,3)→(2,5)→(1,3)→
(2,1)→(4,2)→(5,4)→(3,5)→(1,4)→
(2,2)→(4,3)→(5,1)→(3,2)→(1,1)
【問題4】
できない
ナイトは一手毎に白(ベージュ|黄)マスと黒(桃|橙)マスを行き来する。
一方、一周25手は奇数なので、原点には戻れない。
25手目は上図(桃|橙)マスのみ可能。
【おまけ】
304とおり
至って単純なソフトですが、探索計算は短時間で終了しました。
丁度4バイトにマッピングできるところは運が良い。
#include <stdio.h>
#include <stdlib.h>
#include <conio.h>
/* Boad Bit mapping
x x (1) (2) (3) (4) (5)
(1) 31 30 29 28 27
(2) 26 25 24 23 22 21 20
(3) 19 18 17 16 15 14 13
(4) 12 11 10 9 8 7 6
(5) 5 4 3 2 1 0 X
*/
int mask[32];
int next[8] ={9,-5,-13,-15,-9 ,5 ,13,15};//相対移動量
#define INI -1
int tejun[25]={INI};//手順記憶
int position = INI;
int BoadMap = 0x060C1830;// 初期状態ビットマップ
int BoadEND = -1;//FFFFFFFF
int proc(int Level , int BoadMap , int position);
void main()
{
int TE=0;
int i;
for(i=0;i<32;i++) mask[i]=(1<<i);
TE = proc(0 , BoadMap , position);
printf("\n手順の場合数 = %d \n",TE);
getch();
}
int proc(int Level,int BoadMap , int position)
{
int k,newposi,TE=0;
tejun[Level]=position;
if(BoadMap==BoadEND)
return(1); // break setpoint for look in tejun
for(k=0;k<8;k++) //serach
{
newposi= position+ next[k];
if(newposi<0 || newposi>31) continue;
if( (mask[newposi] & BoadMap )!=0) continue;
TE+=proc(Level + 1, BoadMap | mask[newposi] , newposi);
}
if(Level<6) printf("%d %d>",Level,TE);// ticker
return(TE);
}【問題2 コメント】
問題2の条件のうち赤→の方向に進めないのはかなり強い条件である。
問題2の解答から判るように、これだけで
(1,1)または(5,1)、(1,5)が最終位置であるといえる。
このうち、(1,1)以外に関して赤→=0条件だけ適用して可能か考える。
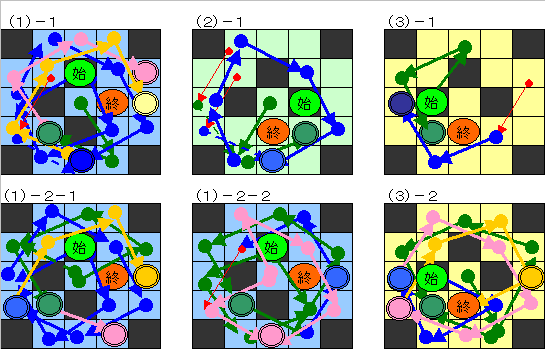
まず直ぐに、下図 (1)〜(3)の3ケースがあることがわかる。
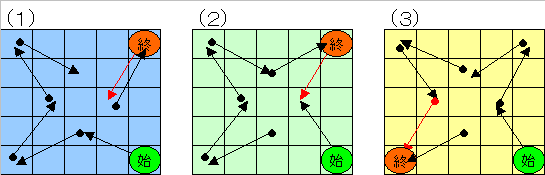
以下詳細は省略するが、それぞれを考えると、下図のようになり(これでは判らないと思いますが御容赦方)、何れも矛盾が生じて不可能であることが判る。
即ち問題2は「赤→=0条件」だけで(1,1)が答えになる。
下図において、黒マスは上図で通過済みマスであり、始点と終点はそれぞれ再構成してある。
(1)のケースは緑の丸に来るのがどちら方向からが可能で、
遡ると
「中央」(3,3)か「始点」(3,2)のどちらが先に来るかで、さらに3タイプに類される。
一方別途 青、黄、ピンクの丸にはどこから来てどこに行くかを、途中分岐がせいぜい2路までで検討した結果を色付矢印で示してある。
その結果、いずれも終点には到達できない等の矛盾に遭遇する。
(2)のケースも同様であるが、タイプは1個だけであり、やはり矛盾が生じる。
(3)のケースもも実際には3タイプあるが、2タイプにまとめてある。
((3)−2図)
やはり矛盾が生じて成立しない。
◆ 問題へもどる
◆ 今週の問題へ