仧嫗搒晎丂K丒H 偝傫偐傜偺夝摎
庤悢俁係庤
庤弴丗
(6,4)仺(4,4)丆(3,1)仺(3,3)丆(4,3)仺(4,5)丆(6,3)仺(4,3)丆(4,3)仺(2,3)丆
(5,4)仺(3,4)丆(4,4)仺(2,4)丆(3,3)仺(3,5)丆(4,1)仺(4,3)丆(5,3)仺(3,3)丆
(4,2)仺(4,4)丆(4,5)仺(2,5)丆(2,4)仺(2,6)丆(6,2)仺(4,2)丆(6,1)仺(4,1)丆
(5,1)仺(5,3)丆(4,3)仺(4,5)丆(4,1)仺(4,3)丆(3,4)仺(3,6)丆(3,2)仺(3,4)丆
(4,4)仺(2,4)丆(4,2)仺(4,4)丆(5,2)仺(5,4)丆(3,6)仺(1,6)丆(3,4)仺(3,6)丆
(3,3)仺(1,3)丆(5,3)仺(3,3)丆(3,5)仺(1,5)丆(5,4)仺(3,4)丆(3,3)仺(3,5)丆
(2,4)仺(1,4)丆(4,4)仺(2,4)丆(4,3)仺(4,4)丆(4,4)仺(4,6)
嵍壓偐傜偺嫍棧傪儅僗栚堦偮侾偲偡傞偲
| 5 | 6 | 7 | 8 | 9 | 10 |
| 4 | 5 | 6 | 7 | 8 | 9 |
| 3 | 4 | 5 | 6 | 7 | 8 |
| 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 1 | 2 | 3 | 4 | 5 |
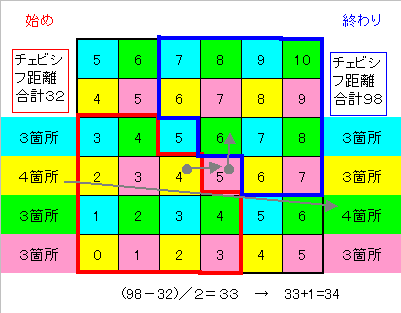
偩偐傜尰嵼偺摓払嫍棧偺崌寁偼俁俀丄
嵟廔摓払嫍棧偼俋俉丄
堦夞偺嵟崅堏摦壜擻嫍棧偼俀偩偐傜
乮俋俉亅俁俀乯亐俀亖俁俁
偱俁俁庤偑嵟抁庤悢偺岓曗偩偑仠 亊 仠 亊 仠 亊
仜 仢 仜 仢 仜 仢
仠 亊 仠 亊 仠 亊
仜 仢 仜 仢 仜 仢
仠 亊 仠 亊 仠 亊
仜 仢 仜 仢 仜 仢
偲報傪偮偗傞偲尰嵼偼仜係丄仢俁丄仠俁丄亊俁偩偑丄
栚揑抧偱偼仜俁丄仢俁丄仠俁丄亊係偺偨傔丄
嵟抁庤悢偼堦庤憹偊偰俁係庤偲側傞丅
惓夝庤弴偼偨偔偝傫偁傞偩傠偆丅
仧媨忛導丂傾儞僷儞儅儞 偝傫偐傜偺夝摎
亂栤戣亃
34庤
(5,3)仺(5,5)丆(6,3)仺(6,5)丆(6,5)仺(4,5)丆(6,4)仺(4,4)丆
(6,1)仺(6,3)丆(5,1)仺(5,3)丆(5,5)仺(3,5)丆(5,4)仺(3,4)丆
(4,4)仺(4,6)丆(3,4)仺(3,6)丆(4,2)仺(4,4)丆(3,1)仺(3,3)丆
(4,3)仺(2,3)丆(3,2)仺(3,4)丆(4,4)仺(2,4)丆(6,2)仺(4,2)丆
(4,1)仺(4,3)丆(4,6)仺(2,6)丆(3,4)仺(1,4)丆(3,3)仺(1,3)丆
(3,6)仺(1,6)丆(4,2)仺(4,4)丆(4,5)仺(2,5)丆(5,2)仺(5,4)丆
(4,3)仺(4,5)丆(6,3)仺(4,3)丆(3,5)仺(1,5)丆(5,4)仺(3,4)丆
(5,3)仺(3,3)丆(3,3)仺(3,5)丆(4,5)仺(4,6)丆(3,4)仺(3,6)丆
(4,3)仺(4,5)丆(4,4)仺(3,4)
亂偍傑偗亃
偢偭偲愭恑乮塃偲忋乯侾儅僗偢偮偟偐摦偐偝側偄応崌丄憤堏摦悢偼摨偠偱
亖3*2+4*4+3*6+2*8+1*10=66
慡晹偺堏摦偼旘傃墇偊傞曽朄偱峴偊偽
66/2=33庤偑嵟抁偱偡丅A B A B A B
C D C D C D
A B A B A B
C D C D C D
A B A B A B
C D C D C D
偡傋偰偺堏摦偑旘傃墇偊傞曽朄偱峴偆偲峫偊傞偲
A偐傜A丄B偐傜B丄C偐傜C丄D偐傜D偺埵抲傊偺堏摦偟偐偱偒傑偣傫丅
偟偐偟尦偺埵抲偼A3儅僗,B3儅僗,C4儅僗,D3儅僗偲怴偟偄埵抲偼A3儅僗,B係儅僗,C俁儅僗,D3儅僗偱偁傞偨傔丄偡傋偰偺堏摦偼旘傃墇偊傞曽朄偱峴偆偙偲偑晄壜擻偱偡丅
偦偺偨傔旘傃墇偊側偄偱堏摦偡傞偺偼彮側偔偲傕俀庤乮嬼悢乯偑昁梫偱偡丅
崌寁亖33-1+2*1=34庤
傛偭偰俁係庤偑嵟抁庤弴偱偡丅
仧垽抦導丂Y.M.Ojisan 偝傫偐傜偺夝摎
亂栤戣夝摎亃
庤悢丂丂丂俁係
(4,1)仺(2,1)丆(4,2)仺(2,2)丆(3,2)仺(1,2)丆(3,1)仺(1,1)丆
(2,1)仺(2,3)丆(1,1)仺(1,3)丆(1,2)仺(1,4)丆(2,2)仺(2,4)丆
(5,3)仺(5,5)丆(6,3)仺(6,5)丆(5,4)仺(5,6)丆(6,4)仺(6,6)丆
(6,5)仺(4,5)丆(6,6)仺(4,6)丆(5,5)仺(3,5)丆(5,6)仺(3,6)丆
(4,5)仺(2,5)丆(4,6)仺(2,6)丆(3,5)仺(1,5)丆(3,6)仺(1,6)丆
(5,1)仺(5,3)丆(6,1)仺(6,3)丆(5,2)仺(5,4)丆(6,2)仺(6,4)丆
(6,3)仺(6,5)丆(5,3)仺(5,5)丆(5,4)仺(5,6)丆(6,4)仺(6,6)丆
(6,5)仺(4,5)丆(6,6)仺(4,6)丆(5,6)仺(3,6)丆(5,5)仺(3,5)丆
(4,3)仺(4,4)丆(4,4)仺(3,4)
亂偍傑偗夝摎亃
乮type侾乯
壓恾嶲徠丅儅僗撪悢抣偼僠僃價僔僃僼嫍棧丅
僠僃價僔僃僼嫍棧偱峫偊傞偲丄嵟戝偱俀乛庤恑傔傞偺偱丄僠僃價僔僃僼嫍棧崌寁抣嵎偐傜俁俁庤偑嵟彫偱偁傞丅
偟偐偟偙偺応崌丄巒傔偲廔傢傝偱丄墿怓偲椢怓偵偁傞嬵偺悢偑崌傢偢偦偺庤偼懚嵼偟側偄丅
傛偭偰丄俁係庤偼嵟彫偱偁傞丅

乮type俀乯
壓恾嶲徠丅儅僗撪偼倃幉曽岦嫍棧丅
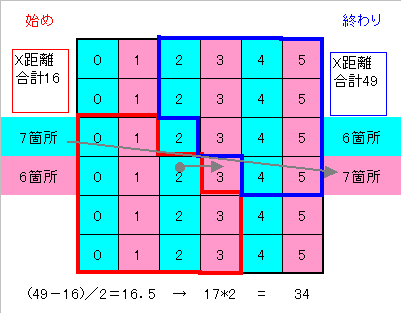
侾庤偱恑傔傞偺偼倃幉丆倄幉壗傟偐偺曽岦偩偗側偺偱丄奺幉曽岦偩偗傪峫偊偰崌寁乮2攞乯偡傞徹柧曽朄傕偁傞丅
偙偺応崌捈愙俁係庤偑嵟彫偲偄偊傞丅
亂俹丏俽丏亃
偍傑偗偼(type2)偺曽偑廫暘偱娙扨偱偡丅
偑丄嵟弶偵尒偊偨偺偑(type1)偱丄徚偡偺偑偍偟偄偺偱夝俀庬偲偟傑偟偨丅
仧搶嫗搒丂偠偭偝傫丂偝傫偐傜偺夝摎
亂栤戣亃
夝摎椺丗俁係庤
(5,3)仺(5,5)丆(6,3)仺(6,5)丆(5,1)仺(5,3)丆(6,1)仺(6,3)丆
(5,4)仺(5,6)丆(6,4)仺(6,6)丆(5,2)仺(5,4)丆(6,2)仺(6,4)丆
(4,1)仺(2,1)丆(4,2)仺(2,2)丆(3,2)仺(1,2)丆(3,1)仺(1,1)丆
(2,1)仺(2,3)丆(1,1)仺(1,3)丆(1,2)仺(1,4)丆(2,2)仺(2,4)丆
(6,5)仺(4,5)丆(6,6)仺(4,6)丆(5,5)仺(3,5)丆(5,6)仺(3,6)丆
(5,3)仺(5,5)丆(6,3)仺(6,5)丆(5,4)仺(5,6)丆(6,4)仺(6,6)丆
(4,5)仺(2,5)丆(4,6)仺(2,6)丆(3,5)仺(1,5)丆(3,6)仺(1,6)丆
(6,5)仺(4,5)丆(6,6)仺(4,6)丆(5,5)仺(3,5)丆(5,6)仺(3,6)丆
(4,3)仺(4,4)丆(4,4)仺(3,4)
亂偍傑偗亃
侾庤偱塃乮嵍乯偵侾曕傑偨偼俀曕恑傓偙偲偑偱偒傞丅
傑偨偼忋乮壓乯偵侾曕傑偨偼俀曕恑傓偙偲偑偱偒傞丅
偙偙偱丄嵍塃偺忋偵偁傞侾乣俇偵懳偟偰僑乕儖抧揰偺崌寁抣偼
俁亊俀亄係亊俁亄俆亊係亄俇亊係亖俇俀
僗僞乕僩抧揰偺崌寁抣偼丄
侾亊係亄俀亊係亄俁亊俁亄係亊俀亖俀俋
侾庤偱嵟戝俀憹偊傞偺偱丄
墶偵摦偐偡嵟彫庤悢偼
乮俇俀亅俀俋乯亐俀亖侾俇丏俆丄
彫悢揰埲壓愗傝忋偘偱侾俈庤丅
忋壓偵娭偟偰傕摨條偵嵟掅侾俈庤偐偐傞丅
侾庤偱偼忋壓丄嵍塃偳偪傜偐偵偟偐摦偐偣側偄丅
廬偭偰丄嵟掅侾俈亄侾俈亖俁係庤昁梫偱偁傞丅
仧搶嫗搒丂BIS 偝傫偐傜偺夝摎
亂偍傑偗亃
嵟彫夞悢丗俁係庤
壖偵憤偰偺堏摦偑僕儍儞僾偱峴偊傞側傜偽
丵丵嘥嘦嘥嘦
丵丵嘨嘩嘨嘩
侾俀丵嘦嘥嘦
俁係俁丵嘨嘩
侾俀侾俀丵丵
俁係俁係丵丵
嵟弶丄晛捠偺悢帤偺応強偵偁偭偨愇偼懳墳偟偨儘乕儅悢帤偺応強偵堏摦偡傞偼偢側偺偱丄晛捠偺悢帤偺悢偲儘乕儅悢帤偺悢偼摨偠偩偗偁傞偼偢乮傢偐傝偢傜偄偐丠乯丅
偟偐偟幚嵺偵偼俀偑俁屄丄俁偑係屄丄嘦偑係屄丄嘨偑俁屄側偺偱丄俁偺応強偵偁偭偨愇偺偆偪侾偮偼 嘦傊堏摦偟側偗傟偽側傜側偄丅
僕儍儞僾柍偟偺堏摦偼嵟彫偵偟偨偄偺偱嘦偐傜嘨傊偺嵟彫偺堏摦悢俀夞偲側傞丅
屻偼慡晹僕儍儞僾偱峴偆偲丄
侾仺嘥丗俉
俀仺嘦丗俉
丂(俇夞偱偄偗傞偑偱偒傞偩偗嵍壓偺傑偡偼奐偗偰偍偔乯
俁仺嘨丗俉
丂(俇夞偱偄偗傞偑偱偒傞偩偗塃忋偺俁偺応強偐傜僕儍儞僾柍偟偺堏摦傪偡傞乯
係仺嘩丗俉
妵屖偺拞偺偙偲偼尩枾側榖偠傖側偄偺偱偄偔傜偱傕梈捠偑偒偔偲巚偆丅
堏摦偼傒傫側塃偐忋曽岦偵摦偔(摉慠丠)丅
傛偭偰俉亊係亄俀亖俁係(夞)
嶲峫傑偱偵丅
(6,3)仺(6,5)丆(5,3)仺(5,5)丆(5,1)仺(5,3)丆(6,1)仺(6,3)丆
(5,4)仺(5,6)丆(6,4)仺(6,6)丆(5,2)仺(5,4)丆(6,2)仺(6,4)丆
(6,6)仺(4,6)丆(5,6)仺(3,6)丆(4,6)仺(2,6)丆(3,6)仺(1,6)丆
(6,5)仺(4,5)丆(5,5)仺(3,5)丆(4,5)仺(2,5)丆(3,5)仺(1,5)丆
(6,3)仺(6,5)丆(5,3)仺(5,5)丆(5,4)仺(5,6)丆(6,4)仺(6,6)丆
(6,5)仺(4,5)丆(6,6)仺(4,6)丆(5,5)仺(3,5)丆(5,6)仺(3,6)丆
(4,2)仺(2,2)丆(4,1)仺(2,1)丆(3,1)仺(1,1)丆(3,2)仺(1,2)丆
(2,1)仺(2,3)丆(1,1)仺(1,3)丆(1,2)仺(1,4)丆(2,2)仺(2,4)丆
(4,3)仺(4,4)丆(4,4)仺(3,4)
丂仧 栤戣傊傕偳傞
丂仧 崱廡偺栤戣傊