『今週の問題』第134回　解答

◆愛知県の中学校３年生　山田太狼 さんからの解答

【問題１】

後手が有利です。

後手は先手が何をうごかしても、カエル３匹のかたまりにするようにします。
そうすると後手が勝ちます。

【問題２】

先手が有利です。

まず先手が１０の所まで最初のカエルを持っていき、そのあと後手が何をうごかしてもその１マスあとにすると勝てます。

◆岐阜県の中学校３年生　お父 さんからの解答

【問題１】

後手が必ず勝ちです。

まず、先手が動かしたら、後手は動かした場所に、３匹がちゃんとならぶようにします。
例えば、

１２３→１２　３→２１３→２　３１→２３１→２３　１→３２１

こういうのはダメです。

１２　３→１　２３

【問題２】

先手が必ず勝ちます。

まず、３のかえるを１０まで動かしてください。
あとは、後手に黄緑のかえるしか動かせないように、後手が動かしたかえるのすぐ後ろに緑のかえるを動かしてください。
これを繰り返していけば先手が勝ちます。

例

１２３→
１２　　　　　　　　３→
１　　　２　　　　　３→
　　　１２　　　　　３→　
　　　　　１　　２　３→
　　　　　　　１２　３→
　　　　　　　１　２３→
　　　　　　　　１２３

◆小学校６年生　香川　愛智　さんからの解答

【問題１】

後手必勝である。

○理由

後手は、常に３個がくっついた状態にして、先手に渡せばよい。

【問題２】

先手は、３番のカエルを１０番に動かす。
後手は、３番から９番のどこかへ動かす。
先手は、そのすぐとなりへ置く。
これをくりかえすと先手が勝つ。

◆長野県の中学校３年生　２００年後の住民 さんからの解答

【問題１】

有利なのは後手。

先手は、後手が３番カエルを動かさない限り、３番カエルしか動かせない。
後手は、先手が３番カエルを動かした後の空いた場所に、１番を３番に、２番を４番に・・・というように、隣のカエルを飛び越して、先手の動かしたカエルとの間に隙間を作らないようにつめていく。
そうすれば確実に勝てると思う・・・。

【問題２】

有利なのは先手。

後手は、先手が２番カエルを動かさない限り、ずっと２番カエルしか動かせない。
先手ははじめに、一気にカエルを１０番へ移動させる。
そして後手に９番をとらせる。
そのために、先手は２番にいたカエルに手をつけないこと。
後手の２番カエルの後に、１番カエルを隙間を作らないようにつめていく。
そうすれば勝てます・・・きっと。

◆広島県　清川 育男 さんからの解答

【問題１】

後手必勝。
後手は３匹のカエルが連続する手を選べばよい。

【問題２】

先手必勝。

先手、先頭のカエルを１マス動かす。
後手は２番目のカエルを動かすしかない。
先手は３番目のカエルを動かし、３匹のカエルを連続させる。
この繰り返しで先手必勝となる。２１手。

4→3→2→5→4→3→6→5→4→7→
6→5→8→7→6→9→8→7→10→9→8　

【問題２別解】

先手が初手で、１０を選択して先頭のカエルを右端に移動させる。
後手が２番目のカエルをどこに移動させても、先手はその後ろに３番目のカエルを移動させる。
したがって、後手に手があれば、そのあとに必ず先手にも手がある。
有限回数のゲ−ムであるから、先手必勝。

この方が、簡明でしょうか、、、。

【おまけ】

先手必勝。

先手は９８３本取る。９８３は素数。
残り１８本。

後手が、

• １（ｐ⁰）本を取るとき、先手は残り１７（素数）本を取って勝ち。

• ２（素数）本を取るとき、先手は残り１６（２⁴）本を取って勝ち。

• ３（素数）本を取るとき、先手は９（３²）本を取って、残り６本にする。

• ４（２²）本を取るとき、先手は８（２³）本を取って、残り６本にする。

• ５（素数）本を取るとき、先手は残り１３（素数）本を取って勝ち。

• ７（素数）本を取るとき、先手は残り１１（素数）本を取って勝ち。

• ８（２³）本を取るとき、先手は４（２²）本を取って、残り６本にする。

• ９（３²）本を取るとき、先手は残り９（３²）本を取って勝ち。

• １１（素数）本を取るとき、先手は残り７（素数）本を取って勝ち。

• １３（素数）本を取るとき、先手は残り５（素数）本を取って勝ち。

• １６（２⁴）本を取るとき、先手は残り２（素数）本を取って勝ち。

• １７（素数）本を取るとき、先手は残り１（ｐ⁰）本を取って勝ち。

後手が、

• １（ｐ⁰）本を取るとき、先手は残り５（素数）本を取って勝ち。

• ２（素数）本を取るとき、先手は残り４（２²）本を取って勝ち。

• ３（素数）本を取るとき、先手は残り３（素数）本を取って勝ち。

• ４（２²）本を取るとき、先手は残り２（素数）本を取って勝ち。

• ５（素数）本を取るとき、先手は残り１（ｐ⁰）本を取って勝ち。

◆宮城県　アンパンマン さんからの解答

【問題１】

後手が有利です。

勝ち方は、後手の番の時にカエル３匹間なく並んでいるようにカエルを動かす。
そのために後手がずっと一番後ろ（一番左側）のカエルを動かす。

【問題２】

先手が有利です。

先手が最初一番右側のカエルを端まで動かす。（１０のマス目）
あとは一番左のカエルをずっと真中のカエルがいるところの一つ左のマス目に動かす。

【おまけ】

先手が有利です。

まず１から１８までの数の中、選べられないのは
６、１０、１２、１４、１５、１８です。

そのなかで６でスタートすると後手が有利。
（先手がどの数字を選んでも負ける）

１０でスタートすると先手が有利。
（先手が４を選ぶ）

１２でスタートすると後手が有利。
（先手がどの数字を選んでも負ける）

１４でスタートすると先手が有利。
（先手が２を選ぶ）

１５でスタートすると先手が有利。
（先手が３を選ぶ）

１８でスタートすると後手が有利。
（先手がどの数字を選んでも負ける）

1001に近い素数は997,991,983です。

先手が997を選ぶ場合、後手が４を選べば後手が勝ちます。
先手が991を選ぶ場合、後手が４を選べば後手が勝ちます。
先手が983を選ぶ場合、18残って、後手がどの数字を選んでも負けます。

つまり勝ち方としては先手が９８３本の棒を取ります。
そのあと６本になるように棒を取ります（数回で）。

後手が取った後、残りの棒は６本より少ない場合、先手がその全部を取ります。

◆愛知県　Y.M.Ojisan さんからの解答

先頭からＴ、Ｍ、Ｌと呼ぶ。

【問題１】

後手必勝

∵先手はＴ，Ｍ移動のみ可能。
これに対し後手は常にＬを移動させる。
この作戦で常にＴＭＬを団子状態にできる。
最終的に先手はＴが右端にある団子状態で受け取り打てなくなる。

【問題２】

先手必勝

∵初手で先手はＴを右端まで移動させる。

後手はＭ移動のみ可能。
これに対し先手は常にＬを最大移動させ、常にＭＬを団子状態にできる。
最終的に後手はＭがＴの直後の団子状態で受け取り打てなくなる。

【おまけ】

先手必勝

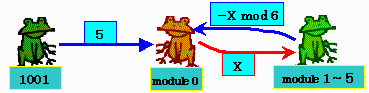
∵　可能な手の集合をＭとする。

１，２，３，４，５∈Ｍであるが、６はＭの要素ではない。

また　∀x∈Ｍ　　x mod 6 ≠０　である。

一方 １００１ mod 6＝５ で　０ mod 6 ＝０である。

よって、先手は初手で　たとえば５個とって、
山の数を９９６即ち６の倍数とする。

以後　後手が　余りｘの手なら
先手は余り6−ｘの手で先手は常に6の倍数に維持でき、
かつ最後まで１〜５個取りの手が可能である。

即ち先手必勝。

　◆ 問題へもどる

　◆ 今週の問題へ

数学の部屋へもどる