『今週の問題』第127回　解答

◆広島県　清川　育男 さんからの解答

こちらをご覧ください。

◆京都府　としひで さんからの解答

【問題１】

解答の一例：

[1]
 13 15 17 19 21 29 28 27
 12 14 16 18 20 22 30 26
 11 45 34 33 32 31 23 25
 10 44 46 35 60 58 57 24
  9 43 36 47 59 61 56 55
  8 42 38 37 48 63 62 54
  7 41 40 39 64 49 51 53
  6  5  4  3  2  1 50 52

左　→左　→左　→左　→左　→上　→上　→上　→
上　→上　→上　→上　→右下→上　→右下→上　→
右下→上　→右下→上　→右下→右下→右下→上　→
上　→上　→左　→左　→右下→左下→左　→左　→
左　→右下→左下→右下→左　→右下→左　→左　→
上　→上　→上　→上　→右下→右下→右下→右下→
右下→上　→右下→上　→上　→上　→左　→上　→
左　→左下→上　→右下→右下→左　→左下→右下

４×４のときの解：

[1]
  1  9  8  7
 16  2 10  6
 15 11  3  5
 14 13 12  4

１６と１を繋げば回路ができているので、スタート地点はどこにとっても構わない。
この事実は、４×４以外の場合に拡張でき、解がスタート地点に関係ないことがわかる。

３×３及び５×５では、虱潰しで解が見つからなかった。

【おまけ２】

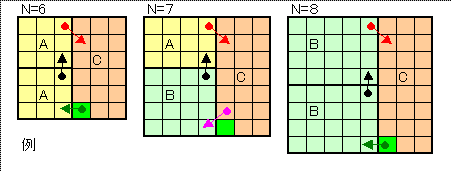
６×６、７×７、８×８、９×９は図のようにできる。

横方向には、第２列の複製で任意の長さに伸ばすことができる。
縦方向は、右側３列は交差線と直線で２枡毎に拡張でき、残りの列は、蛇腹状のパーツを挟み込めば、４枡毎に拡張できる。
よって、図に示すパーツを挟むことによって、任意のｎに対して全ての枡目を通る経路が存在する。

８×８の全経路(turtle.lzh 973KB)です。
サイズがあまりに大きいのでLZH圧縮しました。
解の個数は36732通り、3528秒で求まりました。

前回の方法では７×７で2200秒だったものを、空き領域が分割されるとだめという条件をつけて、22秒くらいまで高速化しました。
それでも８×８では１時間ほどかかってしまいました。
９×９は絶望的です。
解の個数は８×８の40倍くらいになるのではないかと予想してます。

◆愛知県　Y.M.Ojisan さんからの解答

【問題１】

左→上→上→上→上→上→左→左→左下→上→
右下→右下→上→左下→左下→上→右下→右下→上→左下→
右下→左→左→上→左下→上→上→上→上→上→
上→上→右下→上→右下→上→右下→上→右下→上→
右下→右下→右下→上→上→上→左→左→右下→左下→
右下→左下→上→右下→右下→上→左下→左下→上→右下→
右下→上→左下→左

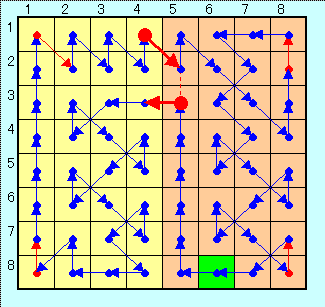
【おまけ１】

N＝３　できない。
N＝５　できない。
N＝４　は１とおり。

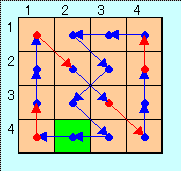
【おまけ２】

下図の３タイプのブロックを組み合わせることにより
N＝４とN≧６の任意の場合を表すことができる。

M=N−3
N=3*Atype個数+4*Btype個数 となるように選ぶ。

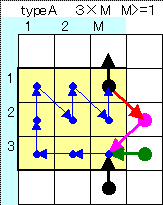
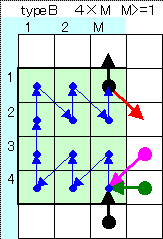
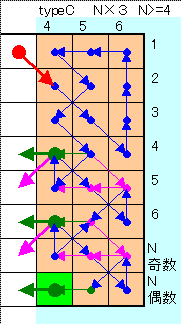
これを下図例のように、同色太矢印のところを重ねて組み合わせる。

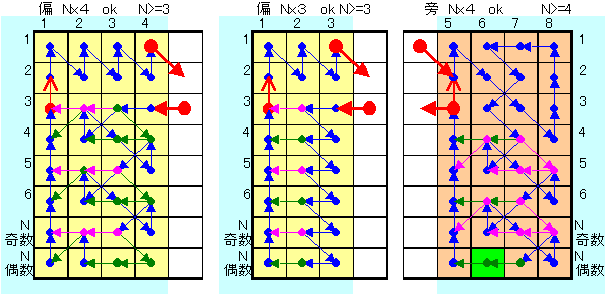
下図ブロックのように横につなぐのもある。
ただしこれは、N=6,9ができない。
解答はこちらによった．

　◆　問題へもどる

　◆　今週の問題へ

数学の部屋へもどる