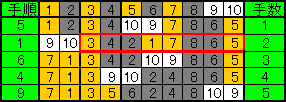
◆千葉県 しまだきよこ さんからの解答
【問題1】
[5→1→6→4→9] 5回
4匹ずつの場合… ---------------------------- A B A B A B A B 〇〇 ---------------------------- A B A B 〇〇A B B A 〇〇A B B A A B B A A A A B B 〇〇B B A A A A 〇〇B B B B A A A A A B B B B 〇〇 ----------------------------【問題2】
[7→3→1→10→4→1] 6回
5匹ずつの場合… ---------------------------- A B A B A B A B A B 〇〇 ---------------------------- A B A B A B 〇〇A B B A A B 〇〇A B B A A B B A 〇〇B A A B B A A B B A B B B A A B B A A 〇〇A B B B 〇〇B B A A A A A 〇〇B B B B B A A A A A ----------------------------【問題3】
[9→5→1→10→4→6→13] 7回
6匹ずつの場合… ---------------------------- A B A B A B A B A B A B 〇〇 ---------------------------- A B A B A B A B 〇〇A B B A A B A B 〇〇A B B A A B B A 〇〇A B B A A B B A A B B A A A A B B A A B B 〇〇B B A A A A 〇〇A A B B B B B B A A A A A A 〇〇B B B B B B A A A A A A A B B B B B B 〇〇 ----------------------------【おまけ】
動物がN匹ずつの場合、入れ替えにかかる最短手数は、(n+1)回です。
Nが2の場合は、できませんでした。
入れ替えの手順は、
まず(A B A B)を(A B B A)に置換え、
次に(B B)と(A A)を左右に振り分けていくのが、一番手っ取り早いと思います。
◆新潟県 エチロ町ヨコリン さんからの解答
【おまけ】
答えはn+1回(n≧3 n:自然数)
n=1の時 0回
n=2の時は できない
n=4以上のときは
n=偶数の時:
| n 2 | 回で12211・・・11221の形にできる。 |
22.11のかたまりで動かすと
| n 2 | 回で1111・・空白・・22221 |
n=奇数の時:
| n+1 2 | 回で1221122・・・11221の形にできる。 |
22.11の塊で動かすと
| n−1 2 | 回で1111空白11222・・・222 |
◆宮城県 アンパンマン さんからの解答
【問題1】
5回
5→1→6→4→9
【問題2】
6回
7→1→8→10→3→11あるいは
7→10→3→9→2→11あるいは
7→3→8→10→1→11
【問題3】
7回
9→5→1→10→4→6→13
【おまけ】
n=1, 0手数
n=2,入れ替える方法はありません。
n=3,最短手数=5
(青木注:4手で可能のようです。手順はY.M.Ojisan さんの解答を参照)
n>3の場合、
ABABAB....ABから
F:AA...ABB...B あるいは
R:BB...BAA...Aにするためには違う側のA、Bを自分の側に持っていかなくてはならない。
| つまり少なくとも2[ | n 2 | ]手数が必要です。 |
実際はn+1手数が必要です。(n>3)
n偶数、n=2mの場合:
最短手数は
2n-3,2n-7,...,1,
2n-2,4,2n-6,8,2n-10,12,...,n,
2n+1
| 合計m+[ | m 2 | ]+[ | m+1 2 | ]+1=n+1手数 |
ちなみにRにするにはn+2手数が必要です。
n=4m+1の場合:
FとRにするための最短手数は同じn+1です。
最短手数は
2n-3,2n-7,...,7,3,
2n-2,2n,1,
2n-6,6,2n-10,10,...,n+3,n-3,
2n+1
合計2m+3+(m-1)+(m-1)+1=n+1手数
(FOOになります)
あるいは
2n-3,2n-7,...,7,3,
1,
2n,4,2n-4,...,n+5,n-1,
1
合計2m+1+m+m+1=n+1手数
(OORになります)
n=4m+3の場合:
最短手数は
2n-3,2n-7,...,7,3,
1,
2n,4,2n-4,10,...,n+7,n-3,n+3,
2n+1
合計(2m+1)+1+(m+1)+m+1=n+1手数
(ROOになります)
ちなみに、Fにするにはn+2手数が必要です。
2n-3,2n-7,...,7,3,
2n-2,2n,1,
2n-6,6,2n-10,10,...,n+1,n-1,
2n+1
合計(2m+1)+3+m+m+1=n+2手数
(FOOになります)
◆愛知県 Y.M.Ojisan さんからの解答
【問題1】 5手

【問題2】 6手

【問題3】 7手
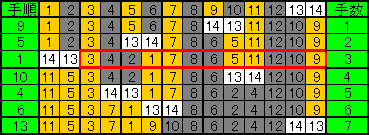
【おまけの予想】
N+1手 (ただしN>2)
N+1手は後述の手順により可能。
N−1手以下は不可能。
「仲間同士隣合い」の数を考えることで証明は容易。
N手はほぼ不可能のようですが、証明できていません。
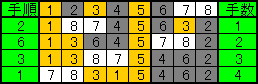
【N=3のとき】 4手
【N=7のとき】 8手
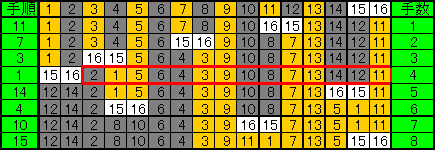
【一般のN(>3)の手順】
(1)枠の右から6番目、
すなわち P1=2N−3 番から始めて
P1−4 、 P1−8 。。。。。と4飛びの位置を移動し、最後に1番を移動する。
なお、Nが奇数のときは1番はP1−4pの系列ではない。
すると、必ず、[(N+1)/2]手で、解答図内赤枠のように、両端が単独かつ右端がライオンで、間は2匹ずつ交互に整列する状態になる。
細かく見ると、Nの偶奇性で動物左端(空白のとなり)がライオンかねずみか決まる。
解答図参照。
(2− 奇数N)
枠の右から3番目、
すなわち P2=2N 番から始めて、空白を外側から中心へ仲間が増えるように移動させる。
すなわち P2,4,P2−4,8,。。。。。。というように移動させる。
すると、合計N手めで、 解答図{問題2、 N=7のとき}に示されるように、リーチ手になり、
最後に(N+1)/2の偶奇性により、右端2N+1番 または 左端1番を移動して完成。
すなわちN+1手で完成。
(2− 偶数N)
枠の右から5番目、
すなわち P2=2N−2 番から始めて、空白を外側から中心へ仲間が増えるように移動させる。
すなわち P2,4,P2−4,8,。。。。というように移動させる。
すると、合計N手めで、 解答図{問題1、 問題3}に示されるように、
{ライオンN−1匹+空白2+ねずみN匹+ライオン1匹}のリーチ手になり、
最後に右端の2N+1番を移動して完成。
すなわちN+1手で完成。
まとめると、Nの4の剰余により若干異なる4タイプがあるが、概念的には同じ手順
{右から4飛びで左へ、1番、右から始めてV字状に中心へ、最後に完成の1手}により
N+1手で完成させることができる。
◆ 問題へもどる
◆ 今週の問題へ