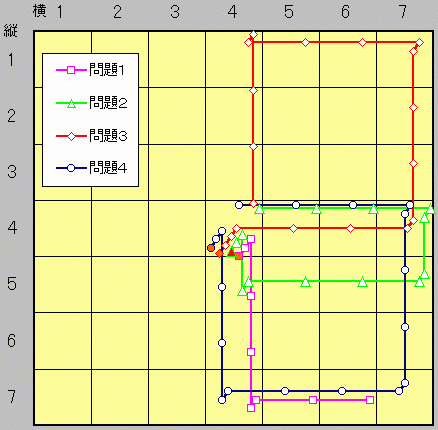
◆愛知県 Y.M.Ojisan さんからの解答
【問題1】 8回
左→左→前→前→前→左→前→前
【問題2】 13回
左→左→前→左→前→前→前→左→前→左→前→前→前
【問題3】
(1,7) 18回
【問題4】
17回のものは(7,7)のみ

◆長野県 Mr.D さんからの解答
【問題1】 8回
【問題2】 13回
【問題3】 (1,7)
【問題4】 (7,7)
【問題2】以降では、それぞれのマス目まで行って帰るときの、前に進む回数と左に回転する回数を求めてみました。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 1 | 12 | 10 | 8 | 6 | 8 | 10 | 12 |
| 2 | 10 | 8 | 6 | 4 | 6 | 8 | 10 |
| 3 | 8 | 6 | 4 | 2 | 4 | 6 | 8 |
| 4 | 6 | 4 | 2 | 0 | 2 | 4 | 6 |
| 5 | 8 | 6 | 4 | 2 | 4 | 6 | 8 |
| 6 | 10 | 8 | 6 | 4 | 6 | 8 | 10 |
| 7 | 12 | 10 | 8 | 6 | 8 | 10 | 12 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 1 | 3 | 3 | 3 | 2 | 6 | 6 | 6 |
| 2 | 3 | 3 | 3 | 2 | 6 | 6 | 6 |
| 3 | 3 | 3 | 3 | 2 | 6 | 6 | 6 |
| 4 | 3 | 3 | 3 | 0 | 5 | 5 | 5 |
| 5 | 4 | 4 | 4 | 4 | 5 | 5 | 5 |
| 6 | 4 | 4 | 4 | 4 | 5 | 5 | 5 |
| 7 | 4 | 4 | 4 | 4 | 5 | 5 | 5 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 1 | 15 | 13 | 11 | 8 | 14 | 16 | 18 |
| 2 | 13 | 11 | 9 | 6 | 12 | 14 | 16 |
| 3 | 11 | 9 | 7 | 4 | 10 | 12 | 14 |
| 4 | 9 | 7 | 5 | 0 | 7 | 9 | 11 |
| 5 | 12 | 10 | 8 | 6 | 9 | 11 | 13 |
| 6 | 14 | 12 | 10 | 8 | 11 | 13 | 15 |
| 7 | 16 | 14 | 12 | 10 | 13 | 15 | 17 |
◆岡山県の高校生 aki5 さんからの解答
【問題1】
A.8回
例 左→左→前→前→前→左→前→前
【問題2】
A.13回
例 左→左→前→左→前→前→前 [この時亀は(5,7)にいる] →左→前→左→前→前→前【問題3】
A.(1,7)
亀は中央(4,4)にいるので、最長距離は4隅の(1,1)(1,7)(7,1)(7,7)である。
1マスの距離を1とすると、再び中央に戻ってくるまでの最長距離は12となる。
亀は左回転しかできないので、最も命令の必要になる場所は、亀が右回転しかできない時に命令が最も少なくなる場所と言い換えられる。
よって(1,7)が最も適している。
例 左→左→左→前→前→前→左→前→前→前 [この時亀は(1,7)にいる] →左→前→前→前→左→前→前→前 【18回】【問題4】
A.(7,7)
問題3の命令回数より1回だけ減らせばよい。
この時、(距離を1減らした時の命令数)<(向きを変える回数を1回減らした時の命令数)となるので、問題3の始めに左を向く回数を1回分減らすと良い。
この時亀は(7,7)に行く。
例 左→左→前→前→前→左→前→前→前 [この時亀は(7,7)にいる] →左→前→前→前→左→前→前→前 【17回】
◆愛知県 永井 拓也 さんからの解答
亀は左にしか曲がれないから,反時計周りに円を書くように移動する事で最短の移動ができる.
【問題1】
左→左→前→前→前→左→前→前
【問題2】
左→左→前→前→前→左→前→左→前→前→前→左→前
移動に最も多くの命令が必要なのは,四つの角 (1,1), (1,7), (7,1), (7,7) の何れかである.
(4,4) から角に行って戻ってくるのには,最初に進む方向が決まれば前進が 12 回と左回りが 3 回あれば良い.
そのため,最初に前進する為に回転させる数によって,命令数が決まる.
【問題3】
(1,7) 命令数 18
左→左→左→前→前→前→左→前→前→前→左→前→前→前→左→前→前→前
【問題4】
(7,7) 命令数 17
左→左→前→前→前→左→前→前→前→左→前→前→前→左→前→前→前
◆福岡県 古豚 さんからの解答
【問題1】
左→左→前→前→前→左→前→前 で8回
【問題2】
左→左→前→左→前→前→前→左→前→左→前→前→前 で13回
【問題3】
(1,7)の18回
【問題4】
(7,7)の17回
問題2〜4
元の位置に戻る最短手数は、移動こま数と4方向転換が必要。
方向転換が左回りなので、左回りにこま移動できるように先に方向転換し、その後に左回りに1周すればよい。
◆東京都 まさくん さんからの解答
【問題1】
8回
左→左→前→前→前→左→前→前
【問題2】
13回
左→左→前→左→前→前→前→左→前→左→前→前→前
【問題3】
(1,7) 18回
左→左→左→前→前→前→左→前→前→前→左→前→前→前→左→前→前→前
中央から一番遠いマスは、4つの端(1,1)(1,7)(7,1)(7,7)のどれかになります。
4つの端から中央のマスへ戻る命令は、どの地点からでも同じ回数なので、スタート時に、最も回転する必要のある地点が最も命令が多くなります。
【問題4】
(7,7) 17回
左→左→前→前→前→左→前→前→前→左→前→前→前→左→前→前→前
問題3より、回転する命令を1回少なくして到達するマスは(7,7)になります。
【感想】
問題4で(1,7)の近辺の(1,6)や(2,7)もどうか考えてみましたが、必ず2回分少なくなってしまうので、(7,7)だけという結論になりました。
◆ 問題へもどる
◆ 今週の問題へ