◆千葉県の小学生 緑川 敦 さんからの解答
【問題1】 1
【問題2】 3
【問題3】 33
【感想】
問題1,2は,簡単だったけど,問題3はちょっと難しかった。
◆千葉県 緑川 正雄 さんからの解答
【問題4の回答】 641
【問題4の理由】
(1)
1〜4までの数字が並んでいるとき、
2,4,1が消えて3が残る。
(2)
1〜8までの数字が並んでいるとき、最後に残る数字
2,4,6,8までの4個の数字を消した後に残る4個の数字
7,5,3,1の3番目[(1)より]
即ち、7-2×(3-1)=3
(3)
1〜16までの数字が並んでいるとき、最後に残る数字
2,4,…,16までの8個の数字を消した後に残る8個の数字
15,13, …,3,1の3番目[(2)より]
即ち、15-2×(3-1)=11
(4)
1〜32までの数字が並んでいるとき、最後に残る数字
2,4,…,32までの16個の数字を消した後に残る16個の数字
31,29,....,3,1の11番目[(3)より]
即ち、31-2×(11-1)=11
(5)
1〜63までの数字が並んでいるとき、最後に残る数字
2,4,…,62までの31個の数字を消した後に残る32個の数字
63,61,....,3,1の11番目[(4)より]
即ち、63-2×(11-1)=43
(6)
1〜126までの数字が並んでいるとき、最後に残る数字
2,4,…,126までの63個の数字を消した後に残る63個の数字
125,123,....,3,1の43番目[(5)より]
即ち、125-2×(43-1)=41
(7)
1〜251までの数字が並んでいるとき、最後に残る数字
2,4,…,250までの125個の数字を消した後に残る126個の数字
251,249,....,3,1の41番目[(6)より]
即ち、251-2×(41-1)=171
(8)
1〜501までの数字が並んでいるとき、最後に残る数字
2,4,…,500までの250個の数字を消した後に残る251個の数字
501,499,....,3,1の171番目[(7)より]
即ち、501-2×(171-1)=161
(9)
1〜1001までの数字が並んでいるとき、最後に残る数字
2,4,…,1000までの500個の数字を消した後に残る501個の数字
1001,999,....,3,1の161番目[(8)より]
即ち、1001-2×(161-1)=681
(10)
1〜2001までの数字が並んでいるとき、最後に残る数字
2,4,…,2000までの1000個の数字を消した後に残る1001個の数字
2001,1999,....,3,1の681番目[(9)より]
即ち、2001-2×(681-1)=641
◆東京都 藤本 さんからの解答
【問題1】
1 が残る
2,4,6,3,5 の順に消える
【問題2】
3 が残る
2,4,6,5,1,7 の順に消える
【問題3】
33 が残る
解法:
ここまでは力ずくで求めました
消える順は省きます。
【問題4】
641 が残る
解法:
1から25ぐらいまでの消え方を解析した結果、以下の方法で求めました。
2001=210+29+28+27+26+24+1
と書いたとき に べきが2以上の偶数の項を省いてえられる
29+27+1=641
が最後に残る
一般的には
1〜Nの数がならんでいるとき
|
となるのではないでしょうか?
(証明はできていません)
◆福岡県 Mulls さんからの解答
【問題4】
P1=1、2、3、、、2001を→方向に消した場合
2n-1(n=1、2、、、1001)が残る
次に2001から←方向に消す場合
2001=2n-1 (n=2*501-1)であるので
2(2n−1)-1 (n=1、2、、、501)が残る
このnの列をP2=1、2、、、501とし、上記の操作を繰り返す。
→方向
残る数字は1、3、、、501 2k−1(k=1、2、、251)
←方向
501=2k−1 (k=2*126-1)であるので
2(2k−1)-1 (k=1、2、、、126)
同様にこのnを次の列P3=1、2、、、126とする。
→方向
残る数字は1、3、、、125 2n−1(m=1、2、、63)
→方向
125=2m−1 (m=2*32-1)であるので
2(2m−1)-1 (m=1、2、、、32)
ここまでくればすぐに紙に書いて答えが出る。
答えは11
上記から
P4=4(4(4N-3)-3)-3(N=1、2、、、32)
N=11なので、最後に残る数字は641である。
◆愛知県 Y.M.Ojisan さんからの解答
【問題1】
6のとき 1
【問題2】
7のとき 3
【問題3】
50のとき 33
【問題4】
2001のとき 641

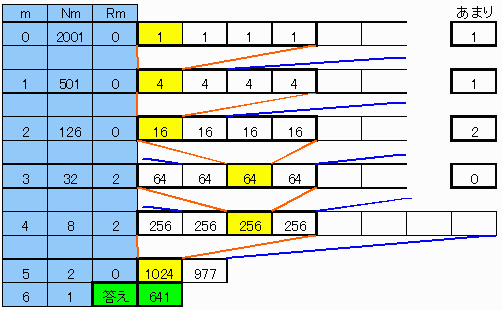
往復を1セットにして、左から4個づつくぎり、右に残る4の剰余個により左側のどこが残るか計算すればよい。
[ ]:ガウス記号を用いて下式で残る番号がわかる。
N0=初項( 例:2001 )
| Rm=2×[ | (Nm−1) mod 4 2 | ] |
| Nm+1=[ | Nm−1 4 | ]+1 |
| 答え=1+ | Nm+1=1になるmまで Σ m=0 | {4m×Rm} |
◆広島県 清川 育男 さんからの解答
1〜2002までの全結果です。
◆東京都 じっさん さんからの解答
【問題1】
偶数と、それから1引いた奇数は、結果が同じになります。
1
【問題2】
3
2,4,6,5,1,7の順に消えて、3が残ります。
【問題3】
33
1回目で2,4,6,...,50が消え、
2回目で47,43,39,...,3が消え、
3回目で5,13,21,...,45が消え、
4回目で41,25,9が消え、
5回目で17,49が消え、
6回目で1が消え、33が残ります。
【問題4】
641
手順:
1.元の数字から1を引く。
例:2001→2000
2.2進数にする。
例:2000(10)→11111010000(2)
3.下から奇数の位の数をゼロにする。
例:11111010000(2)→01010000000(2)
4.10進数にする。
例:01010000000(2)→640(10)
5.1を足す。
例:640→641
考え方:
奇数回目は、下から2個目,4個目,...偶数個目が消えます。
偶数回目は、右から消すので,
奇数個の時は、下から偶数個目が消えます。
偶数個の時は、下から奇数個目が消えます。
次に、最初に1からnまで並んでいる場合にk回目の開始時に偶数個残っているのか奇数個残っているのかを考えます。
1回目は、nを2で割って、
余りが1の場合、奇数個です。
余りが0の場合、偶数個です。
2回目は、nを4で割って、
余りが1,2の場合、奇数個です。
余りが3,0の場合、偶数個です。
3回目は、nを8で割って、
余りが1,2,3,4の場合、奇数個です。
余りが5,6,7,0の場合、偶数個です。
4回目は、nを16で割って、
余りが1〜8の場合、奇数個です。
余りが9〜15,0の場合、偶数個です。
k回目は、nを2kで割って、
前半、つまり余りが1〜2k-1の場合、奇数個です。
後半、つまり余りが2k-1+1〜2k−1,0の場合、偶数個です。
考えやすくするために、最初にnから1を引きます。
すると、余り0〜2k-1−1が前半、残りが後半になります。
これを2進法で示すと、1つ下の桁が0の場合前半、1の場合後半になります。
また、
奇数回目は、余りに関わらず、必ず前半が残ります。
偶数回目は、余りが前半の場合は前半、余りが後半の場合は後半が残ります。
従って、元の数から1を引いて2進数で表した後、
奇数回目、すなわち下から奇数桁目は全て前半が残るので0にする。
偶数回目、すなわち下から偶数桁目はそのまま残るので0,1はそのままにする。
最後に、最初に引いた1を足して元に戻す。
で、上に書いた手順(1〜5)になります。
ちなみに、手順3終了時の2進数は、桁数が何回の操作で1個になるかを示し、下からk桁目がk回目の操作を示します。
各桁については、0が前半が残ることを示し、1が後半が残ることを示します。
◆ 問題へもどる
◆ 今週の問題へ