◆宮城県 アンパンマン さんからの解答
【問題1】
(1) 8,左 (2) 4,右
(3) 7,左 (4) 5,右
(5) 1,右 (6) 12,左
【問題2】
(1) 9,右 (2) 8,左
(3) 4,右 (4) 6,右
(5) 10,左 (6) 7,右
(7) 1,右
【おまけ】
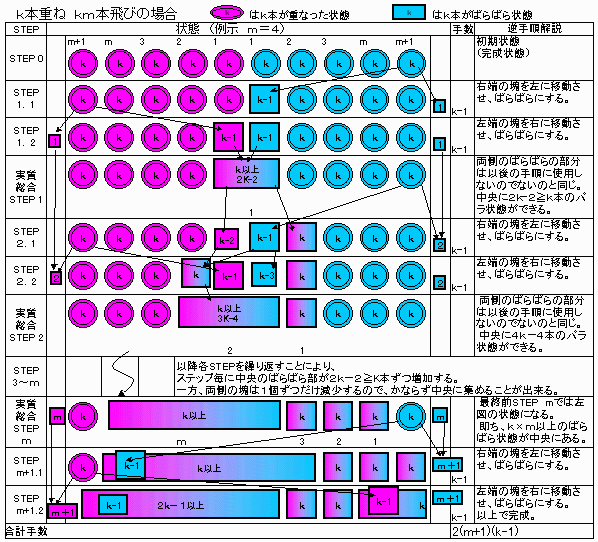
完成した時を考えると、マッチが一番少ない本数のときは最後の移動は端っこに移動させるべきです。
端っこに動くためには真ん中のkmマッチが必要です。
なので、飛び越す山(完成したk本が重ねたm組)の数を考慮します。
一番少ない場合、山が一つ、つまり最後の飛び越しは端っこから反対側の端っこに移動させることで、
マッチがkm+k本。
両端があるので一つの端っこから反対側の端っこに移動させるには真ん中のk本が重ねたm組が必要です。
その真ん中のm組を作るのに、それぞれkm本のマッチを飛び越さなきゃいけません。
でもその真ん中の一本のマッチをもとの位置に戻そうとすることはできません。
なぜなら、飛び越せるマッチは多くてもk(m-1)+1本しかありません。
( k(m-1)+1 < km )
つまり矛盾です。
ということはそれぞれの端を完成させるためには別々の真ん中のマッチを移動させることしかないのです。
つまり山が二つあって、全部で2k(m+1)です。
例)
1 キ キ 1 1 1 1 キ キ 1 ( k=3、m=2)
飛び越す方法は最初は
k(2m+1)と m+1 の位置に重ねさせる
(一本ずつ交互に、右の位置(つまりk(2m+1))は左のマッチを移動させ、左の位置は右のマッチを移動させる)。
k本重ねたら、次はk(2m+1)+1とmの位置に同じように重ねさせる。
次はk(2m+1)+2とm-1の位置、...、
最後は2k(m+1)-1と2の位置です。
そのあと、残りの真ん中のマッチを両端に移動させれば完了です。
つまり可能となるマッチ棒は最低2k(m+1)本です。
◆長野県 Mr.D さんからの解答
【問題1】
(1) 8,左(2) 4,右(3) 7,左
(4) 5,右(5) 6,左(6) 9,右
【問題2】
(1) 6,左(2) 10,左(3) 5,右(4) 9,左
(5) 7,右(6) 8,左(7) 11,右
【おまけ】
本数 2k(m+1)本
手順
1段階 左からm+1本目にk本重なるようにする。
2段階 右からm+1本目にk本重なるようにする。
3段階 左からm本目にk本重なるようにする。
4段階 右からm本目にk本重なるようにする。
・・・・・・
2m+1段階 左から1本目にk本重なるようにする。
2m+2段階 右から1本目にk本重なるようにする。
それぞれの段階は、k-1回ずつの移動があります。
それぞれの段階の手順は1通りしかないので、これでどうでしょうか。
上の手順で動かすと、k=3,m=2の場合は下のようになります。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 3 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 3 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 2 | 1 | 1 |
| 1 | 1 | 3 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 3 | 1 | 1 |
| 1 | 2 | 3 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 3 | 1 | 1 |
| 1 | 3 | 3 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 3 | 1 | 1 |
| 1 | 3 | 3 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 3 | 2 | 1 |
| 1 | 3 | 3 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 3 | 3 | 1 |
| 2 | 3 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 3 | 3 | 1 |
| 3 | 3 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 3 | 3 | 1 |
| 3 | 3 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 3 | 3 | 2 |
| 3 | 3 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 3 | 3 |
k毎にmを変えてこのようなものを書くと、親子のようにきれいになりました。
◆愛知県 Y.M.Ojisan さんからの解答
【問題1】
(1) 5,右 (2) 9,左
(3) 6,右 (4) 8,左
(5) 7,右 (6) 4,左
【問題2】
(1) 6,左 を実行して12本の「問題1」に転化。i.e.
(2) 7,右 (3) 11,左 (4) 8,右
(5) 10,左 (6) 9,右 (7) 5,左
【おまけ】
マッチの最小数は 2(m+1)k 本
○十分条件
つまり手順を以下に示す。
但し思考過程と同じ逆手順を示す。

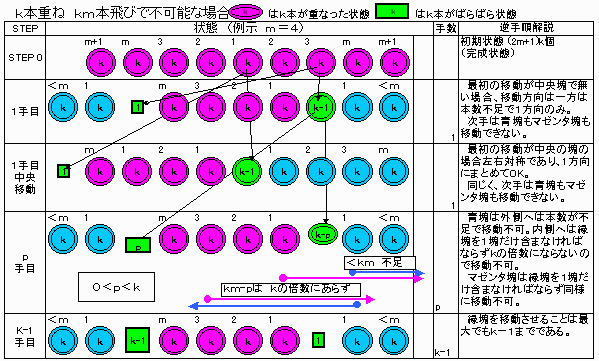
○必要条件
kn本が可能であるとき、最初にk本を端に移動させることは常に可能であるので、
k(n+1)は可能である。
よって、k(2m+1)本では不可能であることのみを示せばよい。
手順は可逆的であるので、逆手順で考える。
(a)本数不足 か
(b)含まれる本数pが1〜k−1である緑塊を1個必ず含まなければならずkの倍数にはならない。
即ち、km本を飛び越すことが出来ない。
従って、移動できない。
◆東京都 藤本 さんからの解答
【問題1】
(1) 8,左 (2) 4,右
(3) 7,左 (4) 5,右
(5) 6,左 (6) 9,右
【問題2】
(1) 9,右 (2) 8,左
(3) 4,右 (4) 7,左
(5) 5,右 (6) 6,左
(7) 10,右
【おまけ】
2(m+1)k本
(つまり k本の束が 2(m+1)個できる マッチ棒が必要)
手順
概略は以下のとおり
(1) (m+1)番目のマッチに重なるように (k-1)本を左に動かす (2) (2k(m+1)-m)番目(右から(m+1)番目)のマッチに重なるように (k-1)本を右に動かす (3) m番目のマッチに重なるように (k-1)本を左に動かす (4) (2k(m+1)-m+1)番目(右からm番目)のマッチに重なるように (k-1)本を右に動かす …… (2m+1) 1番目のマッチに重なるように (k-1)本を左に動かす (2m+2) 2k(m+1)番目(右端)のマッチに重なるように (k-1)本を右に動かす このように 両端から(m+1)番目,m番目、(m-1)番目…の順で 両端のマッチ棒までが k本重なるように 端のほうに向かって 左・右の順で(k-1)本動かす
◆東京都 まさくん さんからの解答
【問題1】
(1) 5,右 (2) 9,左
(3) 6,右 (4) 8,左
(5) 7,右 (6) 4,左
【問題2】
(1) 9,右 (2) 5,右
(3) 10,左 (4) 6,右
(5) 8,左 (6) 7,右
(7) 4,左
今までのマッチ棒問題と同様に、最後の1手前がどうなるか予想します。
すると、1−2−2−1 の組ができるとよいことがわかります。
問2も今までと同様に、先に2本組を端に作ってしまい、残りを12本にしてしまうと、問1と同じ形になります。
いろいろ試してみた結果、今回は2本組を作る際、内側の2本を先に作ってから2本を飛び越す形で残りの2本組を作らないと、うまく完成できませんでした。
【おまけ】
今までのマッチ棒問題と同様に、最後の1手前を考えたとき、どの場合も
(k−1)、k、k・・・k、k、1
(k本の組がm個)
という並びが2組必要です。
このときの本数は、
2(km+k−1+1)=2k(m+1)本となります。
◆ 問題へもどる
◆ 今週の問題へ