◆広島県 清川 育男 さんからの解答
【問題1】
(1)A→B (2)C→B (3)A→C (4)B→C
(5)B→C (6)A→B (7)C→B (8)C→B
(9)C→A (10)C→A (11)B→A (12)B→A
(13)C→B (14)A→C (15)A→C (16)A→B
(17)A→B (18)C→B (19)C→B
19手。
【問題2】
(1)A→C (2)A→B (3)C→A (4)C→A
(5)C→B (6)A→B (7)A→B (8)A→C
(9)B→A (10)B→A (11)B→C (12)B→C
(13)A→C (14)A→C (15)A→B (16)C→A
(17)C→A (18)C→B (19)C→B (20)A→B
(21)A→B (22)C→A (23)C→A (24)B→C
(25)B→C (26)B→A (27)B→A (28)C→A
(29)C→A (30)C→B (31)A→B (32)A→B
(33)A→C (34)A→C (35)B→C (36)B→C
(37)A→B (38)A→B (39)C→A (40)C→A
(41)C→B (42)C→B (43)A→B (44)A→B
44手。
【問題3】
(1)A→B (2)C→B (3)A→C (4)B→C
(5)B→C (6)A→B (7)C→B (8)C→B
(9)C→A (10)C→A (11)B→A (12)B→A
(13)C→B (14)A→C (15)A→C (16)A→B
(17)A→B (18)C→B (19)C→B (20)A→C
(21)B→C (22)B→C (23)B→A (24)B→A
(25)C→A (26)C→A (27)B→C (28)B→C
(29)A→B (30)A→B (31)A→C (32)A→C
(33)B→C (34)B→C (35)A→B (36)C→B
(37)C→B (38)C→A (39)C→A (40)B→A
(41)B→A (42)C→B (43)C→B (44)A→C
(45)A→C (46)A→B (47)A→B (48)C→B
(49)C→B (50)C→A (51)C→A (52)B→A
(53)B→A (54)B→C (55)B→C (56)A→C
(57)A→C (58)B→A (59)B→A (60)C→B
(61)C→B (62)C→A (63)C→A (64)B→A
(65)B→A (66)C→B (67)A→C (68)A→C
(69)A→B (70)A→B (71)C→B (72)C→B
(73)A→C (74)A→C (75)B→A (76)B→A
(77)B→C (78)B→C (79)A→C (80)A→C
(81)A→B (82)A→B (83)C→B (84)C→B
(85)C→A (86)C→A (87)B→A (88)B→A
(89)C→B (90)C→B (91)A→C (92)A→C
(93)A→B (94)A→B (95)C→B (96)C→B
96手
【問題4】
0,2,7,19,44,96,201,413,838,1690,
上記の数列が予想されます。
漸化式は、下記が予想されます。
A(0)=0,A(1)=2
| A(n)=3*A(n-1)-2*A(n-2)+ | 3-(-1)n 2 |
一般項を求めることが出来ました。
| A(n)= | 40*2n-18*n-39-(-1)n 12 |
| 0 | 2 | 7 | 19 | 44 | 96 | 201 | 413 | 838 | 1690 | 3395 | 6807 | |||||||||||
| 2 | 5 | 12 | 25 | 52 | 105 | 212 | 425 | 852 | 1705 | 3412 | ||||||||||||
| 3 | 7 | 13 | 27 | 53 | 107 | 213 | 427 | 853 | 1707 |
階差数列の階差数列は数列サイトに掲載されています。
素数とも関係ある面白そうな数列のようです。
ID Number: A048573 Sequence: 2,3,7,13,27,53,107,213,427,853,1707,3413,6827,13653,27307, 54613,109227,218453,436907,873813,1747627,3495253,6990507, 13981013,27962027,55924053,111848107,223696213,447392427, 894784853,1789569707 Name: a(n) = a(n-1) + 2a(n-2), a(0)=2, a(1)=3. Program: (PARI) a(n)=(5*2n+(-1)n)/3 (PARI) a(n)=if(n<2,n+2,a(n-1)+2*a(n-2)) See also: a(n) = 2n+1-A001045(n). Keywords: nonn Offset: 0 Author(s): Michael Somos (somos@grail.cba.csuohio.edu)
【おまけ】
階差数列がベル数、スターリング数、パスカルの三角形等に関係します。
以前「水の流れさん」のH.Pで取り上げらました。
「迷路」の問題とも考えられると思います。
完成が迷路を抜け出した状態。
したがって、最小手順を問題にしなければ、機械的に出来ます。
2,7,21,61,175,・・・
N=3
(1)A→B (2)C→B (3)C→A (4)B→A
(5)B→A (6)C→B (7)A→B (8)A→B
(9)A→C (10)A→C (11)B→A (12)B→C
(13)A→C (14)A→B (15)C→A (16)C→A
(17)C→B (18)C→B (19)A→C (20)A→B
(21)C→B
N=4
(1)A→C (2)A→B (3)C→B (4)C→A
(5)B→A (6)C→B (7)A→C (8)A→B
(9)C→B (10)C→A (11)B→A (12)B→C
(13)A→C (14)B→A (15)B→A (16)C→A
(17)C→A (18)C→B (19)A→C (20)A→C
(21)A→B (22)A→B (23)C→A (24)C→B
(25)A→B (26)A→C (27)A→C (28)B→A
(29)B→C (30)A→C (31)B→A (32)B→A
(33)C→A (34)C→B (35)A→B (36)A→C
(37)A→C (38)B→A (39)B→C (40)A→C
(41)A→B (42)C→B (43)C→B (44)C→A
(45)C→A (46)B→C (47)B→A (48)C→A
(49)C→B (50)C→B (51)A→C (52)A→B
(53)C→B (54)A→C (55)A→C (56)B→A
(57)B→A (58)C→B (59)C→B (60)A→B
(61)A→B
N=5
(1)A→C (2)A→B (3)C→B (4)C→A (5)B→A (6)C→B (7)A→C (8)A→B (9)C→B (10)A→C (11)B→A (12)B→C (13)A→C (14)B→A (15)B→A (16)C→A (17)C→A (18)C→B (19)C→B (20)A→C (21)A→B (22)C→B (23)A→C (24)A→C (25)B→C (26)B→A (27)C→A (28)C→B (29)C→B (30)A→C (31)A→B (32)C→B (33)C→A (34)B→A (35)B→C (36)A→C (37)B→A (38)B→A (39)C→A (40)C→B (41)A→B (42)A→C (43)A→C (44)B→A (45)B→C (46)A→C (47)B→A (48)B→A (49)C→B (50)C→B (51)C→A (52)C→A (53)B→C (54)B→A (55)C→A (56)C→B (57)A→B (58)A→B (59)A→C (60)A→C (61)B→A (62)B→C (63)A→C (64)A→B (65)A→B (66)C→A (67)C→B (68)A→B (69)C→A (70)C→A (71)B→C (72)B→C (73)A→B (74)A→B (75)C→B (76)C→B (77)A→C (78)A→C (79)B→A (80)B→C (81)A→C (82)B→A (83)B→A (84)C→A (85)C→B (86)A→B (87)A→C (88)A→C (89)B→A (90)B→C (91)A→C (92)B→A (93)B→A (94)C→A (95)C→B (96)A→B (97)C→A (98)C→A (99)B→A (100)B→C (101)A→C (102)A→B (103)A→B (104)C→A (105)C→B (106)A→B (107)A→C (108)A→C (109)B→A (110)B→C (111)A→C (112)B→A (113)B→A (114)C→A (115)C→B (116)A→B (117)A→C (118)A→C (119)B→A (120)B→C (121)A→C (122)A→B (123)C→B (124)C→B (125)C→A (126)C→A (127)B→C (128)B→A (129)C→A (130)C→B (131)C→B (132)A→C (133)A→B (134)C→B (135)A→C (136)A→C (137)B→C (138)B→C (139)B→A (140)B→A (141)C→B (142)C→A (143)B→A (144)C→B (145)C→B (146)A→B (147)A→C (148)B→C (149)B→A (150)B→A (151)C→B (152)C→A (153)B→A (154)C→B (155)C→B (156)A→B (157)A→B (158)A→C (159)A→C (160)B→A (161)B→C (162)A→C (163)A→B (164)A→B (165)C→A (166)C→B (167)A→B (168)C→A (169)C→A (170)B→C (171)B→C (172)A→B (173)A→B (174)C→B (175)C→B
2,7,21,61,175,499(?),1419(?),
表を作って整理してみました。
手数が同じになる手順は規則性のある方を採用して、次の段に手を渡すようにしました。
| 1 | 2 | 3 | 4 | 5 | 6 | 計 | |
| 1 | 2 | 2 | |||||
| 2 | 5 | 2 | 7 | ||||
| 3 | 14 | 4 | 3 | 21 | |||
| 4 | 41 | 13 | 4 | 3 | 61 | ||
| 5 | 122 | 33 | 13 | 4 | 3 | 175 | |
| 6 | 365 | 81? | 33 | 13 | 4 | 3 | 499? |
最下段 2,5,14,41,122,365,
a(n)=3*a(n-1)-1
| a(n)= | 3n+1 2 |
その上の段が予想出来れば、仮説(?)は完成するのですが、、、。
別の角度からの推理。
変則ハノイの塔の三角形
| 0 | 2 | 7 | 21 | 61 | 175 | 499(?) | 1419(?) | |||||||
| 2 | 5 | 14 | 40 | 114 | 324 | 920 | ||||||||
| 3 | 9 | 26 | 74 | 210 | 596 | |||||||||
| 6 | 17 | 48 | 136 | 386 | ||||||||||
| 11 | 31 | 88 | 250 | |||||||||||
| 20 | 57 | 162 | ||||||||||||
| 37 | 105 | |||||||||||||
| 68 |
2,3,6,11,20,37,68,
a(1)=2,a(2)=3,a(3)=11
a(n)=a(n-1)+a(n-2)+a(n-3)
a(4)=6+3+2=11
a(5)=11+6+3=20
a(6)=20+11+6=37
a(7)=37+20+11=68
「変則ハノイの塔」の三角形には、トリボナッチ数列が関係しているのではないかと思います。
5,9,17,31,57,105,
a(1)=5,a(2)=9,a(3)=17
a(n)=a(n-1)+a(n-2)+a(n-2)
a(4)=17+9+5=31
a(5)=31+17+9=57
a(6)=57+31+17=105
14,26,48,88,162,
a(1)=14,a(2)=26,a(3)=48
a(4)=48+26+14=88
a(5)=88+48+26=162
こじつけの予想ですが、それらしく思えないでしょうか?。
【おまけ問題予想2】
前回の表で、条件を同じにして次の段に手を渡すことを厳守すれば、以下のようになり、この方がスッキリして、数学的帰納法の可能性が出てきます。
| 2 | |||||
| 5 | 2 | ||||
| 14 | 5 | 2 | |||
| 41 | 13 | 5 | 2 | ||
| 122 | 33 | 13 | 5 | 2 | |
| 365 | 81(?) | 33 | 13 | 5 | 2 |
2段目を、
2,5,13,33,81,
とすれば、
a(n)=n*2n-1+1 が予想されます。
トリボナッチの方は修正しなければなりませんが、基本は生かせるのでは、、、。
後は数学的証明が待たれます。
一般項の予想
| a(n)= | 3n+1 2 |
+ | n-1 Σ k=1 | (k*2k-1+1) ,a(1)=2,n≧2 |
2 ,7 ,21 ,61 ,175 ,499
1421 ,4057 ,11643 ,33631
トリボナッチ数列の規則性はなくなりましたが、この方がスッキリしていると思います。
Basicでのプログラムで確認するには時間的に困難です。
499までは正しいと思います。
一般項が整理出来ました。
| a(n)= | 3n+(n-2)*2n+2*n+1 2 |
,a(1)=2,n≧2 |
掲載されている手順と予想2の手順が異なっているので、
「同じ条件にして次の段に手を渡す」手順を送ります。
急がば回れ的手順が含まれます。
N=4
41 13 5 2
(1)A→C (2)A→B (3)C→B (4)C→A (5)B→A (6)C→B (7)A→C (8)A→B (9)C→B (10)C→A (11)B→A (12)B→C (13)A→C (14)B→A (15)B→A (16)C→A (17)C→A (18)C→B (19)A→C (20)A→C (21)A→B (22)A→B (23)C→A (24)C→B (25)A→B (26)A→C (27)A→C (28)B→A (29)B→C (30)A→C (31)B→A (32)B→A (33)C→A (34)C→B (35)A→B (36)A→C (37)A→C (38)B→A (39)B→C (40)A→C (41)A→B (42)C→A (43)C→A (44)C→B (45)C→B (46)A→C (47)A→C (48)B→A (49)B→A (50)C→B (51)C→A (52)B→A (53)C→B (54)C→B (55)A→B (56)A→C (57)B→C (58)A→B (59)A→B (60)C→B (61)C→BN=5
(1)A→C (2)A→B (3)C→B (4)C→A (5)B→A (6)C→B (7)A→C (8)A→B (9)C→B (10)A→C (11)B→A (12)B→C (13)A→C (14)B→A (15)B→A (16)C→A (17)C→A (18)C→B (19)C→B (20)A→C (21)A→B (22)C→B (23)A→C (24)A→C (25)B→C (26)B→A (27)C→A (28)C→B (29)C→B (30)A→C (31)A→B (32)C→B (33)C→A (34)B→A (35)B→C (36)A→C (37)B→A (38)B→A (39)C→A (40)C→B (41)A→B (42)A→C (43)A→C (44)B→A (45)B→C (46)A→C (47)B→A (48)B→A (49)C→B (50)C→B (51)C→A (52)C→A (53)B→C (54)B→A (55)C→A (56)C→B (57)A→B (58)A→B (59)A→C (60)A→C (61)B→A (62)B→C (63)A→C (64)A→B (65)A→B (66)C→A (67)C→B (68)A→B (69)C→A (70)C→A (71)B→C (72)B→C (73)A→B (74)A→B (75)C→B (76)C→B (77)A→C (78)A→C (79)B→A (80)B→C (81)A→C (82)B→A (83)B→A (84)C→A (85)C→B (86)A→B (87)A→C (88)A→C (89)B→A (90)B→C (91)A→C (92)B→A (93)B→A (94)C→A (95)C→B (96)A→B (97)C→A (98)C→A (99)B→A (100)B→C (101)A→C (102)A→B (103)A→B (104)C→A (105)C→B (106)A→B (107)A→C (108)A→C (109)B→A (110)B→C (111)A→C (112)B→A (113)B→A (114)C→A (115)C→B (116)A→B (117)A→C (118)A→C (119)B→A (120)B→C (121)A→C (122)A→B (123)C→B (124)C→B (125)C→A (126)C→A (127)B→C (128)B→A (129)C→A (130)C→B (131)C→B (132)A→C (133)A→B (134)C→B (135)A→C (136)A→C (137)B→C (138)B→C (139)B→A (140)B→A (141)C→B (142)C→A (143)B→A (144)C→B (145)C→B (146)A→B (147)A→C (148)B→C (149)B→A (150)B→A (151)C→B (152)C→A (153)B→A (154)C→B (155)C→B (156)A→C (157)A→C (158)A→B (159)A→B (160)C→A (161)C→A (162)B→C (163)B→C (164)A→B (165)A→C (166)B→C (167)A→B (168)A→B (169)C→B (170)C→A (171)B→A (172)C→B (173)C→B (174)A→B (175)A→B
◆解答Part2へ
(BasicとC++のプログラムがあります。)
◆宮城県 アンパンマン さんからの解答
【問題1】
19手
(1)A→B (2)C→B (3)A→C (4)B→C
(5)B→C (6)A→B (7)C→B (8)C→B
(9)C→A (10)C→A (11)B→A (12)B→A
(13)C→B (14)A→C (15)A→C (16)A→B
(17)A→B (18)C→B (19)C→B
【問題2】
44手
(1)A→C (2)A→B (3)C→A (4)C→A
(5)C→B (6)A→B (7)A→B (8)A→C
(9)B→A (10)B→A (11)B→C (12)B→C
(13)A→C (14)A→C (15)A→B (16)C→A
(17)C→A (18)C→B (19)C→B (20)A→B
(21)A→B (22)C→A (23)C→A (24)B→C
(25)B→C (26)B→A (27)B→A (28)C→A
(29)C→A (30)C→B (31)A→B (32)A→B
(33)A→C (34)A→C (35)B→C (36)B→C
(37)A→B (38)A→B (39)C→A (40)C→A
(41)C→B (42)C→B (43)A→B (44)A→B
【問題3】
96手
(1)A→B (2)C→B (3)A→C (4)B→C
(5)B→C (6)A→B (7)C→B (8)C→B
(9)C→A (10)C→A (11)B→A (12)B→A
(13)C→B (14)A→C (15)A→C (16)A→B
(17)A→B (18)C→B (19)C→B (20)A→C
(21)B→C (22)B→C (23)B→A (24)B→A
(25)C→A (26)C→A (27)B→C (28)B→C
(29)A→B (30)A→B (31)A→C (32)A→C
(33)B→C (34)B→C (35)A→B (36)C→B
(37)C→B (38)C→A (39)C→A (40)B→A
(41)B→A (42)C→B (43)C→B (44)A→C
(45)A→C (46)A→B (47)A→B (48)C→B
(49)C→B (50)C→A (51)C→A (52)B→A
(53)B→A (54)B→C (55)B→C (56)A→C
(57)A→C (58)B→A (59)B→A (60)C→B
(61)C→B (62)C→A (63)C→A (64)B→A
(65)B→A (66)C→B (67)A→C (68)A→C
(69)A→B (70)A→B (71)C→B (72)C→B
(73)A→C (74)A→C (75)B→A (76)B→A
(77)B→C (78)B→C (79)A→C (80)A→C
(81)A→B (82)A→B (83)C→B (84)C→B
(85)C→A (86)C→A (87)B→A (88)B→A
(89)C→B (90)C→B (91)A→C (92)A→C
(93)A→B (94)A→B (95)C→B (96)C→B
【問題4】
an=最短手数
a0=0,a1=2,
a2=7,a3=19,
a4=44,a5=96
Y=黄色、G=緑
A:
B:Y
C:G/YG/YG/.../YG
bn=最初の状態から上記の状態になる最短手数
an=bn-1+1+2n+1-3
an=bn-1+2n+1-2
bn=an-1+1+2(2n-1-1)
bn=an-1+2n-1
つまり
an=an-2+5*2n-1-3; n≧2
a2n=5(22n-1+22n-3+...+21)-3n+a0
a2n=10(4n-1)/3-3n; n≧0
a2n-1=5(22n-2+22n-4+...+22)-3(n-1)+a1
a2n-1=5(4n-1)/3-3n; n≧1
【おまけ】
an=色交互のときの最短手数
B1
A:Y/G/Y/G/Y/G/.../Y/G
B:
C:G/Y/G/Y/G/Y/.../G/Y
B2
A:Y
B:
C:G/YG/YG/YG/YG/.../YG
bn=B1からB2になる2n枚移動の最短手数
C1
A:
B:GY
C:YG/YG/YG/YG/YG/.../YG
C2
A:GY/GY/GY/.../GY
B:GY
C:YG
cn=C1からC2になる2n枚移動の最短手数
E1
A:Y/G/Y/G/Y/G/.../Y/G
B:
C:G/Y/G/Y/G/Y/.../G/Y
E2
A:Y/G
B:YG/YG/YG/YG/YG/YG/.../YG
C:G/Y
en=E1からE2になる2n枚移動の最短手数
F1
A:
B:GY
C:GY/GY/GY/GY/.../GY
F2
A:
B:GY/GY/GY/GY/GY/.../GY
C:
fn=F1からF2になる2n枚移動の最短手数
G1
A:
B:GY
C:YG/YG/YG/YG/.../YG
G2
A:
B:GY/GY/GY/GY/.../GY
C:
gn=G1からG2になる2n枚移動の最短手数
H1
A:
B:GY
C:GY/GY/GY/GY/GY/.../GY
H2
A:
B:GY/GY/GY/GY/GY/.../GY
C:GY
hn=H1からH2になる2n枚移動の最短手数
K1
A:
B:GY
C:YG/YG/YG/YG/.../YG
K2
A:
B:GY/GY/GY/GY/GY/.../GY
C:YG
kn=K1からK2になる2n枚移動の最短手数
P1
A:GY
B:YG
C:GY/GY/GY/.../GY
P2
A:GY/GY/GY/GY/.../GY
B:YG
C:
pn=P1からP2になる2n枚移動の最短手数
Q1
A:GY
B:YG
C:GY/GY/GY/.../GY
Q2
A:GY
B:YG/YG/YG/.../YG
C:
qn=Q1からQ2になる2n枚移動の最短手数
R1
A:GY
B:YG
C:GY/GY/GY/.../GY
R2
A:GY/GY/GY/.../GY
B:YG
C:GY
rn=R1からR2になる2n枚移動の最短手数
an=bn-1+1+cn-1+1+gn-1 1) bn=en-1+1+qn-1 2) en=bn-1+1+rn-1+1+rn-1 3) cn=kn-1+2+rn-1 4) fn=hn-1+2+cn-1+2+gn-1 5) gn=cn-1+2+fn-1 6) hn=hn-1+2+rn-1+2+fn-1 7) kn=cn-1+2+pn-1 8) pn=pn-1+2+cn-1+2+qn-1 9) qn=pn-1+2+kn-1 10) rn=rn-1+2+rn-1+2+rn-1=3rn-1+4 11) r0=0,r1=3より rn=5*3n-1-2; n≧14),8)より
9),10)より
pn=pn-1+cn-1+pn-2+6+kn-2 13)
4),12,13)より
kn+1-kn-1-rn-1-4 =kn-kn-2-rn-2-4+kn-2+2+rn-2+kn-1-kn-3-rn-3-4+6+kn-2 kn+1-kn-2kn-1-kn-2+kn-3 =4+40*3n-4 14)pn,qn,hn,cn も14)の漸化式を満たします。
x4-x3-2x2-x+1=0の解は
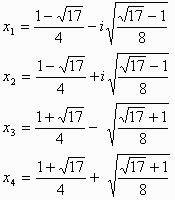
qn=A1*(x1)n+A2*(x2)n+A3*(x3)n+A4*(x4)n+(20/17)3n-4-2; n≧6 cn=B1*(x1)n+B2*(x2)n+B3*(x3)n+B4*(x4)n+(20/17)3n-4-2; n≧6 hn=C1*(x1)n+C2*(x2)n+C3*(x3)n+C4*(x4)n+(20/17)3n-4-2; n≧6qn,cn,hnの初値よりqn,cn,hnが決まります。
5),6)より
gn=gn-2+cn-1+cn-2+hn-2+6
| g2n= | n Σ i=4 | [c2i-1+c2i-2+h2i-2]+6(n-3)+g6; n≧4 |
| g2n-1= | n-1 Σ i=3 | [c2i+c2i-1+h2i-1]+6(n-3)+g5; n≧4 |
2),3)より
bn=bn-2+qn-1+2rn-2+3
bn=bn-2+qn-1+10*3n-3-1
| b2n= | n Σ i=4 | [q2i-1+10*32i-3]-n+4+b6 |
| b2n= | n Σ i=4 | [q2i-1]+5*35* | 32n-4-1
4 | -n+3+b6; n≧4 |
| b2n-1= | n Σ i=4 | [q2i-2+10*32i-4]-n+3+b5 |
| b2n-1= | n Σ i=4 | [q2i-1]+5*34* | 32n-4-1
4 | -n+3+b5; n≧4 |
1)よりanが得られます。
anの式は次のように表せます。
an=K1*(x1)n+K2*(x2)n+K3*(x3)n+K4*(x4)n+K5*(3)n+K6*(-1)n+K7*n+K8。K1,K2,...,K8はanの初値
◆愛知県 Y.M.Ojisan さんからの解答
チェックに用いたエクセルのマクロ move.xls だそうです。
実際に動きを確認できるので試してみてください。
【問題解答】
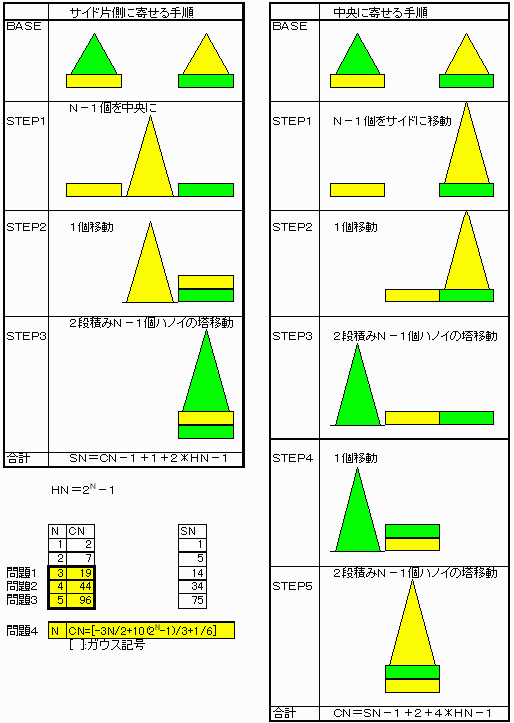
下図のように
中央に集める最小手数をCN、
サイドに集める最小手数をSN、
普通のハノイの塔の最小手数をHNとするとき、必然の手順は下図である。即ち
SN=CN-1+1+2×HN-1
CN=SN-1+2+4×HN-1
以上の漸化式にHN=2N−1 を代入して解くと
| CN= | 3N 2 | + | 10(2N−1) 3 | N:偶数 |
| CN= | 3N 2 | + | 10(2N−1) 3 | + | 1 6 | N:奇数 |
【おまけ解答】
色なしの上記手順において、2段積みハノイの塔の移動を除いては、色が重なる手順はない。
よって、色付2段積みハノイの手数を考える。
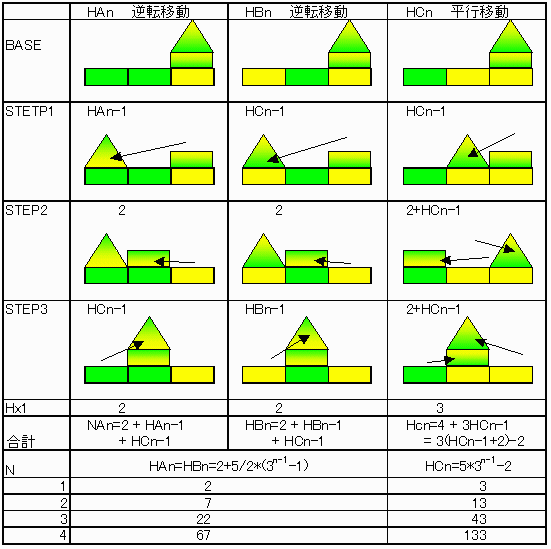
なお、上記手順表では2段積みのハノイの塔移動は色順を逆転(色が変わる)させる方法のみで示しているが、全部平行移動でも可能である。
しかし下図に示すように逆転移動の方が手順が少なく、得策ではない。
サイドに寄せる手順の場合、どちらのサイドに寄せるか選択の余地があり、常に逆転移動可能である。
一方中央に寄せる場合は、STEP2移動の移動元にまだ輪が残っている場合は、STEP3では平行移動のみ可能であり,
逆に残りが無い場合の最後のn=Nのときのみ逆転移動可能である。即ち
Sn=Cn-1+1+HAn-1
Cn=Sn-1+2+2×HAn-1 :n=N
Cn=Sn-1+2+2×HCn-1 :n<N
従っておまけの手順数は多くてもN>1に対し以下である。
なお、C1=2。
| CN= | 115×3N-2+12N+21 16 |
N:偶数 |
| CN= | 115×3N-2-12N+21 16 | + | 3 8 | N:奇数 |
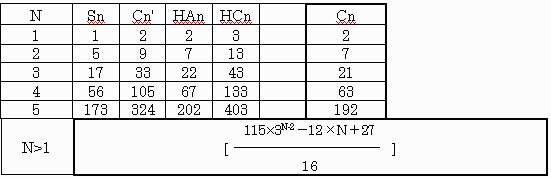
計算すると下表である。
奇数の式で切り捨てすれば偶数の値なのでガウス記号を使った。
最小かどうかは ?。
Cn'はn<NにおけるCnである。
◆ 解答Part2へ
◆ 問題へもどる
◆ 今週の問題へ