◆広島県 清川 育男 さんからの解答
プログラム(バックトラック)でのチェックでは今までの報告に間違いないです。
1→A、2→B、3→C を意味します。
●N=2 7手
1 - 3 1 - 2 3 - 1 3 - 1 3 - 2 1 - 2 1 - 2 3 - 1 3 - 2 1 - 3 1 - 3 1 - 2 3 - 2 3 - 2●N=3 21手
1 - 2 3 - 2 3 - 1 2 - 1 2 - 1 3 - 2 1 - 2 1 - 2 1 - 3 1 - 3 2 - 1 2 - 3 1 - 3 1 - 2 3 - 1 3 - 1 3 - 2 3 - 2 1 - 3 1 - 2 3 - 2 1 - 2 3 - 2 3 - 1 2 - 1 2 - 1 3 - 2 1 - 2 1 - 2 1 - 3 1 - 3 2 - 1 2 - 3 1 - 3 1 - 2 3 - 2 3 - 1 2 - 1 3 - 2 3 - 2 1 - 2 1 - 2 3 - 2 1 - 2 1 - 3 2 - 3 2 - 3 1 - 2 3 - 2 3 - 2 3 - 1 3 - 1 2 - 3 2 - 1 3 - 1 3 - 2 1 - 2 1 - 3 2 - 3 1 - 2 1 - 2 3 - 2 3 - 2 3 - 2 1 - 2 1 - 3 2 - 3 2 - 3 1 - 2 3 - 2 3 - 2 3 - 1 3 - 1 2 - 3 2 - 1 3 - 1 3 - 2 1 - 3 1 - 3 1 - 2 1 - 2 3 - 1 3 - 2 1 - 2●N=4 61手
1 - 3 1 - 2 3 - 2 3 - 1 2 - 1 3 - 2 1 - 3 1 - 2 3 - 2 3 - 1 2 - 1 2 - 3 1 - 3 2 - 1 2 - 1 3 - 1 3 - 1 3 - 2 1 - 2 1 - 3 2 - 3 1 - 2 1 - 2 3 - 2 3 - 2 1 - 3 1 - 3 2 - 1 2 - 3 1 - 3 2 - 1 2 - 1 3 - 1 3 - 2 1 - 2 1 - 3 1 - 3 2 - 1 2 - 3 1 - 3 1 - 2 3 - 1 3 - 1 3 - 2 3 - 2 1 - 3 1 - 3 2 - 1 2 - 1 3 - 2 3 - 1 2 - 1 3 - 2 3 - 2 1 - 2 1 - 3 2 - 3 1 - 2 1 - 2 3 - 2 3 - 2 1 - 3 1 - 2 3 - 2 3 - 1 2 - 1 3 - 2 1 - 3 1 - 2 3 - 2 3 - 1 2 - 1 2 - 3 1 - 3 2 - 1 2 - 1 3 - 1 3 - 1 3 - 2 1 - 2 1 - 3 2 - 3 1 - 2 1 - 2 3 - 2 3 - 2 1 - 3 1 - 3 2 - 1 2 - 3 1 - 3 2 - 1 2 - 1 3 - 1 3 - 2 1 - 2 1 - 3 1 - 3 2 - 1 2 - 3 1 - 3 1 - 2 3 - 1 3 - 1 3 - 2 3 - 2 1 - 3 1 - 3 2 - 1 2 - 1 3 - 2 3 - 1 2 - 1 3 - 2 3 - 2 1 - 3 1 - 3 1 - 2 1 - 2 3 - 1 3 - 2 1 - 2 1 - 3 1 - 2 3 - 2 3 - 1 2 - 1 3 - 2 1 - 3 1 - 2 3 - 2 3 - 1 2 - 1 2 - 3 1 - 3 2 - 1 2 - 1 3 - 1 3 - 1 3 - 2 1 - 2 1 - 3 2 - 3 1 - 2 1 - 2 3 - 2 3 - 2 1 - 3 1 - 3 2 - 1 2 - 3 1 - 3 2 - 1 2 - 1 3 - 1 3 - 2 1 - 2 1 - 3 1 - 3 2 - 1 2 - 3 1 - 3 1 - 2 3 - 2 3 - 2 3 - 1 3 - 1 2 - 3 2 - 1 3 - 1 3 - 2 3 - 2 1 - 3 1 - 2 3 - 2 1 - 3 1 - 3 2 - 1 2 - 1 3 - 2 3 - 2 1 - 2 1 - 2 1 - 3 1 - 2 3 - 2 3 - 1 2 - 1 3 - 2 1 - 3 1 - 2 3 - 2 3 - 1 2 - 1 2 - 3 1 - 3 2 - 1 2 - 1 3 - 1 3 - 1 3 - 2 1 - 3 1 - 3 1 - 2 1 - 2 3 - 1 3 - 2 1 - 2 1 - 3 1 - 3 2 - 1 2 - 3 1 - 3 2 - 1 2 - 1 3 - 1 3 - 2 1 - 2 1 - 3 1 - 3 2 - 1 2 - 3 1 - 3 1 - 2 3 - 1 3 - 1 3 - 2 3 - 2 1 - 3 1 - 3 2 - 1 2 - 1 3 - 2 3 - 1 2 - 1 3 - 2 3 - 2 1 - 2 1 - 3 2 - 3 1 - 2 1 - 2 3 - 2 3 - 2 1 - 3 1 - 2 3 - 2 3 - 1 2 - 1 3 - 2 1 - 3 1 - 2 3 - 2 3 - 1 2 - 1 2 - 3 1 - 3 2 - 1 2 - 1 3 - 1 3 - 1 3 - 2 1 - 3 1 - 3 1 - 2 1 - 2 3 - 1 3 - 2 1 - 2 1 - 3 1 - 3 2 - 1 2 - 3 1 - 3 2 - 1 2 - 1 3 - 1 3 - 2 1 - 2 1 - 3 1 - 3 2 - 1 2 - 3 1 - 3 1 - 2 3 - 1 3 - 1 3 - 2 3 - 2 1 - 3 1 - 3 2 - 1 2 - 1 3 - 2 3 - 1 2 - 1 3 - 2 3 - 2 1 - 3 1 - 3 1 - 2 1 - 2 3 - 1 3 - 2 1 - 2 1 - 3 1 - 2 3 - 2 3 - 1 2 - 1 3 - 2 1 - 3 1 - 2 3 - 2 3 - 1 2 - 1 2 - 3 1 - 3 2 - 1 2 - 1 3 - 1 3 - 1 3 - 2 1 - 3 1 - 3 1 - 2 1 - 2 3 - 1 3 - 2 1 - 2 1 - 3 1 - 3 2 - 1 2 - 3 1 - 3 2 - 1 2 - 1 3 - 1 3 - 2 1 - 2 1 - 3 1 - 3 2 - 1 2 - 3 1 - 3 1 - 2 3 - 2 3 - 2 3 - 1 3 - 1 2 - 3 2 - 1 3 - 1 3 - 2 3 - 2 1 - 3 1 - 2 3 - 2 1 - 3 1 - 3 2 - 1 2 - 1 3 - 2 3 - 2 1 - 2 1 - 2 3 - 1 3 - 2 1 - 2 1 - 3 2 - 3 1 - 2 3 - 1 3 - 2 1 - 2 1 - 3 2 - 3 2 - 1 3 - 1 2 - 3 2 - 3 1 - 3 1 - 3 1 - 2 3 - 1 3 - 1 3 - 2 3 - 2 1 - 3 1 - 2 3 - 2 3 - 1 3 - 1 2 - 3 2 - 1 3 - 1 2 - 3 2 - 3 1 - 3 1 - 2 3 - 2 3 - 1 3 - 1 2 - 3 2 - 1 3 - 1 3 - 2 1 - 2 1 - 2 1 - 3 1 - 3 2 - 1 2 - 3 1 - 3 1 - 2 1 - 2 3 - 1 3 - 2 1 - 2 3 - 1 3 - 1 2 - 3 2 - 3 1 - 2 1 - 2 3 - 2 3 - 2 3 - 1 3 - 2 1 - 2 1 - 3 2 - 3 1 - 2 3 - 1 3 - 2 1 - 2 1 - 3 2 - 3 2 - 1 3 - 1 2 - 3 2 - 3 1 - 3 1 - 3 1 - 2 3 - 1 3 - 1 3 - 2 3 - 2 1 - 3 1 - 2 3 - 2 3 - 1 3 - 1 2 - 3 2 - 1 3 - 1 2 - 3 2 - 3 1 - 3 1 - 2 3 - 2 3 - 1 3 - 1 2 - 3 2 - 1 3 - 1 3 - 2 1 - 3 1 - 3 1 - 2 1 - 2 3 - 1 3 - 1 2 - 3 2 - 3 1 - 2 1 - 3 2 - 3 1 - 2 1 - 2 3 - 1 3 - 1 3 - 2 3 - 2 1 - 3 1 - 2 3 - 2 3 - 1 3 - 2 1 - 2 1 - 3 2 - 3 1 - 2 3 - 1 3 - 2 1 - 2 1 - 3 2 - 3 2 - 1 3 - 1 2 - 3 2 - 3 1 - 3 1 - 3 1 - 2 3 - 1 3 - 1 3 - 2 3 - 2 1 - 3 1 - 2 3 - 2 3 - 1 3 - 1 2 - 3 2 - 1 3 - 1 2 - 3 2 - 3 1 - 3 1 - 2 3 - 2 3 - 1 3 - 1 2 - 3 2 - 1 3 - 1 3 - 2 1 - 3 1 - 3 1 - 2 1 - 2 3 - 1 3 - 1 2 - 3 2 - 3 1 - 2 1 - 3 2 - 3 1 - 2 1 - 2 3 - 2 3 - 1 2 - 1 3 - 2 3 - 2 1 - 2 1 - 2 3 - 1 3 - 2 1 - 2 1 - 3 2 - 3 1 - 2 3 - 1 3 - 2 1 - 2 1 - 3 2 - 3 2 - 1 3 - 1 2 - 3 2 - 3 1 - 3 1 - 3 1 - 2 3 - 2 3 - 1 2 - 1 3 - 2 3 - 2 1 - 2 1 - 2 3 - 1 3 - 1 2 - 3 2 - 1 3 - 1 2 - 3 2 - 3 1 - 3 1 - 2 3 - 2 3 - 1 3 - 1 2 - 3 2 - 1 3 - 1 3 - 2 1 - 2 1 - 2 1 - 3 1 - 3 2 - 1 2 - 3 1 - 3 1 - 2 1 - 2 3 - 1 3 - 2 1 - 2 3 - 1 3 - 1 2 - 3 2 - 3 1 - 2 1 - 2 3 - 2 3 - 2 3 - 1 3 - 2 1 - 2 1 - 3 2 - 3 1 - 2 3 - 1 3 - 2 1 - 2 1 - 3 2 - 3 2 - 1 3 - 1 2 - 3 2 - 3 1 - 3 1 - 3 1 - 2 3 - 2 3 - 1 2 - 1 3 - 2 3 - 2 1 - 2 1 - 2 3 - 1 3 - 1 2 - 3 2 - 1 3 - 1 2 - 3 2 - 3 1 - 3 1 - 2 3 - 2 3 - 1 3 - 1 2 - 3 2 - 1 3 - 1 3 - 2 1 - 3 1 - 3 1 - 2 1 - 2 3 - 1 3 - 1 2 - 3 2 - 3 1 - 2 1 - 3 2 - 3 1 - 2 1 - 2 3 - 1 3 - 1 3 - 2 3 - 2 1 - 3 1 - 2 3 - 2 3 - 1 3 - 2 1 - 2 1 - 3 2 - 3 1 - 2 3 - 1 3 - 2 1 - 2 1 - 3 2 - 3 2 - 1 3 - 1 2 - 3 2 - 3 1 - 3 1 - 3 1 - 2 3 - 2 3 - 1 2 - 1 3 - 2 3 - 2 1 - 2 1 - 2 3 - 1 3 - 1 2 - 3 2 - 1 3 - 1 2 - 3 2 - 3 1 - 3 1 - 2 3 - 2 3 - 1 3 - 1 2 - 3 2 - 1 3 - 1 3 - 2 1 - 3 1 - 3 1 - 2 1 - 2 3 - 1 3 - 1 2 - 3 2 - 3 1 - 2 1 - 3 2 - 3 1 - 2 1 - 2 3 - 2 3 - 1 2 - 1 3 - 2 3 - 2 1 - 2 1 - 2●N=5
| 3n+1 2 |
122手を前提にしてのその後 |
53手 計175手
1 - 2 1 - 2 1 - 3 1 - 3 2 - 1 2 - 3 1 - 3 1 - 2 1 - 2 3 - 1 3 - 2 1 - 2 3 - 1 3 - 1 2 - 1 2 - 1 2 - 3 2 - 3 1 - 2 1 - 3 2 - 3 1 - 2 1 - 2 3 - 2 3 - 1 2 - 1 2 - 3 2 - 3 1 - 2 1 - 3 2 - 3 1 - 2 1 - 2 3 - 1 3 - 1 3 - 2 3 - 2 1 - 3 1 - 3 2 - 1 2 - 1 3 - 2 3 - 1 2 - 1 3 - 2 3 - 2 1 - 2 1 - 3 2 - 3 1 - 2 1 - 2 3 - 2 3 - 2 1 - 2 1 - 2 1 - 3 1 - 3 2 - 1 2 - 3 1 - 3 1 - 2 1 - 2 3 - 1 3 - 2 1 - 2 3 - 1 3 - 1 2 - 1 2 - 1 2 - 3 2 - 3 1 - 2 1 - 3 2 - 3 1 - 2 1 - 2 3 - 2 3 - 1 2 - 1 2 - 3 2 - 3 1 - 2 1 - 3 2 - 3 1 - 2 1 - 2 3 - 1 3 - 1 3 - 2 3 - 2 1 - 3 1 - 3 2 - 1 2 - 1 3 - 2 3 - 1 2 - 1 3 - 2 3 - 2 1 - 3 1 - 3 1 - 2 1 - 2 3 - 1 3 - 2 1 - 2 1 - 2 1 - 2 1 - 3 1 - 3 2 - 1 2 - 3 1 - 3 1 - 2 1 - 2 3 - 1 3 - 2 1 - 2 3 - 1 3 - 1 2 - 1 2 - 1 2 - 3 2 - 3 1 - 2 1 - 3 2 - 3 1 - 2 1 - 2 3 - 2 3 - 1 2 - 1 2 - 3 2 - 3 1 - 2 1 - 3 2 - 3 1 - 2 1 - 2 3 - 2 3 - 2 3 - 1 3 - 1 2 - 3 2 - 1 3 - 1 3 - 2 3 - 2 1 - 3 1 - 2 3 - 2 1 - 3 1 - 3 2 - 1 2 - 1 3 - 2 3 - 2 1 - 2 1 - 2●N=6
365手を前提にその後の134手を確認できるか、
365手+81手とその後の53手。
ベーシック言語では時間的に無理です。
C言語等のコンパイル型言語なら十分に可能です。
最長手順の詰め将棋を解いていますから。
大分速くなりましたが、N=5は無理のようです。
N=2,3,4にセットしています。
変則ハノイの塔の解答プログラム (Basic)
◆愛知県 Y.M.Ojisan さんからのコメント
【清川育男さん解へのコメント】
(1)提示のBASICプログラムをほぼそのままC++で実行してみました。
(ファイル添付 7kB)
PIII/500MHzでのCPU時間は下表となりました。
CPUクロック当たりの性能はBASICとC++コンパイルで驚くほどは違わないだろうと思いますがどうでしょうか?。
この解法の場合、1.3倍/1手順 程度のE問題であることが、プログラムの配列Tを平均すると分かります。
従って、N=5のCPU時間はN=4のCPU時間の1.3175-61倍程度と推定され、下表のように、宇宙的時間が必要でC++コンパイルでも無理でしょう。
N=6の場合のあと134手の場合でも、推定525年で無理のようです。
| N | 2 | 3 | 4 | 5 |
| CPU時間 | 0.3m秒 | 5m秒 | 140秒 | 推定1700万年 |
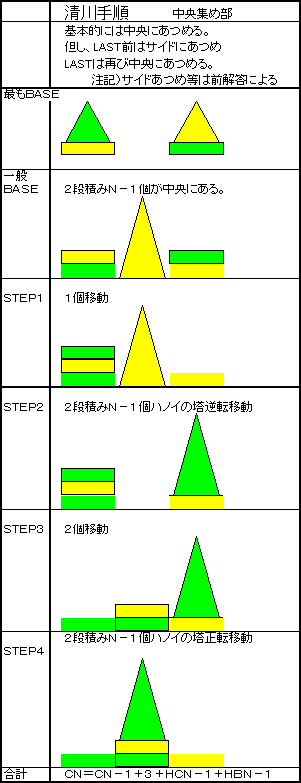
(2)清川育男さんが見つけないし最小を確認された 7,21,61,175の系列の手順を解析すると、一定の手順に従っていることが分かります。
手順を下図に示します。
この手順によるとN=6以上の解は清川予想より若干多めになります。
パソコン技で虱潰しに調べて見ると、
調べることができたN=8までは最小解になっていることがわかりました。
| N | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 清川手順 | 7 | 21 | 61 | 175 | 504 | 1472 | 4341 | 12899 | 38496 |
|
最小 (パソコン技) |
7 | 21 | 61 | 175 | 504 | 1472 | 4341 | − | − |
(3)パソコン技の方法
プログラムリストは分かりにくいので添付しませんが、原理は簡単です。
一度調べたことを全て記憶し、ループやその他無駄な手を再探索しないようにすれば、メモリー容量が許す範囲ではかなり早く探索ができます。
N=8の場合ハードディスクを用いた仮想メモリ(SWAP)まで動員していますが、それでも記憶しない方法よりは圧倒的に早いです。
それはこの問題の場合、記憶して無駄を省くと、探索すべき数が手順数に対して E問題ではなく、
P1問題の程度になってしまうからです。

◆広島県 清川 育男 さんからの質問
【Y.M.Ojisan さんからのコメントに対する質問】
縦型生成手続きによるアルゴリズムでは、過去の検索結果が利用されないので、 横型生成手続き(メモリー容量は多く必要とするが)によるアルゴリズムの方が速く検索されると言うことでしょうね。
確かに手順前後で、D手目の局面で同一局面となる可能性が考えられます。
そうなれば、横型生成手続きによるアルゴリズムでは過去の検索結果が利用されるので、その後の検索は省略出来ます。
したがって、横型生成手続きによるアルゴリズムの方が同一局面かどうかの照合に時間を要するが、その後の検索を繰り返す縦型生成手続きによるアルゴリズムより有利であると理解してよいのでしょうか。
横型生成手続きによるアルゴリズムを採用してみます。
これはと言う検索のための戦略があれば、、、。
◆愛知県 Y.M.Ojisan さんからのコメント
(1)
残念ながら/縦型生成手続/横型生成手続き/の定義を知りませんので確たる回答ができませんが、雰囲気的にはYESです。
(2)
照合・検索の時間をもったいなく思う気持ちはとても良く分かります。
しかし、問題にもよりますが、大抵の場合その先の何十万手の操作・探索に比べると、照合・検索の時間はゴミです。
ですから、よほど無駄のある方法で無ければ、戦略というほど凝らなくても十分な結果が得られます。
たとえばメモリー容量を優先するなら、可能性を否定できない状態に1対1対応の何らかのインデックスをつけ、インデックス順に一列に並べて、2分法を適用すれば十分です。
(3)
とはいえ、いろいろ小細工を弄したくなるのが人の常です。
特にこの変形ハノイの探索プログラムは小細工のため、今となっては作った本人すら何だったっけ状態です。
従って、他の方に解説なしで開示しても解読が困難と思いますが、とりあえず、ソース(13kB)だけ添付します。
次の土日に時間が有れば解説をつけようと思います。
(4)
なお、このプログラムの構造上の限界 NMAX=N=9で一晩かけて実行したところ答えに至り、清川手順の最小性がさらに確認されました。
HDが壊れるのではないと不安でしたが。
◆愛知県 Y.M.Ojisan さんからの解答
変形ハノイの塔探索プログラム解説
【ちょっと一般論】
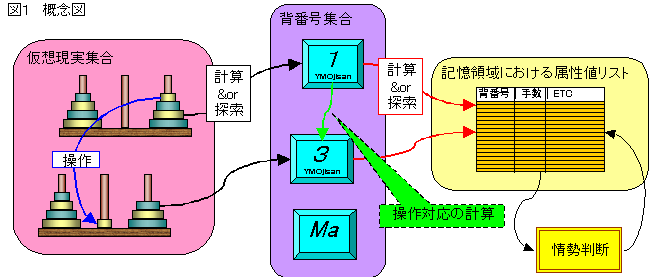
探索結果を記憶して虱潰しに探索するプログラムの一般的概念を図1に示す。
この場合の要点は
(1)仮想現実の状態に対して何らかの1対1対応の背番号つけること。
(2)その背番号を無駄なくかつ位置を探索しやすくメモリに割り付けること。
である。さらにできれば、
(3)仮想現実空間での操作(輪の移動)が、背番号集合の空間での計算で可能であること。
が探索速度向上の点から望ましい。
なお「情勢判断」とは最後まで探索する前に、明らかに探索しても無駄な探索枝をすてるような判断をすることである。
2/20版のソフトではこれを用いていませんが、今回の新バージョンではあとで紹介する1つの方法を追加しています。
【背番号付けの方法】
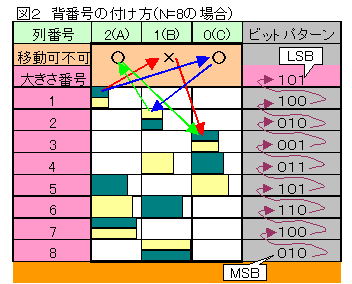
変形ハノイの塔の場合の背番号のつけ方を図2に示す。
色を無視したときの各大きさの輪の位置は図2の表で大きさ番号1〜6に示される6タイプがあり、これを図示のように各塔上の存在の有無に対応させた各々3bitのビットパターンで対応させるものとする。
色は手順を正しく行っている限り、交互にならぶので、一番上の状態だけ指定すればよい。
各塔毎に(青・黄・空白)の3色があるが、全部が同色である場合はない。
即ち3×3×3−3=24通り有る。
さらに青と黄を交換しても手順数に影響はない。
よって実質12とおりに番号付けを行えばよい。
このうち空白は輪の状態から規定可能なので、4bitは不要で、実際には図3に示すように4通りを区別すればよいが、操作する時の容易性から3bitとする。
この1bitの無駄は【メモリーの圧縮】で確実に取り戻せる。
その3bitは色そのものではなく、塔間の移動の可不可を示すようにつける。
すなわち塔の番号を0〜2とするときm番の塔とn番の塔間の移動の可不可を
3−m−n番の塔の位置につける。
このようにしてつけたビットパターンを図1の紫矢印で示すようにつないで2進法とみなして背番号とする。
N=8の場合は27ビットの整数となる。
背番号の範囲は、仮想現実で存在しうる状態数に比較し、かなり多いものとなるが、各大きさの輪の状態が分離しているので、
操作=計算を背番号集合上で実施するのに便利なのである。

【背番号集合上での操作】
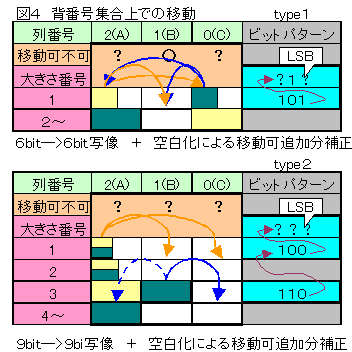
輪の移動の選択枝はまず最初に、最も小さい輪の状態(3bit)と移動可不可の状態(3bit)で決まる。
そしてそれらは、図4に示すように小さな輪が2箇所にある場合(type1)と1箇所にある場合(type2)に分かれる。
(type1)の場合は移動はすべて最も小さい輪の移動だけの最大4通りがあるが、その結果影響を受けるのは、やはり最も小さい輪の状態(3bit)と移動可不可の状態(3bit)の合計6bitのみである。
一方(type2)の場合は最も小さい輪の移動の最大2通りに加え、次に高い位置にある輪の移動(最大2通り)が選択肢となる。
この場合影響を受けるのは関連の9bitのみである。
因みに次に高い輪の探索は、背番号を3bitずつずらしては小さい輪のある位置をマスク( 背番号bitshift bitAnd 101 等)して0か0でないか判定する。
6bitは64 9bitは512であり、大した量ではないので計算時間短縮のために、全てのケースについて移動後の状態を配列に記憶させ、ビット毎の排他論理輪で背番号に対して操作(ビット計算)ができるようにしてある。
ただし、移動の結果、ある塔が空白になった場合のケースに関しては、別途空白状態を検査し、空白の塔があれば、対応する移動可不可ビットパターンの3bitを修正する。
因みに空白かどうかの検査は 001001001・・・という各塔対応のビットパターンと移動後の背番号とのbitAndをとれば一発で検査可能である。
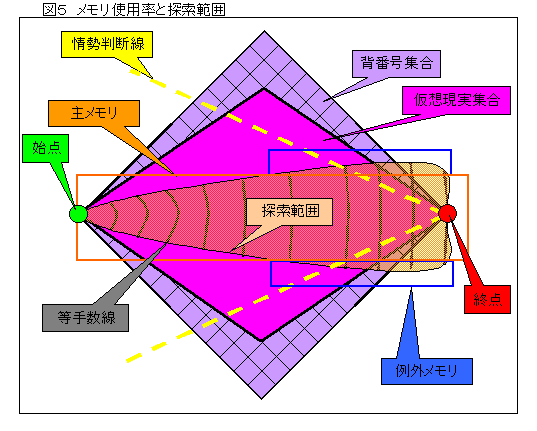
【メモリーの圧縮概念】
図5にこの問題のメモリーの利用状態を示す。
仮想現実に対して背番号は過大に割り当てていることは先に述べたとおりである。
さらに、この問題では探索する範囲は、手順が進んでも以外に増えないため(P問題程度)、最小手順を発見するのまでに利用される個数は相対的に非常に少なく、背番号は大部分が使われることなく終了する。
背番号からメモリー位置を探索するオーバーヘッドを小さくするには
メモリーアドレス=背番号×定数とするのが良いが膨大な無駄メモリーが必要になるのである。
そこで、一つのメモリーグループ(たとえば要素数32個)を1つの背番号グループ(たとえば要素数4096)に割り当て、探索で出てきたもの順にメモリーに記録してゆくことにする。
即ち図の主メモリー部分である。
このようにすれば当然メモリーは減少します。
また、32個ぐらいであれば、再度アクセスするときに端から順次全部照合していても時間はかかりません。
問題は32個で納まるかと言うことです。
そこで32個でおさまらない例外的な場合に備えて、全部まとめてた例外メモリを容易しておき、ここに全部入れてしまいます。
【メモリーの圧縮詳細】
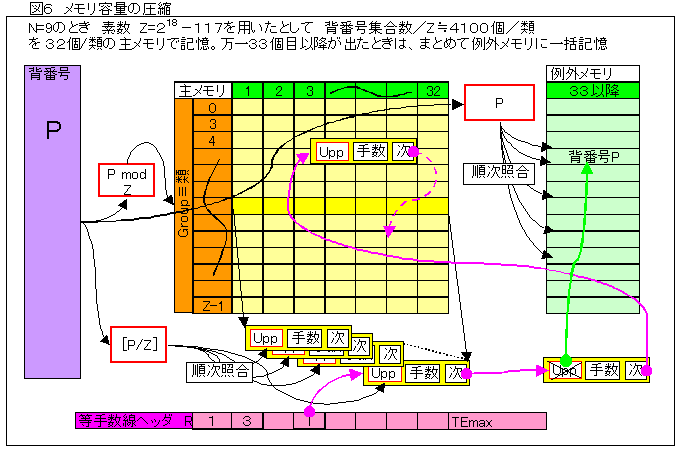
図6にこのプログラムのメモリー割付の方法の詳細を示します。
2のべき乗値から1%ぐらい小さい素数Zを用いて背番号の集合をmod ZでZ個の類に分け、これに少数(32個)のメモリーを対応させています。
メモリーの属性値(手順数)がどの背番号のものか照合するために各メモリーには
[背番号/Z]の値を2バイト整数で記録しておきます。
例外が出た場合は例外メモリの方に入れますが、再アクセス時の背番号照合のために、背番号をそのまま記憶する領域を別途設置してあります。
【探索方法】
最初の状態から初めて、1手で到達するもののリスト、2手で到達するもののリスト、。。。。と言う風に順次探索してリストを作って行きます。
つまり、メモリー空間上に手順数の等高線を低い方から書いて行く感じです。
図5参照。
そして最終状態の背番号に達したら、終了です。
これで最小手順数がきまります。
実際の手順は、最終状態から逆にたどって、初期状態にたどり着くことで再現することができます。
なお、等手順数(手数T)の背番号のリストは各背番号のメモリーに用意されたリンク(次)により、等手数線ヘッダR[T]から繋がっています。
図6参照。
【情勢判断の例】
2/20のプログラムでは「情勢判断」は入れていませんでした。
それはこの問題の場合、前にも申しましたが探索範囲があまり広がらないので、効果が少ないと考えられるからです。
(注:手数に対しE(指数的増加)問題の場合は効果絶大)
しかし実際に下記の方法を加えてみると予想外の効果がありました。
即ち例外メモリが殆ど使われなくなったのです。
このため2/20ソフトに比べ、さらにメモリーが圧縮可能となり、
N=9まで全部RAM(私のPCは128MB)上で計算できるので、圧倒的に早くなりました。
HDアクセスのため1晩(実際は2時間)かかっていたのが10秒程度になってしまいました。
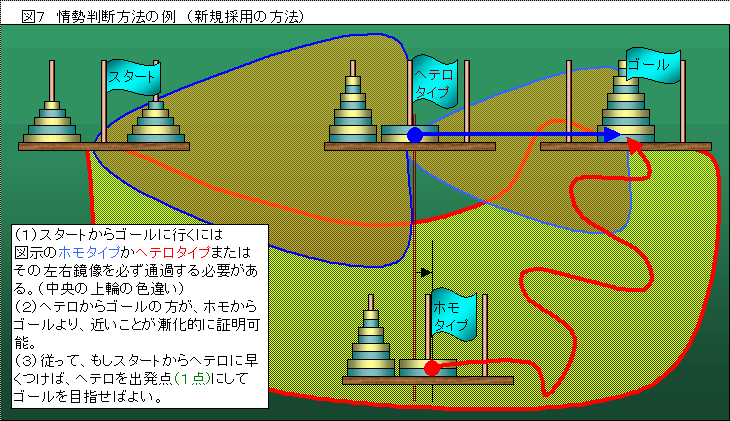
方法は下図に示すとおりです。
必ず通らなければならないパターン(ホモタイプ、ヘテロタイプ)に着目し、ヘテロタイプからゴールの方がホモタイプからゴールより近い(漸化的に証明可能だがここでは省略)ので、もし初期状態からの探索でヘテロに早く到着すれば、広がった探索範囲を一旦1点に絞りこみ探索時間を短縮できます。
清川手順はヘテロ通過ですからこの賭けは勝算があり、実際N=9までは成功しています。
【新プログラム】
情勢判断を追加し、メモリ関係パラメータを調整したソフト17kBを添付します。
なお、公開用に不要な変数などを削除・整理し、変数名を長くかつ統一し、少し解読しやすくしたつもりです。
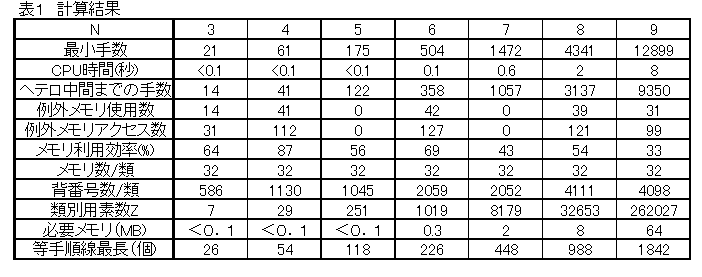
【計算結果】
下表参照。PIII/500MHz/128MB仕様
【P.S.】
CPU時間的にはまだまだ計算できそうです。
CPU時間は6Nに比例すると予測されるからです。
問題はメモリですが、あと4分の1にはできるでしょう。
総合するとこの方法では、N=10までは確実だがN=11はメモリ限界でできなさそうです。
◆広島県 清川 育男 さんからのコメント
「変形ハノイの塔」N=5 Y.M.Ojisan さん の解答が正しいことを確認できました。
中間点のヘテロ通過のその中間点も1つの関門になりますが、そこまでの手数が判れば総手数が解る漸化式を見つけました。
N=10 の結果が知りたいです。
◆ 解答Part1へ
◆ 問題へもどる
◆ 今週の問題へ