『今週の問題』第109回　解答

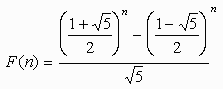
【コメント】

おまけの問題はいくつかの解はわかりましたが一般的には解けていません。
継続して解答を募集します。

それにしてもシドニー数列という名称は今の季節にぴったりですね。
ちなみにおまけの問題の考案者はフィボナッチであり、この問題はフィボナッチつながりで出題しました。

◆東京都の中学校１年生　ゴンザレス田中 さんからの解答

１段目の数字をａとし、 ２段目の数字をｂとすると
下の表のように １７段目の数字は
６１０ａ＋９８７ｂになる。

また、６１０ａ＋９８７ｂ＝１０×（６１ａ＋９８ｂ）＋７ｂ

になるから、 １７段目の１けたの数字は、７ｂになる。
つまり、１段目がどんな数字であっても、１７段目は、２段目の数字の７倍になるのである。

１段め ａ 
２段め ｂ 
３段め ａ＋ｂ 
４段め ａ＋２ｂ 
５段め ２ａ＋３ｂ 
６段め ３ａ＋５ｂ 
７段め ５ａ＋８ｂ 
８段め ８ａ＋１３ｂ 
９段め １３ａ＋２１ｂ 
１０段め ２１ａ＋３４ｂ 
１１段め ３４ａ＋５５ｂ 
１２段め ５５ａ＋８９ｂ 
１３段め ８９ａ＋１４４ｂ 
１４段め １４４ａ＋２３３ｂ 
１５段め ２３３ａ＋３７７ｂ 
１６段め ３７７ａ＋６１０ｂ 
１７段め ６１０ａ＋９８７ｂ 

◆石川県の高校生　むろ さんからの解答

【問題１−１】

５

【問題１−２】

全て５

【問題２−１】

８のとき６
３のとき１
７のとき９
０のとき０

【問題２−２】

◆シドニー数列 シドニー数列とは　フィボナッチの数列のような感覚で １つ前と２つ前の項の数の和の１の位に着目した数列。 初項６　第２項９　なら ６＋９＝１５≡５　（mod１０）となり第３項は５である。

「１」
１，１，２，３，５，８，３，１，４，５，９，４，３，７，０，
７，７，４，１，５，６，１，７，８，５，３，８，１，９，０、
９，９，８，７，５，２，７，９，６，５，１，６，７，３，０、
３，３，６，９，５，４，９，３，２，５，７，２，９，１，０、
１，１，２，、、、、、、、、、、（繰り返し）

「２」
２，２，４，６，０，６，６，２，８，０，８，８，６，４，０，
４，４，８，２，０，２，２，、、、、、

「３」
１，３，４，７，１，８，９，７，６，３，９，２，１，３，、、、

「４」
８，４，２，６，８，４，、、、、

「５」
５，０，５，５，０，、、、、

「６」
０，０，０，、、、、

（性質）

１ならば７，
２ならば４，
３ならば１，
４ならば８，
５ならば５，
６ならば２，
７ならば９，
８ならば６，
９ならば３，
０ならば０　　となる。

また全ての組を合わせると、０から９の１０個の数から２つ選んで並べる順列の組を全部取り尽くしている。
問題の１段目と２段目はこの２つを選ぶ作業だから、題意を満たす全ての組を取り尽くしている。

つまり問題の２段目と１５段目の関係は上の（性質）の通りである。

【感想】

数ヶ月前に　この数列のことを知りましたが、まさかこんなところで役に立つとはおもわなかったので、 ちょっとビックリです
　、、、、。（＾＾）

◆兵庫県の高校生　オイラーの弟子のいとこ さんからの解答

【問題１−１】

０のとき・・・５
１のとき・・・５
２のとき・・・５
３のとき・・・５
４のとき・・・５
５のとき・・・５
６のとき・・・５
７のとき・・・５
８のとき・・・５
９のとき・・・５

【問題１−２】

すべて５になってますね

[ここまでの感想]

ここまでやっててっきり１７段目の数は２段目の数と同じになると思ってしまいましたよ
でも・・・

【問題２−１】

８のとき・・・６
３のとき・・・１
７のとき・・・９
０のとき・・・０

【問題２−２】

結論：１７段目の数は２段目の数に７をかけたものの１の位の数である

証明：
本当は一の位だけ持ってくるのですがあとで引いても差し支えがないので最後にまとめて引きます
１段目の数をa,２段目の数をbとすると１７段目までの数は以下のように表せます

１段目の数       a
２段目の数       b
３段目の数      a+b 
４段目の数      a+2b
５段目の数      2a+3b
６段目の数      3a+5b
７段目の数      5a+8b
８段目の数      8a+13b
９段目の数      13a+21b
１０段目の数    21a+34b
１１段目の数    34a+55b
１２段目の数　　55a+89b
１３段目の数    89a+144b
１４段目の数    144a+233b
１５段目の数    233a+377b
１６段目の数    377a+610b
１７段目の数    610a+987b

ところで610aの一の位の数はaの値にかかわらず０となる
（なぜなら610a＝600a+10a+0a）

よって１７段目の数は987ｂの一の位の数となる

また987b＝900b+80b+7bより
987bの一の位の数＝7bの一の位の数　となる

ところでbは２段目の数だから１７段目の数は２段目の数に７をかけたものの１の位の数である

[感想]

一問目だけやると本質が見えないっていうのはやっぱり数学ですね

◆広島県　清川　育男 さんからの解答

【前提】

フィボナッチ数列が関係しています。

1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987

A(17)=610*A(1)+987*A(2)
A(17)≡7*A(2) (mod 10) ......(1)

【問題１−１】

A(2)=5

(1) より
A(17)=7*5≡5 (mod 10)

したがって、
A(1)=0,1,2,3,4,5,6,7,8,9

いずれの場合も１７段目は５。

【問題１−２】

すべて、５。

【問題２−１】

A(2)=8

(1) より
A(17)=7*8≡6 (mod 10)

したがって、
A(1)=0,1,2,3,4,5,6,7,8,9

いずれの場合も１７段目は６。

A(2)=3

(1) より
A(17)=7*3≡1 (mod 10)

したがって、
A(1)=0,1,2,3,4,5,6,7,8,9

いずれの場合も１７段目は１。

A(2)=7

(1) より
A(17)=7*7≡9 (mod 10)

したがって、
A(1)=0,1,2,3,4,5,6,7,8,9

いずれの場合も１７段目は９。

A(2)=0

(1) より
A(17)=7*0≡0 (mod 10)

したがって、
A(1)=0,1,2,3,4,5,6,7,8,9

いずれの場合も１７段目は０。

【おまけ】

b,c,d,e,f,g は自然数で、(b,c)=1,e>d,f>g とする。

a =

(

b c

)

2

，a-5=

(

d c

)

2

，a+5=

(

e c

)

2

と表わせると仮定する。

b²-5c²=d²
b²+5c²=e²

b2=

d2+e2 2

c2=

e2-d2 10

d+e=f，e-d=g　とおく。

e=

f+g 2

(1)

d=

f-g 2

(2)

b2=

f2+g2 4

(3)

c2=

f*g 10

(4)

(1),(2),(3),(4) より、f,gは偶数でなければならない。

f,gがピタゴラス数であるとすれば、f*g は １２の倍数でなければならない。
＊＊＊（「今週の問題」にありました。）

(4)より、
f*g=12*12*10 とすると、c=12

f*g=12*12*10=1440

(f,g)=(2,720),(4,360),(6,240),(8,180),
(10,144),(12,120),(16,90),(18,80),
(20,72),(24,60),(30,48),(32,45),(36,40)

ピタゴラス数を満たすのは、
f=18,g=80
18²+80²=82²

(1)より e=49
(2)より d=31
(3)より b=41

a =

(

41 12

)

2

a+5=

(

49 12

)

2

、a-5=

(

31 12

)

2

は条件を満たす。

kを自然数とする。

a =

(

41k 12k

)

2

も条件を満たす。

a

(

41 12

)

2

41は素数，

(

3344161 1494696

)

2

3344161は素数

a-5

(

31 12

)

2

31は素数，

(

113279 1494696

)

2

113279は素数

a+5

(

49 12

)

2

49=72，

(

4728001 1494696

)

2

4728001は素数

12=(2²)*3　1494696=(2³)*3*(7²)*31*41

分母に 2*3*(7²)*31*41 と前の素因数が現れるのは偶然ではないのでしょうね。
一般解が楽しみです。

◆宮城県　アンパンマン さんからの解答

【問題１−１】

5

【問題１−２】

必ず5になります。

【問題２−１】

6,1,9,0

【問題２−２】

1段目をa,2段目をbとします。

x_i=x_i-1+x_i-2, x₁=a,x₂=bとすると x_n=f_n-2 a+f_n-1 b。
(f_iはフィボナッチ数、f₁=f₂=1)

ゆえに
ｙ_n＝7段目≡f_n-2 a+f_n-1 b (mod 10), 0≦y_n≦9

x₁₇=610a+987bより
ｙ₁₇≡7b (mod 10), 0≦y₁₇≦9

b＝５の場合、y₁₇=5

ちなみにx₇=5a+8b, x₁₂=55a+89bより
(y₇,y₁₂)=(0,5)、(5,0) (aは偶数、奇数によります）

ｙ₁₇≡7b (mod 10), 0≦y₁₇≦9 より

b=8 → ｙ₁₇= 6
b=3 → ｙ₁₇= 1
b=7 → ｙ₁₇= 9
b=0 → ｙ₁₇= 0

【おまけ】

a =

p2 q2

, 題意より

p²+5q²=r²,
p²-5q²=s²
(p,q,r,sは整数, (p,q)=1）

10q²=r²-s²=(r-s)(r+s)

(p,q)=1 と((r²,s²)≦(2p²,10q²)より

(r²,s²)=1 (2は有り得ない）

r-s,r+s両方偶数か奇数 と0≦s＜r より qは偶数。

q=2mn　((m,n)=1)とすると

Case1:

r-s=2n²,　r+s=20m²,
r=10m²+n²,
s=10m²-n²
↓
p²=100m⁴+n⁴

10m²=2uv, n²=u²-v²
↓

u =

g2+h2 2

, v=

g2-h2 2

, n=gh

↓
g⁴-h⁴=20m²

g=3,h=1,m=2,n=3, p=41,q=12,

a =

(

41 12

)

2

Case2:

r-s=4n²,　r+s=10m²
↓
r=5m²+2n², s=5m²-2n²
↓
p²=25m⁴+4n⁴

p =

u2+v2 4

,2n2=

uv 2

,5m2=

u2-v2 4

↓
u=g², v=h²
↓
g⁴-h⁴=20m²

(上と同じ、g=3,h=1,m=2)

u=9, v=1, m=2,n=3,p=41,q=12

a =

(

41 12

)

2

a+5=

(

49 12

)

2

、a-5=

(

31 12

)

2

◆福岡県　古豚 さんからの解答

【問題１−１】

5

【問題１−２】

1段目の数がどんな数でも、17段目は　 5

【問題２−１】

2段目の数が　8のとき　17段目の数は　6
2段目の数が　3のとき　17段目の数は　1
2段目の数が　7のとき　17段目の数は　9　
2段目の数が　8のとき　17段目の数は　0

17段目の数は、2段目の数を7倍したときの1の位の数

【おまけ】

a =

1050625 90000

=

(

1025 300

)

2

a+5=

1500625 90000

=

(

1225 300

)

2

a-5=

600625 90000

=

(

775 300

)

2

問題1、2は10の位を省略しないで足し算をすると、1段目の数をa、2段目の数をｂ

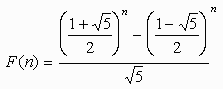
とすると、

ｎ段目の数は　F(n-２)×a+F(n-1)×ｂ
17段目の数は　610a+987bとなります。
（係数はフィボナッチの数列）

◆愛知県　Y.M.Ojisan さんからの解答

【問題１−１】

全部５

【問題１−２】

１７段目の数は１段目によらない。

【問題２−２】

６　１　９　０

【問題２−２】

１７段目の数＝２段目×７　の１の位。

１７段目の数
=N1×(1段=1 &  2段=0のときの17段目の数)＋ N2×(1段=0 &  2段=1のときの17段目の数) mod 10　
=N1×0＋N2×7　mod 10
=N2×7　mod 10

【おまけ】

a =

(

41 12

)

2

問題を定式化すると、以下を満たす整数Ａ，Ｂ，Ｃ，Ｄを見つけることである。

Ａ²＝Ｂ²−５Ｄ²＝Ｃ²＋５Ｄ² ------(1)

この時　a =

(

Ａ Ｄ

)

2

-------(2)

(1)より
（Ｂ−Ｃ）（Ｂ＋Ｃ）＝１０Ｄ²

Ｄ＝xyz とすると以下の２ケースが考えられる。
ただしx,y,zは互いに素な整数。

(A) Ｂ−Ｃ＝２x²z & Ｂ＋Ｃ＝5y²z
(B) Ｂ−Ｃ＝x²z & Ｂ＋Ｃ＝5*2y²z

途中省略するが(A)(B)いずれの場合も最終的に

γ²＝（α'²）²＋（１０β²）²　 -------(3)

にまとめられる。

さらに３による剰余を検討すると

γ²＝（９α²）²＋（１０β²）²　 -------(4)

を満足する整数α、β、γが存在するとき(1)を満たす整数があって、

a =

(

γ ６αβ

)

2

であることに至る。ちなみに

a±5 の分子
={（９α2）2＋（１０β2）2±180α2β2}
＝（ ９α2±１０β2）2

よって　a =

(

41 12

)

2

である。

因みに a+5=

(

49 12

)

2

、a-5=

(

31 12

)

2

【Ｐ．Ｓ．】

α、β≦２０では約分後
　41/12　以外の答えはない。

◆愛知県　Y.M.Ojisan さんからの解答(その２)

【おまけ】

ａ＞５　であるので、

ａ＝Ｘ2＋

(

５ ２Ｘ

)

2

(≧５) とおけば

ａ±５＝（Ｘ±

５ ２Ｘ

)

2

であるので、

Ｘが有理数ならａ±５は有理数の平方数である。

ａが有理数Ｙの平方数であるとする。結局

曲線：Ｙ2＝Ｘ2＋

(

５ ２Ｘ

)

2

の有理点を探す問題になる．

さらに変形すると下記のピタゴラス定理の有理点であることが必要条件である。

曲線：１＝α²＋β²

ここで　α＝

Ｘ Ｙ

，β＝

５ ２ＸＹ

α、βは有理数パラメータｔを媒介として下記式で表せる．

α＝

ｔ2−１ ｔ2＋１

，β＝

２ｔ ｔ2＋１

以上から

Ｘ2＝

５α ２β

＝

５（ｔ2−１） ４ｔ

両辺に （２*5ｔ）²を掛けると

(２＊５＊Ｘ＊ｔ)²＝(５ｔ)³−２５(５ｔ)であるので　
10Xt=y 5t=xと置けば

楕円曲線：y²＝x³−25x＝x(x-5)(x+5)
の有理点を探す問題になる。

(0,0) (5,0)(-5,0)(-4,6) (25/4,75/8)。。。。

以下教科書抜粋

楕円曲線　ｙ²＝ｘ³＋ａｘ＋ｂ　上の
２点、p₁(x₁,y₁)、p₂(x₂,y₂)に対して、
点p₃(x₃,y₃)を対応させる演算を、以下のように定義する。

• x₁≠x₂のとき、
  

  λ＝

  y2−y1 x2−x1

  ，ν＝

  y1x2−y2x1 x2−x1

• x₁＝x₂、y₁＝y₂≠０のとき、
  

  λ＝

  3x12＋ａ 2y1

  ，ν＝

  −x13＋ａx1＋2ｂ 2y1

x₃＝λ²−x₁−x₂
y₃＝−λx₃−ν

この演算によって、楕円曲線上の点は、群となり、かつ、この演算は可換（交換可能）なので、楕円曲線上の点は、この演算により加法群をなす。

以上の式で計算した　√aを下記に示します。
有限個数なのか無限なのか分かりませんが、これ以降を浮動小数点で計算したところまだありそうです。

41 12

，

3344161 1494696

，

654686219104361 178761481355556

160443526614433014168714029147613242401001 50016678000996026579336936742637753055940

。。。。。。。。。。　　　　　

　◆　問題へもどる

　◆　今週の問題へ

数学の部屋へもどる