『今週の問題』第108回　解答

【コメント】

この問題は奇数は全て先手必勝。
Y.M.Ojisanさんからのご指摘により，偶数での後手勝ちは
4,8,14,20,24,28,34,38,42,54,58,62・・・？
ではないかと思われますが，いまだ未解決です。
継続して解答を募集します。

◆東京都　ぱずきち さんからの解答(NEW!!)

必勝法はもうすこし時間がかかりそうなので，任意のパターンに対する判定法まで にしました。

　この問題は以前TV番組のなかで出てきたので考えたことがあります。
ある程度プログラムによる力まかせの方法を用いましたが，その結果をもとに考察した結果，非常に興味深い知見が得られました。
そして，ある数（現在２０４）以下の数の組み合わせからなる任意の状態に対して，比較的容易に先手必勝か後手必勝かを判定できる方法を見つけましたので，紹介いたします。

もう少し考察すれば，必勝法も得られるかもしれません。

１．準備

定義１.　状態（パターン）の表しかた

直線上に碁石を置いて行くと，碁石がおける領域が分断されていきます。
こうして碁石を置いていった途中の状態は，残った連続領域（個数Ｒ）の長さ
ｎ1，ｎ2，．．．ｎrにより決まるパターンで表すことができます。

よって状態Ａまたはそのパターンを
Ａ＝{ｎ1，ｎ2，．．．ｎr}で表します。

　状態Ａの性質はｎ1，ｎ2，．．．ｎrの順序に依りませんので
{ｎ1，ｎ2，．．．ｎr}は集合に近いのですが，同じ値の要素を持つことができる点が異なります。

　また，パターンＡが２つの部分パターンＢ，Ｃに分けることができる場合，すなわち
Ｂ＝{ｎb1，ｎb2，．．．ｎbr}，
Ｃ＝{ｎc1，ｎc2，．．．ｎcs}，
Ａ＝{ｎb1，ｎb2，．．．ｎbr，ｎc1，ｎc2，．．．ｎcs}の時，
Ａ＝Ｂ＋Ｃで表します。

　この定義からパターンの要素ｎ1〜ｎrは本来自然数であるべきで，置く場所がない状態は空集合に相当する{　}で表されるべきです。

　しかし，要素として０や−１を許し，その領域には碁石を置けないとすると後の記述が簡単化されるので，形式的にそうします。

　そうすると，１つの状態に対応するパターンが一意に定まらなくなりますが，余り問題にはなりません。

定義２.　判定関数

パターンＡが先手必勝か後手必勝かを表す関数ｆ(Ａ)を次のように定義します。

　ｆ(Ａ)＝０           （Ａが後手必勝の時）
　ｆ(Ａ)＝１           （Ａが先手必勝の時）　
　ｆ({ })＝ｆ({０})＝ｆ({−１})＝０　（便宜上）
命題１.　判定関数の性質１
（１．１）　ｆ(Ａ＋Ａ)＝０　　　　　　　　　　　　（まね碁）
（１．２）　ｆ(Ａ)＝０ならばｆ(Ａ＋Ｂ)＝ｆ(Ｂ)
　　　　　　　　　　　　　　（後手必勝のパターンは除去可能）
（１．３）　ｆ(Ａ＋Ｂ)＝０，ｆ(Ｂ＋Ｃ)＝０ならば，
　　　　　　ｆ(Ａ＋Ｃ)＝０　　　　　　　　　　　　（推移律）
（１．４）　ｆ({２ｎ＋１})＝１
証明（説明）

（１．１）後手は先手のまねをする事で必ず勝つことができるので。

（１．２）
もし，ｆ(Ｂ)＝０ならば，もし先手が部分Ａに置いたら後手はＡの後手必勝手順を，先手が部分Ｂに置いたら後手はＢの後手必勝手順を進めることで，必ず後手が勝つことができる。

もし，ｆ(Ｂ)＝１ならば，先手はＢの先手必勝手順の１手目に置くことで
ｆ(Ａ)＝０，ｆ(Ｂ’)＝０として，後手に手番を渡すことができるので先手必勝である。

以上よりｆ(Ａ)＝０ならばｆ(Ａ＋Ｂ)＝ｆ(Ｂ)が成立する。

（１．３）ｆ(Ａ＋Ｃ)＝ｆ(Ａ＋Ｃ＋Ａ＋Ｂ)=ｆ(Ｃ＋Ｂ)＝０

（１．４）中央に置けば残るのは{ｎ−１，ｎ−１}であるから。

定義３，状態の同値関係

（１．１）（１．３）よりｆ(Ａ＋Ｂ)＝０は同値関係を定めます。

よってｆ(Ａ＋Ｂ)＝０ならば，ＡとＢは判定関数ｆのもとで同値であると言い，
Ａ≡Ｂ(ｆ)，または単にＡ≡Ｂで表します。

定義４，整数の同値関係

　Ａ＝{ｎa},Ｂ＝{ｎb}とすると
ｆ({ｎa，ｎb})＝０ならば，{ｎa}≡{ｎb}である。

このとき整数ｎaとｎbは判定関数ｆのもとで同値であると言い，
ｎa≡ｎb(ｆ)，または単にｎa≡ｎbで表します。

定義５，同値類の値

定義４の同値関係により，０以上の整数を同値類に分類することができます。
（ここでは−１は除外して置きます）

そして，同値類をそれに含まれる最小の要素の値で表します。
ｎが含まれる同値類の値（則ち最小の要素の値）をｇ(ｎ)で表します。
当然の事ながらｎ≡ｇ(ｎ)が成立します。

また，
Ａ＝{ｎ1，ｎ2，．．．ｎr}，
Ｂ＝{ｇ(ｎ1)，ｇ(ｎ2)，．．．ｇ(ｎr)}
のとき，Ｂ＝ｇ(Ａ)と表します。

命題２，判定関数の性質２

（２．１）　Ａ≡Ｂならばｆ(Ａ)＝ｆ(Ｂ)
（２．２）　ｆ(Ａ)＝ｆ(ｇ(Ａ))

証明

（２．１）　ｆ(Ａ)＝ｆ(Ａ＋Ａ＋Ｂ)=ｆ(Ｂ)

（２．２）　
　ｆ(Ａ＋ｇ(Ａ))
＝ｆ({ｎ1，ｇ(ｎ1)，ｎ2，ｇ(ｎ2)，．．．ｇ(ｎr)}
＝ｆ({ｎ2，ｇ(ｎ2)，．．．ｇ(ｎr)}
＝０

よりＡ≡ｇ(Ａ)が成り立つ。
よってｆ(Ａ)＝ｆ(ｇ(Ａ))。

以上でやや面倒な準備が終わりました。

２．判定関数ｆの求め方（シラミ潰し）

　これまでの議論より判定関数ｆに対する幾つかの性質が明らかにされましたが，これだけでｆの実際の値が求められるわけではありません。
しかし，これらの性質を用いることで判定を大幅に簡単化することができます。

ｆの実際の値を求める基本となるのは次の事実です。

　もし，先手がある場所に碁石を置いたとき，残ったパターンＡ’が後手必勝となるような手が存在するとき，もとのパターンＡは先手必勝である。
そのような手が存在しないときは後手必勝である。

これは，漸化式

ｆ(Ａ)＝１−Π
すべてのＡ’ 		ｆ(Ａ’)で表すことができます。

　Ａのｉ番目の連続領域のｊの位置に碁石を置いた時のＡ’は
Ａの要素ｎiを２つの要素(ｎi-ｊ-１)と(ｊ−２)で置き換えることにより得られます。

　したがって，漸化式は次のように表すことができます。

ｆ(Ａ)＝１−Π
1≦i≦r,1≦j≦[(ni+1)/2] 		ｆ(Ａ＋{ｎi，ｎi-ｊ-１，ｊ−２})

ただし，［　］はガウスの記号（整数部分）です。

　これと命題１を用い，初期値として
ｆ({ })＝ｆ({０})＝ｆ({−１})＝０，
を使えば，機械的にｆ(Ａ)を求めることができます。

　さらに命題２を用いて

ｆ(Ａ)＝１−Π
1≦i≦r,1≦j≦[(ni+1)/2] 		ｆ(ｇ(Ａ＋{ｎi})＋ｇ({ｎi-ｊ-１，ｊ−２}))

とすれば計算を大幅に減らすことができます。

　このためには，Ａの最大の要素以下整数についてｇ(ｎ)を知って置く必要がありますが，
これにはｆ(ｎ，ｍ)が必要です。
そのまま適用すると無限再帰に陥りますので，
ｇ(ｎ)を求める時だけは一時的にｇ(ｎ)＝ｎとして漸化式を用います。

３．結果（シラミ潰し）

　２．の方法により204以下の整数に対して調べたところ，９つの同値類に分類されることが判りました。
その結果を以下に示します。
最初の同値類０の要素がゲームが後手必勝となる碁盤の長さです。

{0, 4, 8, 14, 20, 24, 28, 34, 38, 42, 54, 58, 62, 72, 76, 88, 92, 96, 106, 110, 122, 126, 130, 140, 144, 156, 160, 164, 174, 178, 190, 194, 198},

{1, 2, 6, 7, 21, 22, 26, 27, 35, 36, 40, 41, 55, 56, 60, 61, 69, 70, 74, 75,89, 90, 94, 95, 103, 104, 108, 109, 123, 124, 128, 129, 137, 138, 142, 143, 157, 158, 162, 163, 171, 172, 176, 177, 191, 192, 196, 197},

{3, 11, 12, 16, 17, 25, 31, 37, 45, 46, 51, 59, 71, 79, 80, 93, 105, 113, 114,127, 139, 147, 148, 161, 173, 181, 182, 195},

{5, 9, 10, 18, 19, 23, 39, 43, 44, 52, 53, 57, 65, 73, 77, 78, 86, 87, 91, 99,107, 111, 112, 120, 121, 125, 133, 141, 145, 146, 154, 155, 159, 167, 175, 179, 180, 188, 189, 193, 201},

{13, 29, 33, 47, 48, 63, 67, 81, 82, 97, 101, 115, 116, 131, 135, 149, 150, 165, 169, 183, 184, 199, 203},

{15, 30, 49, 50, 64, 83, 84, 98, 117, 118, 132, 151, 152, 166, 185, 186, 200},

{32, 66, 100, 134, 168, 202},

{68, 102, 136, 170, 204}, 

{85, 119, 153, 187}
　これをみるとｇ(ｎ)はほぼ周期３４の周期関数となっていることが判ります。
ほぼと言ったのは次の５カ所で
ｇ(ｎ)！＝ｇ(ｎ−３４)となっているからです。
　ｇ(４８)＝１３！＝　ｇ(１４)＝０
　ｇ(５０)＝１５！＝　ｇ(１６)＝３
　ｇ(６５)＝　５！＝　ｇ(３１)＝３
　ｇ(６８)＝６８！＝　ｇ(３４)＝０
　ｇ(８５)＝８５！＝　ｇ(５１)＝３
　それ以降は周期的に見えますが，ずっと続くかどうかは良く判りません。
なんだか，ちょっと気持ちわるいですね。
プログラムのミスではないと思っているのですが？？。

４．同値類を用いた判定法

　同値類が上記９つのみであると仮定すると
（または１０番目の同値類があらわれるｎより小さな数のみで構成されるパターンに対して），
パターンが先手必勝か後手必勝かは次のように判定できます。

　命題２からパターンの中の整数ｎをｇ(ｎ)で置き換えてもｆの値は変わりません。
また，命題１よりこうして得られたパターンから０および同じ値の２つの要素を除去して考えることができます。
このことを用いてパターンを簡単化すると，その結果は
{1, 3, 5, 13, 15, 32, 68, 85}の部分集合として表されます。

　したがって，有限個（２8）のパターンについて
ｆ(Ａ)が求められればよいことになります。
そして，力ずくで調べなくても以下のように判定できます。
（Ａは既に上記の方法で簡略化されているものとします。）

Ａの要素の数が０の場合は，ｆ({ })＝０ です。

Ａの要素の数が１つの場合は，ｆ(Ａ)＝１ です。
　（同値類０のみが後手必勝）

Ａの要素の数が２つの場合も，ｆ(Ａ)＝１ です。
　（同値関係の定義より）

Ａの要素の数が３つの場合で，ｆ(Ａ)＝０となるのは

{1,3,5},{1,13,15},{1,68,85},{3,15,32},{5,13,32}
の５通りだけです。
（これはシラミつぶしで調べました）。

　Ａの要素の数が４以上の場合は，必ず

{1,3,5},{1,13,15},{1,68,85},{3,15,32},{5,13,32}
のいずれかのパターンの２つの要素を含みます。

したがって

ｆ({ｎ1，ｎ2，ｎ3})＝０ならば，
　ｆ({ｎ1，ｎ2}＋Ｂ)＝ｆ({ｎ3}＋Ｂ)

により要素の数が１つ少ない場合に変換できます。

これらを用いれば，要素の数がいくつであってもｆ(Ａ)を求めることができます。

　この簡単化を逆に用いることにより要素数３つの後手必勝パターンから要素数４以上の後手必勝パターンを順次生成することができます。
その結果は以下のようになりました。

要素数４つの後手必勝パターンは

{1, 3, 13, 32},
{1, 5, 15, 32},
{3, 5, 13, 15},
{3, 5, 68, 85},
{13, 15, 68, 85}
の５通りだけです。

要素数５つの後手必勝パターンは

{3, 13, 32, 68, 85},
{5, 15, 32, 68, 85}
の２通りだけです。

要素数６つの後手必勝パターンは

{1, 3, 15, 32, 68, 85},
{1, 5, 13, 32, 68, 85}
の２通りだけです。

要素数７つの後手必勝パターンは

{1, 3, 5, 13, 15, 68, 85}
の１通りだけです。

要素数が８つ（則ち全部）の場合は先手必勝です。

したがって，空集合を除くと１５パターンのみが後手必勝です。

　したがって，まず，Ａに対してｇ(Ａ)を求め，
ｇ(Ａ)のなかの０と同じ値の数の組を除いた結果が空集合か上記１５パターンであれば後手必勝，
さもなければ先手必勝です。

　以上よりｇ(ｎ)と１５パターンを憶えておけば，計算や試行錯誤なしに任意のパターンが先手必勝か後手必勝かを判定できることが判りました。
　なお，ｇ(ｎ)には前述のようにほぼ周期的ですので，すべてを覚えておく必要はありません。

◆石川県　MJ さんからの解答

【問題１】

後手有利

先手１→後手３→終了
先手２→後手４→終了

【問題２】

先手有利

始めに先手が３を取ればよい
先手３→後手１→先手５→終了
先手３→後手５→先手１→終了

【問題３】

先手有利

始めに先手が１を取ればよい（６でもよい）
先手１→後手３→先手５→終了
先手１→後手４→先手６→終了
先手１→後手５→先手３→終了
先手１→後手６→先手３→終了

【問題４】

先手有利

始めに先手が２を取ればよい
先手２→後手４→先手６→終了
先手２→後手５→先手７→終了
先手２→後手６→先手４→終了
先手２→後手７→先手４→終了

【問題５】

後手有利

１→３→５ｏｒ６→８→終了
　　　→７ｏｒ８→５→終了

２→６→４→８→終了
　　　→８→４→終了

３→７→１→５→終了
　　　→５→１→終了

４→６→１ｏｒ２→８→終了
　　　→８→１→終了
【問題６】

先手有利

始めに先手が５を取ればよい

５→１→７→３→９→終了
　　　　　→９→３→終了

５→２→８→終了

５→３→７→１→９→終了
　　　　　→９→１→終了
【問題７】

先手有利

始めに先手が１を取ればよい

１→３→５→７→９→終了
　　　　　→９→７→終了
　　　　　→８→１０→終了
　　　　　→１０→８→終了

１→４→８→６→１０→終了
　　　　　→１０→６→終了

１→５→９→３→７→終了
　　　　　→７→３→終了

１→６→８→３ｏｒ４→１０→終了
　　　　　→１０→３→終了

１→７→３→５→９→終了
　　　　　→９ｏｒ１０→５→終了

１→８→４→６→１０→終了
　　　　　→１０→６→終了　　　　　　　　　　　　　　　　

１→９→５→３→７→終了
　　　　　→７→３→終了

１→１０→５→３→７→終了
　　　　　　→７ｏｒ８→３→終了

◆愛知県　Y.M.Ojisan さんからの解答

【問題１〜８】

N 1:先手必勝
0:後手必勝		 必勝法初手
3 1 中央
4 0 　
5 1 中央
6 1 端から２番目
7 1 中央
8 0 　
9 1 中央
10 1 端から２番目
11 1 中央
12 1 端から４番目
13 1 中央
14 0 　
15 1 中央
16 1 端から２番目
17 1 中央
18 1 端から５番目
19 1 中央
20 0 　

【おまけ１】

奇数の場合は中央をとり，真似碁をすると先手必勝。

【おまけ２】

解答ではありません。

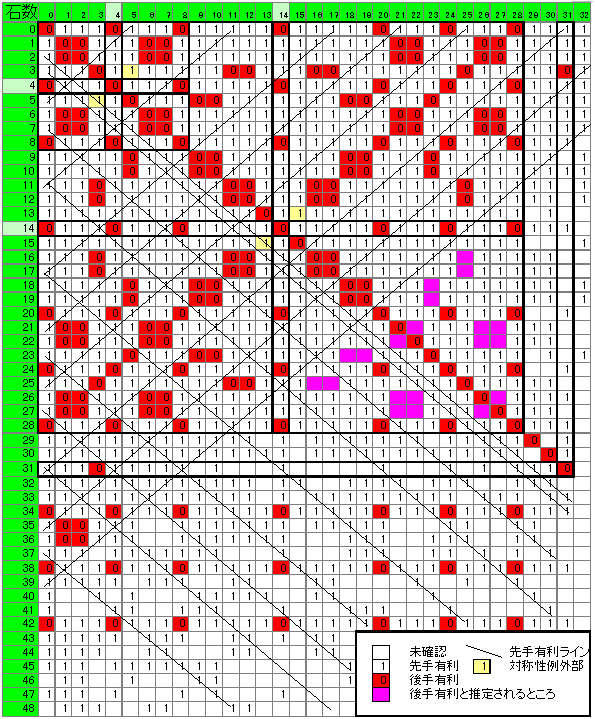
２手目ないし山が１〜２個から始めた場合の勝ち負けを下図に示します。
凡例は図中にあります。
緑のセルが初期のそれぞれの山の石の数です。
なおこれは　単に計算機によりしらみつぶしした結果です。

（４，４）および（１４，１４）を中心にした対称性がみられます。
なぜそうなるか分かりませんが，これを手がかりに簡単な必勝法がみつけられるかも。

１４〜２８領域のマゼンタの部分は現状のアルゴリズム＋ＰＣでは時間がかかりすぎて確認できない領域ですが，これがまた対称性から予測される後手必勝部と一致しており，後手有利と予測されます。

なお，（３１，３１）が更なる対称性の中心である兆候があります。

勝敗判定のプログラムに，簡単な経験則を入れ込んだら，
Ｎ＝６４まで簡単に判定がつく(500MHz)ようになり，
Ｎ＝４，１４，３１中心の対称性の予測も確認できました。

判定ソフトは腕力計算アルゴなので，核の部分は非常にシンプルです。
バグなしの確認の意味もあって，それに表示等を追加して，対戦ソフトにしました。
６４bit整数はＡＮＳＩ規格では無いので，｛３２以下　２山｝の初期値ではじめるものを，送付いたします。
なお，C++ による　Ｃonsole　／　 DOS window用です。

　◆　問題へもどる

　◆　今週の問題へ

数学の部屋へもどる