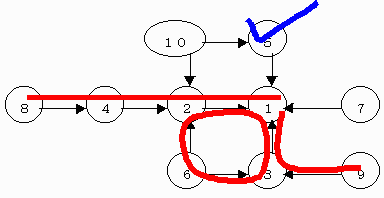
◆宮城県 アンパンマン さんからの解答
【問題1−1】 5のカード
【問題1−2】 8のカード
【問題1−3】
先手、最初は4あるいは6を選びます。
4の場合3,6,9組と 5,10組があります。
後手がこの二組の中から選ぶ場合、先手が残りの組から選ぶ。
そうじゃない場合(つまり7か8の場合)、先手が残りのカード(7か8)を選ぶ。
6の場合4,8組と 5,10組があります。
後手がこの二組の中から選ぶ場合、先手が残りの組から選ぶ。
そうじゃない場合(つまり7か9の場合)、先手が残りのカード(7か9)を選ぶ。
【問題2】
a,dは偶数、b,cは奇数とします。
(c-b,a-d)=p (c-bとa-dの最大公約数)、
(c+b,a+d)=qとします。
| c2-b2=a2-d2より (c-b,a+d)= | c-b p |
| (c2-b2,a+d)=a+d より | c-b a+d | = | p ― q |
| (a-d)2+(c-b)2 (a+d)2+(c+b)2 |
| ={ | (c-b)(c+b) a+d | } | 2+ | (c-b)2 (a+d)2+(c+b)2 |
| = | (c-b)2 (a+d)2 |
| = | p2 q2 |
両辺に1を足すと
| 2(a2+b2+c2+d2) (a+d)2+(c+b)2 | = | p2+q2 q2 |
a2+b2+c2+d2=2n より
| n= | p2+q2 4 | ・ | (a+d)2+(c+b)2 q2 |
p,qは偶数なので
| p2+q2 4 | は整数>2(nは奇数)。 |
qはc+bとa+dの最大公約数なので
| (a+d)2+(c+b)2 q2 | は整数です(>2)。 |
上記よりnは2つの約数の積で表せます。
◆熊本県 ELF さんからの解答
【問題1−1】 5
【問題1−2】 8
【問題1−3】
先手が有利。
勝利条件は自分の手の後に偶数枚のカードを残すこと。
・先手が6を選んだ場合。
1,2,3が選べないので、残りは6枚。
このうち、4と8,5と10は互いに約数と倍数の関係にあることに注意する。
後手が4を選んだら5を選び、7を選んだら9を選び、8を選んだら10を選ぶ(ペアの逆は省略)ことで勝利が確定する。
・先手が4を選んだ場合。
1,2が選べないので、残りは7枚。
ただし、3と6,3と9,5と10は互いに約数と倍数の関係にあり、3が重複しているのがポイントとなる。
後手が3を選んだら10を選び、5を選んだら6または9を選び、7を選んだら8を選ぶ(ペアの逆は省略)ことで勝利が確定する。
先手が1,2,3のいずれかを選ぶと、後手が6を選ぶことにより必敗。
先手が5を選ぶと、後手が10を選ぶことにより必敗。
先手が7を選ぶと、後手が4を選ぶことにより必敗。
先手が8,10を選ぶと、後手が7を選ぶことにより必敗。
先手が9を選ぶと、後手が2を選ぶことにより必敗。
よって、必勝パターンは先手が4か6を選んだ場合に限る。
◆福岡県 古豚 さんからの解答
【問題1−1】 5
【問題1−2】 8
【問題1−3】
先手必勝。
先手は最初に 4または6を取る。
後は、後手の取り方によって最善手をつくせば先手が勝つ。
全てを並べて考えました。
規則性は見つけることができませんでした。
【問題2】
a,b,c,dのうち、
aとcは偶数、bとdは奇数、
a−c、d−bは正の数とする。
a+c,b+dの最大公約数をG、
a−c,d−bの最大公約数をgとする。
| n= | G2+g2 4 | × | (a+c)2+(d+b)2 G2 |
で表されます。
偶数、奇数の条件から、
| n= | G2+g2 4 | は整数であることは明らか。 |
また、(a+c)(a-c)=(d+b)(d-b)から、
(a+c)=pG、(d+b)=qG
(a-c)=qg、(d-b)=pgとおいて、
| G2+g2 4 | × | (a+c)2+(d+b)2 G2 | =n |
は証明できます。
◆愛知県 Y.M.Ojisan さんからの解答
【問題1−1】 5

【問題1−2】 8
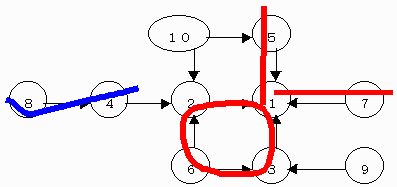
【問題1−3】
先手有利
初手「6」必勝
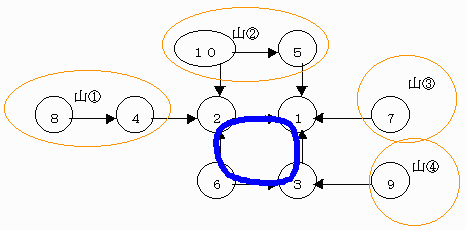
あとは 三山崩しの方法。
(1個+2個+2個+1個)
なお、初手「4」も先手必勝手だが、
3−6−9の山が三山崩しで2個の山と等価である説明がちょっとだけ煩雑なので省略。
【問題2】
n=a2+b2=c2+d2 ―――(1)
を満足する ((a,b),(c,d))の組み合わせを 偶奇性で分類すると、下記3タイプである。
(ア)((偶数,偶数),(偶数,偶数))
(イ)((偶数,奇数),(偶数,奇数))
注((偶数,奇数),(奇数,偶数))はc d交換で(イ)に集約
(ウ)((奇数,奇数),(奇数,奇数))
注((偶数,偶数),(奇数,奇数))は (1)を満足しない。
(ア)の場合は n=2×(2×整数) であり2つの約数の積に分解できる。
(イ)と(ウ)の場合を以下に述べる。
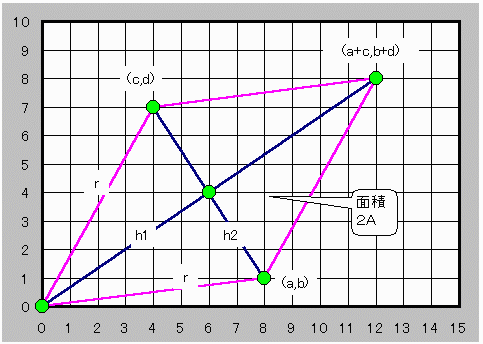
図に示すように、
(0,0) (a,b) (a+c,b+d)(c,d)を頂点とする4角形を考えるとき(1)により
一辺が![]() のひし形である。
のひし形である。
対角線長の半分をそれぞれh1 、 h2とする。
このとき、a,b,c,d>0としてよいので、
h1>h2 である。 ―――(2)
ひし形の面積を2Aとおくとき、h1と h2が直交するので下式が成立する。
A=h1× h2=|ad−bc|/2 ―――(3)
重心は (a+c,b+d)/2 であって,(イ)(ウ)何れの場合も下記により格子点上である。
(a+c,b+d)/2=(偶数,偶数)/2 =(整数、整数) ―――(4)
また(3)より
|ad-bc|
=|偶数−偶数|=偶数 (イ)の場合
=|奇数−奇数|=偶数 (ウ)の場合
であるので A=偶数/2は整数である。―――(5)
また、ひし形(h1と h2が直交)なので
n=r2=h12+h22 ―――(6)
さらに 重心が格子点上であるから
h12={((a+c)/2)2+((b+d)/2)2}}=整数1
h22={((a-c)/2)2+((b-d)/2)2}}=整数2
整数1>整数2であり、(3)A=(h1×h2)より
A2=h12 ×h22=整数1×整数2 ―――(7)
<蛇足注>
Aが素数であるためには整数2は1でなければならないが、そのためには
a=c b=d+1等でなければならず(1)を成立させ得ない。
よってAは合成数である。
●h12:整数1とh22:整数2に共約数αがあるとき nは下記のように約数の積に分解できる。
n= h12+h22=α×(h12/α+h22/α) ―――(8)
<蛇足注>
h12/α と h22/α は(7)よりそれぞれ平方数である。
●一方 h12:整数1とh22:整数2に共約数がないと仮定すると(7)より
h1、h2は整数で 互いに素 でなければならない。―――(9)
重心座標を(gx,gy)とするとき、
△(0,0)-(gx,0)-(gx,gy) と △(gx,gy)-(gx,b)-(a,b) は
相似比 h1:h2で相似である。
即ち下式でなければならない。
gx = h1/h2 ×(gy-b)
gy = h1/h2 ×(a-gx)
ところが(4)よりgx,gyは整数でなければならず、
h1とh2は互いに素なので、
(gy-b) (a-gx)はh2の倍数である必要がある。
一方 0<(gy-b)と(a-gx)<h2 であり h2の倍数にできない。
すなわち、整数1と整数2に共約数がないとの仮定は正しくなく、共約数αが必ず存在する。
>>> 以上からnは必ず約数の積に分解できるといえる。
なお、その約数の一部はh12とh22の共約数である。
◆ 問題へもどる
◆ 今週の問題へ