◆静岡県 ヨッシーさんからの解答。
【問題1】
1×1の正方形が 5×4=20
2×2の正方形が 4×3=12
3×3の正方形が 3×2= 6
4×4の正方形が 2×1= 2 の合計40個
【問題2】
左側の5×2のマスを含む正方形は1×1の正方形8個のみ。
よって、それ以外の5×4の部分で出来る正方形40個(【問題1】より)と合わせて、
8+40=48(個)。
【問題3】・1×1
a×b=ab
・2×2
(a−1)(b−1)=ab−(a+b)+12
・3×3
(a−2)(b−2)=ab−2(a+b)+22
・・・・・・
・b×b
(a−b+1)(b−b+1)=ab−(b−1)(a+b)+(b−1)2
正方形の個数は
b×ab−{1+2+・・(b−1)}(a+b)+{12+22+・・(b−1)2}
| =ab2− | b(b−1)(a+b) 2 | + | b(b−1)(2b−1) 6 |
| = | b(b+1)(3a−b+1) 6 | (個) |
ちなみに、a=bだと、2乗和の公式
| a(a+1)(2a+1) 6 |
になります。よく考えれば、当たり前ですが。
◆大分県の小学生 べっち さんからの解答。
【問題1】
1目盛四方が20個
2目盛四方が12個
3目盛四方が6個
4目盛四方が2個
20+12+6+2=40
答 40個
【問題2】
48個(数えました)
◆北海道の中学校2年生 ぴよこ さんからの解答。
【問題1】
40個(問題2の解答を使いました。)
【問題2】
1×1が28個
2×2が12個
3×3が6個
4×4が2個
の合計48個
◆東京都 鳳 奥人 さんからの解答。
【問題1】
| サイズ(1辺) | 1 | 2 | 3 | 4 | 計 |
| 個 数 | 20 | 12 | 6 | 2 | 40 |
【問題2】
まず、赤い部分も含めた全体では・・・
| サイズ(1辺) | 1 | 2 | 3 | 4 | 5 | 計 |
| 個 数 | 30 | 20 | 12 | 6 | 2 | 70 |
うち、赤い部分を「含む」ものは、
| サイズ(1辺) | 1 | 2 | 3 | 4 | 5 | 計 |
| 個 数 | 2 | 8 | 6 | 4 | 2 | 22 |
よって、赤い部分を含まない正方形は 70−22=48(個)。
【問題3】
1辺のサイズは1〜bですね。サイズ(1辺) 個数
1 a×b
2 (a−1)×(b−1)
3 (a−2)×(b−2)
: :
: :
n {a−(n−1)}×{b−(n−1)}
: :
: :
b−1 (a−b+2)× 2
b (a−b+1)× 1
・・・なのですが、この和を求めるということなのですよね。
| だから | b Σ n=1 | {a-(n-1)}{b-(n-1)} なのですが、 |
◆山梨県 Footmark さんからの解答。
【問題3】
a×bの長方形の格子点の数は(a+1)×(b+1)です。
そこで、各格子点が正方形の右上の頂点となる場合を考えます。
明らかに、1番左側と1番下側のL字型に並んだ各格子点には正方形は存在しません。
そこでL字型を1つ右上にずらすと、L字型に並んだ各格子点には辺長1の正方形が1つ存在します。
さらにL字型を1つ右上にずらすと、L字型に並んだ各格子点には辺長1と辺長2の正方形の2つが存在します。
さらにL字型を1つ右上にずらすと、L字型に並んだ各格子点には辺長1と辺長2と辺長3の正方形の3つが存在します。
このように、L字型に並んだ格子点を1つ右上にずらすたびに存在する正方形の数は1つずつ増えていきます。
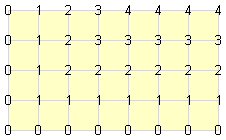
仮に、7×4の長方形を例にすると、各格子点が右上の頂点となる正方形の数は以下になります。

そこで、この各格子点における正方形の存在数を、以下のように2つの部分に分割します。
01234444 01234 444
01233333 01233 333
01222222 = 01222 + 222
01111111 01111 111
00000000 00000 000
分割された左側をL、右側をRとします。
すると、Lは以下のようにさらに展開できます。
01234 01111 00111 00011 00001
01233 01111 00111 00011 00000
L= 01222 = 01111 + 00111 + 00000 + 00000
01111 01111 00000 00000 00000
00000 00000 00000 00000 00000これは、与えられたa,bで表すと、明らかに12+22+・・b2 です。
| ∴ L= | b(b+1)(2b+1) 6 |
また、Rも与えられたa,bで表すと、
明らかに1+2+・・bの(a−b)倍です。
| ∴ R= | (a−b)b(b+1) 2 |
よって、
求める正方形の数
| =L+R |
| = | b(b+1)(2b+1) 6 | + | (a−b)b(b+1) 2 |
| = | b(b+1)(3a−b+1) 6 |
| 【答え】 | b(b+1)(3a−b+1) 6 | 個 |
◆北海道の小学生 abe さんからの解答。
【問題2】
48個
1*1 28
2*2 12
3*3 6
4*4 2
◆神奈川県の小学生 達也 さんからの解答。
sは面積です。
【問題1】
s=1→20
s=4→12
s=9→6
s=16→2
20+12+6+2=40
40個
【問題2】
s=1→28
s=4→12
s=9→6
s=16→2
28+12+6+2=48
48個
【問題3】
s=1*1→a*b
s=2*2→(a-1)*(b-1)
s=3*3→(a-2)*(b-2)
… …
s=(b-1)*(b-1)→ (a-(b-2))*(b-(b-2))
s=b*b→(a-(b-1))*(b-(b-1))
a*b+(a-1)*(b-1)+(a-2)+(b-2)+…+(a-(b-1))*(b-(b-1))=c
c個
◆滋賀県の中学校2年生 kazuya さんからの解答。
【問題1】
面積1の正方形 4×5=20(個)
面積4の正方形 3×4=12(個)
面積9の正方形 2×3= 6(個)
面積16の正方形 1×2= 2(個)
計 40個
【問題2】
面積1の正方形 28個
面積4の正方形 12個
面積9の正方形 6個
面積16の正方形 2個
計 48個