◆滋賀県 ippei さんからの解答。
【問題1】
線分ABの垂直2等分線と線分BCを1:3に内分する点からBCに立てた垂線が交わる点が求めるP
◆山梨県 Footmark さんからの解答。
【問題1】
【答え】
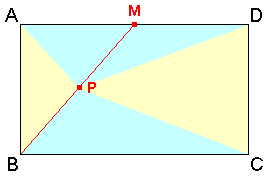
ADの中点をMとする。
求める点PはBMの中点。
[ 証明 ]

明らかに、△PAB:△PCD=1:3。
△PABの面積をSとすると、
△PAB+△PCD=△PBC+△PDA=4S。
すると、△PBC=△PDA故、△PBC=2S。
よって、△PAB:△PBC=1:2。
以上より、△PAB:△PBC:△PCD=1:2:3。
証明終わり。
◆千葉県 なのはな子 さんからの解答。
【問題2】
4つの三角形の面積比が1:2:3:4
1+2+3+4=10
正方形を10で割り切れる数の正方形に分割すればできる。
◆山梨県 Footmark さんからの解答。
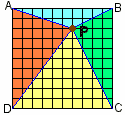
【問題2】
反時計回りか時計回りに、面積比を1:2:3:4にするのは、
1+3≠2+4 と、2組の向かい合った三角形の面積和が異なるため不可。
反時計回りか時計回りに、面積比を1:2:4:3にするのは、
1+4=2+3 と、2組の向かい合った三角形の面積和が等しいため可能。
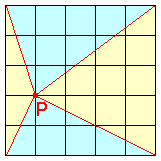
【問題3】
● 正六角形
反時計回りか時計回りに、面積比を1:2:3:6:5:4とすると、
1+6=2+5=3+4=7 と、3組の向かい合った三角形の面積和が等しいため、一見【問題2】同様可能に思える。
ところが、向かい合った三角形の面積比は3組とも互いに素である。
それ故、どうしても正六角形の各対辺間を7(=1+6=2+5=3+4)等分しなければならない。

すると、各組6本ある3組の7等分線において、どの交点も左図のように3直線の交点とはならない。
逆に、3直線の交点にすると、今度は右図のように正六角形とはならない。
よって、条件を満たす点Pは存在しない。
[ 補足 ]
正2n角形(nは3以上の整数)においては、
それ故、この2条件を満たしても、必ずしも点Pが存在するとは限らない。
(一例) 反時計回りか時計回りに、面積比が1:2:3:5:4:3は不可。
● 正五角形
正奇数角形となると、「向かい合った三角形の面積和がいずれも等しい。」は利用できない。
そこで、以下のようにする。
まず、任意の正五角形の中心から各頂点を通る5本の半直線を引く。
(図の青線)
次に、中心からの距離が1:2:3:4:5(順序は問題としない)である5つの点を異なる半直線上にとる。
(図の青点)
さらに、その点を通り半直線に垂直な5本の直線を引く。
(図の黒線)

すると、5角とも等しい五角形が必ず形成される。
元の正五角形の中心を点Pとすると、明らかに点Pが存在するなら形成された五角形は正五角形の筈である。
ところが、5点を5つの半直線上にどのように割り振っても正五角形は形成されない。
(五角形が1番歪にならないのは、明らかに1,3,5,4,2の並びのときなので、このときの吟味だけでも十分。)
よって、条件を満たす点Pは存在しない。