◆広島県 清川 育男 さんからの解答。
【問題１】
Bは平方数であるから、
B≡0または1(mod 3)
90A≡0 (mod 3)であるから、
50B≡O (mod 3)
2B≡0 (mod 3)
B≡0 (mod 3)
B=N2
３桁の数であるから、
10≦N≦31 で３の倍数でなければならない。
N=12,15,18,21,24,27,30
N=15 のとき B=225
50B=11250
A=125
Aは２桁の数であるから、題意を満たす候補は、
N=12，B=144，A=80
90*80=50*144=7200
これは題意を満たす。
答え A=80，B=144
◆京都府 ぺぺぺ さんからの解答。
【問題１】
９０Ａ＝５０Ｂ
| Ａ＝ | ５ ９ | Ｂ −−−(1) |
条件から１０≦Ａ＜１００
式(1)を代入すると
| １０≦ | ５ ９ | Ｂ＜１００ |
１８≦Ｂ＜１８０
Ｂは３桁の平方数なので候補は
１００、１２１、１４４、１６９のいずれか
Ａは自然数なので式(1)から、Ｂは９で割り切れる
上記のうち９で割り切れるのは１４４のみ
Ｂ＝１４４
式(1)からＡ＝８０
答え Ａ＝８０，Ｂ＝１４４
【問題２】
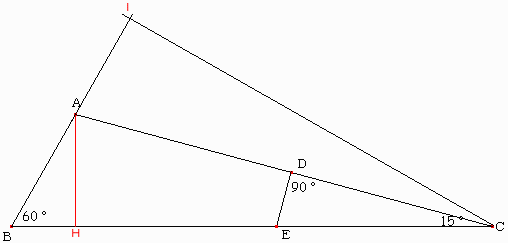
∠ＣＥＤ＝75度
ＡからＢＣに下ろした推薦の足をＨとすると
∠ＨＡＣ＝75度
二角相等で△ＡＣＨ∽△ＥＣＤ
これら2つの三角形の斜辺の比は２：１なので
面積比は４：１となる
つまり△ＡＣＨ＝△ＥＣＤ×４
次にＣからＡＢの延長線に下ろした垂線の足を Ｉ とすると
△ＡＣＩと△ＡＣＨについて
∠ＩＣＡ＝15度
∠ＣＡＩ＝75度
辺ＡＣ共有
よって△ＡＣＩ≡△ＡＣＨ
以上から
求める面積△ＡＢＣ＋△ＣＤＥ×４
＝△ＡＢＣ＋△ＡＣＩ
＝△ＢＣＩ
| ＢＩ＝ | ２ ２ | ＝ |
ＣＩ＝× ＝ |
| △ＢＣＩ＝ | × ２ | ＝ |
答え
◆滋賀県の中学校１年生 西尾 恭史 さんからの解答。
【問題１】
Aは２桁の自然数なので最高は９５。
Ａ：Ｂ＝５：９
９５×１．８（９÷５）＝１７１。
１００以上１７１未満で平方数は
１００・１２１・１４４・１６９ の４つ。
この中で９の倍数なのは、１４４。
１４４×（５÷９）＝８０
Ａ＝８０，Ｂ＝１４４
◆東京都 鳳 奥人 さんからの解答。
【問題１】
90A＝50B だから B=(9/5)A
Ｂが平方数になるためには、Ａは平方数に５をかけた数でなければいけない。
（Ｂは自然数だからＡは５で割りきれなければならないし、９がすでに平方数だからＡを５で割った商も平方数でないとＢが平方数にならない）
Ａは２桁だから、Ａの候補は20, 45, 80の３つ。
このうち、Ｂが３桁になるのはＡ＝８０のときだけ。
このときＢ＝１４４。
答え：Ａは８０、Ｂは１４４。
◆神奈川県 ココちゃん さんからの解答。
【問題１】
およその合計金額をCとして大体いくらかと考えました。
Ａは２桁であるからおよその合計金額Cは
９０円×９９個＝８９１０円より少ないはず
３桁の平方数Ｂは１７８より小さい
(およその合計金額Cを50円で割ると8910/50=178あまり10）
そのとき３桁の平方根は１０（平方数は１００）から１３（平方数は１６９）
B=１００本のとき合計金額=５０００、９０円で割れない
B=１２１本のとき合計金額=６０５０、９０円で割れない
B=１４４本のとき合計金額=７２００、９０円で割ると８０個
B=１６９本のとき合計金額=８４５０、９０円で割れない
よってAは８０、Bは１４４
◆兵庫県 たまはち さんからの解答。
【問題１】
問題文より90A＝50B →9A＝5B。−(1)
よってAは因数として5（5はAの約数）、Bは因数として9（9はBの約数）であることが分かる。−(2)
また、Bは3桁の平方数であるから、
B=100、121、144、169、196のいずれかである。
これらを素因数分解すると、
B＝100＝10×10＝（2×5）×（2×5）
B＝121＝11×11
B＝144＝12×12＝（2×2×3）×（2×2×3）＝（2×2×2×2）×（3×3）
B＝169＝13×13
B＝196＝14×14＝（2×7）×（2×7）となる。
(2)の条件より、Bは9を因数として持つわけだから、B＝144であることが分かる。
よって、(1)式よりA＝80が分かる。
そして、これは(2)の条件を満たしている。
答え A＝80、 B＝144
【問題２】
まず、辺ABを点A側へ延長した線に、点Cから垂線を下ろす。
この交点をFとする。
このとき、∠CFB＝90°、∠FBC＝60°であることから、∠FCB＝30°となる。
よって∠FCA＝15°。
これから、∠FAC＝75°となる。
また、∠DEC＝75°であることから、△ECDと△AFCは、3つの角が等しいので、相似な図形であることが分かる。
また、問題条件より、辺AC：辺CE＝2：1であることから、
△AFC：△ECD＝2：1となる。
よって△AFCの面積S1と△ECDの面積S2は
S1＝4×S2となる。
問題より、求めるべき面積は、△EDCの4倍+△ABCであるから、
△EDC（S2）×4+△ABC ＝ △AFC（S1）+△ABC ＝ △FBC
と同じことである。
よって、求める面積は、直角三角形FBCの面積ということになる。
辺BC＝2であり、また△FBCの角度は、それぞれ30°60°90°であることから、
辺FC＝、辺CF＝
（∵1：2：の比率）
となり、△FBCの面積はとなる。
よって、求める面積は である。
答え