（N-1）人 / １ヶ国
［左表の説明］
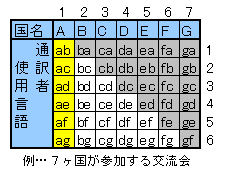
例えば、７ヶ国が交流会に参加する場合。
各参加国は他国の事情がわからないため、とりあえず(Ｎ−自国)ヶ国語の通訳者(Ｎ−１)人を同伴する。
すると、(Ｎ−１)ＸＮ人の通訳者が集まる。
同じ２ヶ国語を使う通訳者が２人ずつになるので、全通訳者のうち半数は不要となる。
◆東京都 六年目起き太郎 さんからの解答。
代表国を１つ決めてその国以外の人たちがその国の言葉を話せる通訳者を連れてくればいいと思います。
よって、合計N-1人。
代表国と話す時は、その国の通訳者､
それ以外の２国が話す時は､その国の通訳者をそれぞれ使い、高々２人の通訳者で会話できる。
問題の意図を勘違いしてるのでしょうか？
◆千葉県 なのはな子 さんからの解答。
1.参加国数がN(≧2)とすると、どの国同士も言葉が交わせるために必要な通訳者の人数は？
（N-1）人 / １ヶ国
［左表の説明］
例えば、７ヶ国が交流会に参加する場合。
各参加国は他国の事情がわからないため、とりあえず(Ｎ−自国)ヶ国語の通訳者(Ｎ−１)人を同伴する。
すると、(Ｎ−１)ＸＮ人の通訳者が集まる。
同じ２ヶ国語を使う通訳者が２人ずつになるので、全通訳者のうち半数は不要となる。
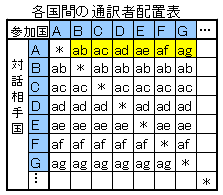2.ある国と対話するための通訳者を探し出す方法
［左表の説明］
ある国が同伴してきた通訳者を全員使う。
例えばＡ国の通訳者を選ぶとする。
(abさん、acさん、 adさん、 aeさん、 afさん、 agさん)
・Ａ国以外の国がＡ国と対話する場合
Ａ国が同伴してきた通訳者の中から、自国語を使う通訳者を選ぶ。(1人)
・Ａ国以外の国がＡ国以外の国と対話する場合
Ａ国が同伴してきた通訳者の中から、自国語を使う通訳者と、対話する相手国の言語を使う通訳者を選ぶ。
(対話する相手国の数+1)人
3.上のケースでは、多くとも何人の通訳者を経由すれば対話が可能か？
(Ｎ−１)人の通訳者を経由すれば対話が可能。
・Ａ国以外の国は、自国語の通訳者と対話相手国の言語の通訳者(２ヶ国間なら２人、３ヶ国間なら３人)を経由すれば対話が可能。
・Ａ国は、対話相手国の言語の通訳者(２ヶ国間なら１人、３ヶ国間なら２人)を経由すれば対話が可能。
『各参加国がある1つの国が同伴してきた通訳者全員を使うことで、各参加国間に1つの共通語ができる。
参加国すべての発言は、各々の通訳者によって同時に各国語に通訳される。』
◆千葉県 なのはな子 さんからの解答訂正。
「六年目起き太郎」さんの解答を見て、やはり私は『問題』の意味を読み違えていたようだと思いました。
訂正させてください。
訂正した表です。
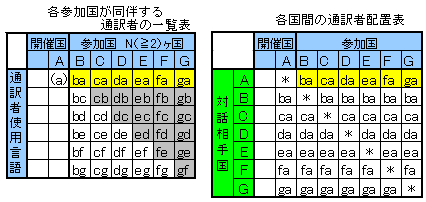
また、次の３点を訂正します。
【感想】
問題の意味の解釈が難しく、正確に把握できません。
3.の『多くとも何人の通訳者を経由すれば…』の「多くとも」の意味は、いまだによくわかりません。
正しいかどうかはわかりませんが、参加国(N≧2)には開催国は含まないと解釈しました。
◆愛知県 迷子の雄猫 さんからの解答。
１．開催国が、参加国それぞれに対して、同伴させる通訳者の通訳できる言語を指定できる場合
参加国それぞれ一人ずつの通訳を同伴させればよい。
１．の証明
１国が２国語の通訳を同伴させる
２国が３国語の通訳を同伴させる
３国が４国語の通訳を同伴させる
（中略）
Ｎ国が１国語の通訳を同伴させる
１．の場合に経由することが必要な人数
多くとも（Ｎ／２）人（端数切り捨て）人の通訳者を経由すれば対話が可能
おっと、こんな回りくどいことをしなくても良いですね（汗）
すべての参加国が、特定の言語との通訳者を同伴すればいいのです。（笑）
Ｘ国語 → 特定の言語 → Ｙ国語と、多くとも２人の通訳者を経由すれば対話が可能です。
２．開催国は、参加国のリストを提供するだけで、参加国それぞれが、同伴させる通訳者の通訳できる言語を選択する場合、
参加国それぞれ（Ｎ／２）人（端数切り捨て）ずつの通訳を同伴させればよい。
２．の証明（必要条件）
Ｎが偶数の場合Ｎ＝２kとおく。
Ｎが奇数の場合Ｎ＝２k+1とおく。
参加国が（ｋ−１）人の通訳しか同伴させなかったと仮定する。
参加国は母国語を含めてｋ種類の言語しか話せないことになる。
参加国全体を均等に２グループに分けると、それぞれのグループに少なくともｋ国が属する。
参加国全部が、それぞれのグループに属する参加国の言語しか話せない通訳者を同伴したとすると、他のグループ
に対しては通訳する方法が無い。
例：Ｎ＝８（Ｋ＝4）の場合
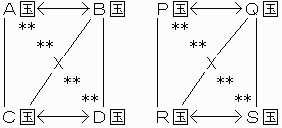
Ｎ＝９（Ｋ＝4）の場合、上の図にＴ国からＰ国、Ｑ国、Ｒ国、Ｓ国への矢印を書き加えたものを想像してください。
２．の証明（十分条件）
参加国それぞれ（Ｎ／２）人（端数切り捨て）ずつの通訳を同伴させたとする。
参加国は母国語以外にｋ種類の言語が話せることになる。
Ｘ国とＹ国が対話できないと仮定すると、以下の条件が成り立つ。
（１）Ｘ国の通訳者はＹ国語を話せない。
（２）Ｙ国の通訳者はＸ国語を話せない。
（３）Ｘ国の通訳者の話せる言語とＹ国の通訳者の話せる言語が重複していない。
よって、Ｘ国、Ｙ国、Ｘ国の通訳者の話せる国（Ｋ種類）、Ｙ国の通訳者の話せる国（Ｋ種類）
合計２Ｋ＋２の国が参加していることになる。
参加国はＮ＝２Ｋ または Ｎ＝２Ｋ＋１であるから、矛盾する。
よって、 以下の条件のうち、少なくともひとつが成り立つ。
（１）Ｘ国の通訳者がＹ国語を話せる。
（２）Ｙ国の通訳者がＸ国語を話せる。
（３）Ｘ国の通訳者の話せる言語とＹ国の通訳者の話せる言語が重複する。
２．の場合に経由することが必要な人数
多くとも２人の通訳者を経由すれば対話が可能
２．の場合 ある国と対話するための通訳者を探し出す方法
Ｘ国がＹ国に話し掛けるとする。
Ｘ国の通訳者はＹ国語を話せないのだから、（話せるなら探す必要なし（笑））
Ｘ国の代表者が「Ｙ国さん初めまして」とＸ国語で挨拶する。
Ｘ国の通訳者Ｘ１が「Ｙ国さん初めましてＸ国です」とＸ１が通訳できる言語で挨拶する。
Ｘ国の通訳者Ｘ２が「Ｙ国さん初めましてＸ国です」とＸ２が通訳できる言語で挨拶する。
（以下同様）
話し掛けられたＹ国側は、通訳者Ｙ？の通訳できる言語で挨拶された時点で、Ｙ国の通訳者Ｙ？が「Ｘ国さん初めましてＹ国です」とＹ？が通訳できる言語で挨拶する。
◆石川県 いかさま さんからの解答。
他の国と前もって連絡を取り合わないという状況下での問題と理解しました．
答えは『 [N/2]人ずつの通訳者で必要かつ十分である』です．
（［N/2］はNの半分以下で一番大きい数です．8だったら4，11だったら5）
証明（説明）は以下のとおり．
簡単のためにN=11として各国に対して，0,1,2,...,9,10と名前付けをしておきます．
すると答えは[N/2]=5人となるわけですが，まず必要であること，
つまり各国4人では，うまくすると（まずくすると）言葉を交わせない二国が存在することから示しましょう．
まず国を2グループにわけます．
A:0〜4とB:5〜10としましょう．
そして各国が（偶然にも）こうして分けられたグループ内の他の四カ国への通訳を連れてきてしまったとしましょう．
A
国0：通訳1234，
国1：通訳0234，
国2：通訳0134，
国3：通訳0234，
国4：通訳0123，
B
国5：通訳6789，
国6：通訳5789，
国7：通訳5689，
国8：通訳5679，
国9：通訳5678，
国10：通訳5678
するとグループAのどの国も，グループBのどの国とも，どんな経路を辿っても言葉を交わせません
（何人通訳を使っても同じグループ内でぐるぐる回るだけ）．
従って，少なくとも5人は必要であります．
では次に十分であること．
5人いればどんなにうまいこと（まずいこと）選んでも言葉を交わせない二国が存在しないことを示してしまいましょう．
まず，自分が0国だとして10国としゃべりたい場合を考えてみます．
10国への通訳を連れてきていればオッケー．
では連れきていない場合はどうしましょう．
10国が自分の国の通訳を連れきているか調べてみることにします．
自分の国の言葉で10国の通訳全員にしゃべりかければ，みなさん協力的なので，居れば答えてくれます．
しかし向こうもこっちの通訳を連れてきていない場合もありえます．
そうしたら今度はこっちの通訳全員で相手の通訳一人一人にしゃべりかけてみます．
もしこっちの通訳が例えば5国への通訳を連れていたとして、向こうも5国の通訳を連れきていれば彼ら彼女らを通して会話を楽しめます．
これならうまくいきそうです．
うまくいくことを証明します．
それぞれの通訳は5人いるわけですから，つまり5つの国としゃべることができます．
0国がしゃべることのできる国々をアイウエオ国としましょう．
10国がしゃべることのできる国々をあいうえお国としましょう．
もちろん同じ国相手の通訳を二人以上連れてくるはずがないので，アイウエオの五国はそれぞれ別々，あいうえおの五国もそれぞれ別々です．
アイウエオの中には10国への通訳（0→10）は混じってませんでした．
あいうえおの中にも 0国への通訳（10→0）はいなかったはずです．
それにまさか自分の国（0→0，10→10）としゃべるための通訳なんか連れて来てるはずもありません．
するとアイウエオあいうえおの中には0国と10国は混じってないことになります．
さて，アイウエオあいうえおの国々が全部違うなんてことがあるでしょうか．
0と10が混じってないので残りは九カ国．
アイウエオあいうえおは全部で十あります．
ってことはつまり必ずどこかで同じ国への通訳がいるということになりますね．
というわけでうまくいきました．
Nが偶数だった場合も同じように示せます．
この方法を使えば、多くても間に２人の通訳がいれば会話できることになります．
◆出題者のコメント。
解答ありがとうございます。
「ただし、他の国で同伴させる通訳者のことはお互いに不明です。」
の表現が曖昧でした。
「他の国で同伴させる通訳者がどこの国の言葉なら理解できるのかは、お互いに知りません。」
と改めました。
ですから、特定の言語を指定する場合はありません。
出題者として意図したのは、「迷子の雄猫さん」の２のケースです。
「多くとも何人の通訳者を経由すれば対話が可能でしょうか？」は、
「対話する代表者と代表者のあいだに入る通訳者の数が最悪(最多)の場合でも何人入れば十分でしょうか？」
の意味です。
できることなら簡単な説明をして下さい。
参加国数をＮ(≧２)ヶ国 と与えているので、開催国が参加国に含まれても含まれなくても解答は一緒です。
また、ある参加国にとっては当然自分の国はＮ(≧２)ヶ国 に含まれています。
また、問題文の裏には次の意味があります。
どの国も別の言葉の通訳者を同伴させ、同じ言葉の通訳者を複数同伴させるような無駄なことはしません。