辺を 1 :
辺を
区分点は30度、60度と45度、45度の内角の2つの直角三角形の作図により簡単にもとまる。
◆宮城県 甘泉法師 さんからの解答。
【問題1】 三角形の場合の答
三角形の面積を1:2に分ける直線を引く方法にはたとえば次のものがある
◆方法a
辺を3等分して、対角と3等分する点をむすべばよい。
なお、3等分する方法は、この「数学の部屋」の図形問題にある。
◆方法b
辺を 1 :![]() −1 に内分する点、2つを結ぶ
−1 に内分する点、2つを結ぶ
辺を ![]() :
:![]() −
−![]() に内分する点、2つを結ぶ
に内分する点、2つを結ぶ
区分点は30度、60度と45度、45度の内角の2つの直角三角形の作図により簡単にもとまる。
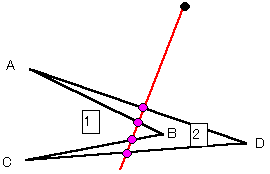
これらで引いた線、あるいは他のやりかたで引いた線のどれでもいいから1本をとり、三角形の周との交点をA,Bとする。
点Aの近くで三角形の周上にある点Cを、同じく点Bの近くで三角形の周上にある点Dをとる。
ただし、周ACおよび周BDの間には三角形の頂点を含まないようにする。
線分ABと線分CDが点Qで交わり線分BCと線分DAが平行であるようにとることができる。
すると△AQC=△BQDなので、直線CDも三角形の面積を1:2に分ける直線になる。
これを連続的に続けていけば、任意に指定された点をとおり、三角形の面積を1:2に分ける直線を引くことが出来る。
【問題2】 四角形の場合の答
4角形ABCDの対角線BCを1:2に内分する点を作図しPとする。
点Pを通り対角線ADに平行な直線が点Dから伸びる四角形の辺と交わる点をQとする。
直線AQは四角形ABCDの面積を1:2に分ける。
直線AQについて、問題1で説明した<<領域間での同じ面積の三角形のトレードによる変換>>を連続的におこなう。
こうして任意に指定された点をとおり、四角形の面積を1:2に分ける直線を引くことが出来る。
【感想】
(1)同じやり方で、凸多角形の面積を任意に指定された比に分ける直線が1本与えられれば、あたえられた任意の点 を通り凸多角形の面積を任意に指定された比に分ける直線を引くことができる。
(2)点が線の上をとおるよう、行きつ戻りつしてだんだん近づくコンピュータ向きのような迂遠な方法です。
もっとエレガントな方法があればいいのですが。
◆愛知県 Y.M.Ojisan さんからの解答。
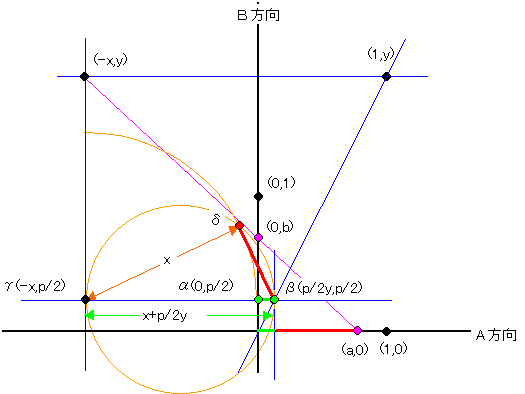
【補題】
一般に三角形をp:(1−p)に分割する場合を考える。
ただし、0≦p≦1は長さ比として幾何学的に作図可能な実数値、ないし既に幾何学的に長さ比として与えられているとする。
三角形を下図の状態になるようにOABとし、外部の点をQとする。
下図の状態に記号付けが可能かどうかは必ずしも自明ではない。
ここでは、最悪O位置を3通り試せばどれか当たるということに留める。
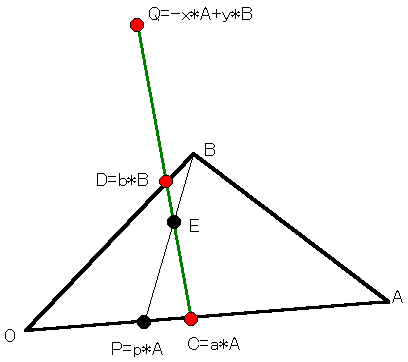
各大文字記号は点Oを原点とするベクトルでもあるとし、その他の点を上図のように定義する。
ここでa,b,x,yは実数値係数である。
△OBP:△BPA=p:(1−p)であるから、
問題は△DBE=△PCEなる点Eを線分PB上に求めることになる。
(△:面積の意味)
さて
△OAB=|A×B|
△OCD=ab|A×B|=ab△OAB=p△OAB
なる関係があり、面積比はベクトルA,Bには拠らない。
つまり、詳細は省略するが、この問題は線形的変形を行って考えても構わない。
即ち、下図で,a,bを求めた値を変形前に適用しても面積比には影響しない。
即ち、
| - | x a | + | y b |
=1,ab=p |
| これを解くと | 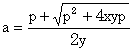 | である。 |
この式を変形すると、
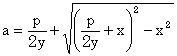 |
であり、作図可能である。 |
| B軸上に点α(0, | p 2 | )をとる。 | p 2 |
は作図可能。 |
| 点β( | p 2y | , | p 2 |
)とする。 |
| αからxの距離に点γ(-x, | p 2 |
)をとる。 |
| この時δとβの距離は | 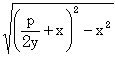 | である。 |
【問題1】
p=1/3は有理数であり、長さ比として幾何学的に作図可能である。
よって、補題により点Qを通り三角形を1:2に分割する線の作図が可能である。
【問題2】
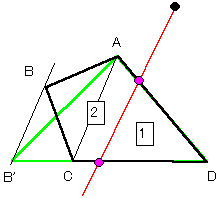
4角形の場合、分割線は必ず4つある辺のうち2辺を通過している。<typeA> 隣接する2辺を通過する場合(下図参照)
この場合は、通過しない2辺を変化させ等積変形して3角形に変形することにより、補題が適用され、面積を1:2に分割できる。
結果として得られた交点が元の4角形上の点であればそれが解である。
延長した部分上の場合は、別のtypeAの組み合わせを試す。
それでもなければ 次のtypeB or Cを試す。
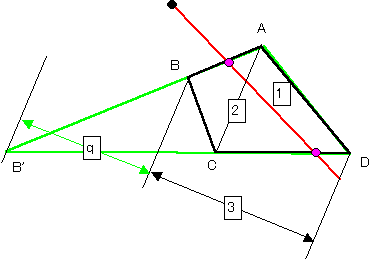
<typeB> 対抗する2辺を通過する場合でこの2辺が平行でない場合。(下図参照)
その2辺をAB,CDとする。
AB,CDを延長した交点をB’とするとき、新たに加わった三角形部分BB'Cの面積と元の4角形の面積の比は、例えば線分ACを底辺とする三角形を考えることにより、下図のように幾何学的な長さの比として作図可能である。
これをq:3とすると、三角形AB'Dをq+2:1に補題により分割すれば良い。
なお、長さ比q+2:1は容易に作図可能である。
typeA同様、得られた交点が元の4角形上であればそれが解である。
そうでなければもう一つのtypeB or Cを試す。
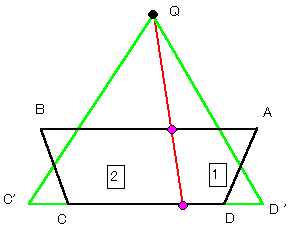
<typeC> 対抗する2辺を通過する場合でこの2辺が平行の場合。(下図参照)
その2辺をAB,CDとする。
BCの中点とQを結んだ直線およびADの中点とQを結んだ 直線とCDを通る直線との交点をそれぞれC',D'とする。
左または右端にできた小さな上下の三角形は各々等面積である。
従って、△QC'D'を1:2に分割するQを通る線分は元の4角形を1:2に分割する。
四角形が凸四角形であれば、以上3type,6ケースの内のどれかに解がある。
凹四角形の場合は不可能なケースがある。
但し2分割の意味を直線の左右とすれば、実質3分割状態で解がある。
しかし、ここで示した補題の方法では作図できない。
【感想】
非常に単純な問題なのに、深いものがあり、良い問題ですね。
私の解は幾何学的というにはかなりこじ付けが強く、綺麗ではありません。
もっとスマートな本当の意味で幾何学的解があるのであろうと思いますが、他の方にお願いせざるを得ません。
◆愛知県 Y.M.Ojisan さんからの解答。
【問題2追加解答】
さきの回答において、凹4角形の場合できない場合があると書いたが、
面積分割比が1:2の場合は凹4角形でも本解答の方法で可能である。
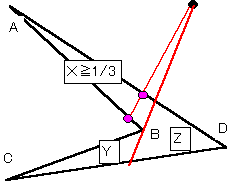
∵ 下図のように分割線を凹点Bを通る臨界状態に引いたときにできる3つの三角形の面積をX,Y,Z
| X+Y+Z=1としたとき、max(X,Y,Z)≧ | 1 3 |
である。 |
従って、何れか最大面積の三角形から1/3を切り取ることが可能である。
例として下図はXが最大の場合である。
| 一般には、0≦p≦ | 1 3 |
or | 2 3 |
≦p≦1 であるとき、 |
【感想】
分割比1:2には必然性があったのですね。すばらしい。
◆宮城県 甘泉法師 さんからの解答。
Y.M.Ojisan さんの解答を拝見して、先の解答では凹四角形の場合を失念していたことに気づき、凹四角形にも適用できる図形的解法を考えました。
どんな三角形についても以下の手順で、面積が同じ直角三角形で直角をはさむ1辺の長さが決まっているもの、を作図することができる。
さて与えられた点を通り、四角形を分割する直線の分割の具合は
(1)直線のどちらかに三角形がある。
(凹四角形なら2個の場合もある)
(2)直線のどちらも四角形である。
のどちらか。
(1)の場合、三角形を「直角三角形」に変形する。
三角形2個の面積の和に等しい「直角三角形」は1と同じ要領でできる。
(2)の場合、四角形を内部をとおる対角線に沿って2つに分けて同じことをする。
こうして、直線の片方にある四角形内部の面積と四角形の面積(の1/3)は、「辺AE」の大小により図で判別できる。
求める直線の片側の面積は直線の角度と増か減か明らかな単調な関数であることから角度をどちらにかえて試行していくかは明らか。
こうして作図だけで、求める直線に任意の精度で近づける。
【感想】
作図だけでできることはできますが、実際手でやることを考えると気が遠くなります。
◆宮城県 甘泉法師 さんからのコメント。
図形の面積を分ける直線の通る点が、図形の外にある場合をこれまで考えてきたが、図形の中にそこを通る直線が図形の面積を題意に分けられないような領域がある。
たとえば三角形の重心を通る直線の面積の分け方は次の式のとおり。
| 1 2 | < | 22 32−22 |
= | 4 5 | ≦ | 小さい方 大きい方 | ≦1 |
領域の境界の形を考えていますがおわかりの方はご教示ください。
◆愛知県 Y.M.Ojisan さんからのコメント。
【Re:甘泉法師 さんからのコメント】
結論だけです。
3角形の場合は、各2辺3組を漸近線とする、所定の面積分割線(点Qを通る必要ない)に接する(=包絡される)3つの双曲線で囲まれた内側です。
図形を線形変換して直角二等辺三角形で考えれば簡単です。
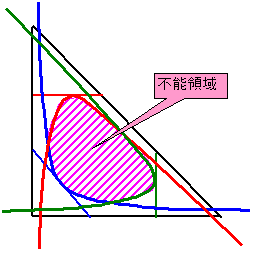
凸4角形の場合は、やはりtypeA,B,Cに分ける必要がありますが、typeCによる境界を除く幾つかの双曲線で囲まれた内側になります。
typeCの境界線はくの字の折れ線ですが、これが表面化することはありません。
凹四角形の場合はtypeA,Bだけですが、とてもややこしい。