◆宮城県 甘泉法師 さんからの解答。
一部だけですがすぐにわかった分だけ送ります。
◆東京都 ぽこぺん さんからの解答。
【解答】
次の (1),(2),(3) の合併図形 (下図の黒実線部)。
(1) 辺 BC の垂直二等分線の,△ABC に含まれない部分 (境界は含まない)。
(2) 点 B における AB の垂線と点 C における AC の垂線との交点を O とするとき,O を中心として辺 AB,AC に接する円周の, △ABC に含まれない部分 (境界は含まない)。
(3) 3 次曲線
4の一部。x3+6x2y+4
xy2+6y3+12
x2+6xy+2
y2+9
x-3y+2
=0
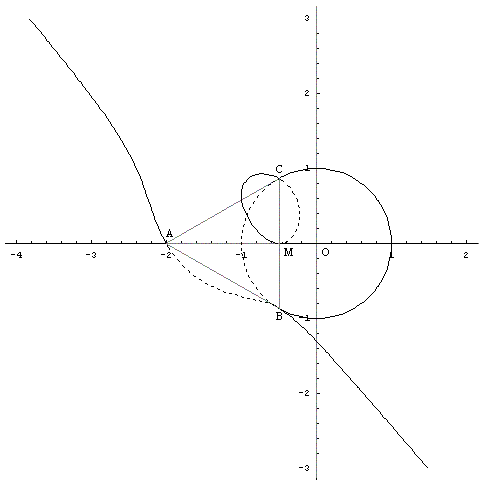
【証明】
(1) 明らか。
(2) 図形 (2) の上の任意の点 D に対して,直線 DA,DM と円周との D でない交点をそれぞれ X,Y とする。
ここで,円 O の半径を r とすると,
| OM = | r 2 | ,OA = 2r となるので下記の補題の条件を満たし, |
したがって,弧 BX = 弧 CY となり,
2 つの弧に対する円周角の間に ∠ADB = ∠MDC が成り立つ。
(点 D が,円周上で △ABC に含まれる部分にある場合には,弧 BX,弧 CY に対する円周角が ∠ADB,∠MDC にはならない。
| ただし,△ABC に含まれる円周上の点 (- | 13 14 | , | 3 14 | ) においては |
| ∠ADB = ∠MDC = | π 2 | になるので条件を満たすが, |
(3) 上図のように座標を定め,
| {( | → DA |
, | → DB |
)/‖ | → DA |
‖‖ | → DB |
‖} | 2 | -{( | → DM |
, | → DC |
)/‖ | → DM |
‖‖ | → DC |
‖} | 2 | = 0 |
y(x2+y2-1)(4と因数分解できる。x3+6x2y+4
xy2+6y3+12
x2+6xy+2
y2+9
x-3y+2
)
この第 3 因数を 0 とおいたものが図形 (3) であり,上図のようなグラフが描けるが,この曲線の詳細な性質はわからなかった。
【補題】
中心 O,半径 r の円 O において,O を端点とする半直線上に
OA・OB = r2 となる 2 点 A,B を取る。
円周上の任意の点 P に対して,直線 AP,BP と円周との (P でない) 交点をそれぞれ X,Y とすると,
∠AOX = ∠AOY である (下図)。
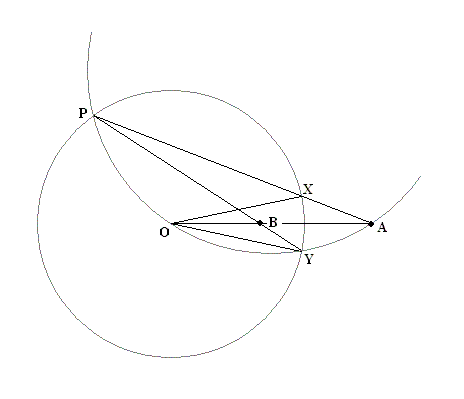
【証明】
弦 PY の円 O に関する反転図形は △OPY の外接円となるが,PY が点 B を通るので,この円は点 A を通る。
| したがって,∠AOY = ∠APY = | 1 2 | ∠XOY が成立する。 |
(証明終)
【感想】
補題は有名な命題なのでしょうか?
補題が初等幾何で証明できたときには,これで解決した!と喜んだのですが,残った (3) の 3 次曲線がどうしても解明できませんでした。
既知の正葉線などの曲線と結び付けようと四苦八苦したのですが,うまくいかないので,とりあえずこのままにします。
甘泉法師さんの(イ)は (3) に含まれます。
◆出題者のコメント
ご解答ありがとうございます。
ぽこぺんさんの解答で正解でしょう。
6線分からなる軌跡が求める解です。
問題は単純ながら、このように3次曲線が解にでてきます。
この問題は∠ADB=∠ADCなる点Dの軌跡は?という問題の変形でした。
こちらは4線分からなる軌跡となります。
本問題のように替えた場合恐ろしく難しい問題となります。
私もこの3次曲線の性質がわからず出題してみることにしました。
ぽこぺんさんの軌跡(2)が解であると真っ先に気が付いたのですが、それにしてもよく気が付きましたね。
【補題】は有名な事実だとは思いますが、これと本問題を結びつける解答があるとは思いませんでした。
どなたかこの3次曲線の幾何学的性質がわかりましたらご一報ください。
◆東京都 ぽこぺん さんからの解答。
【この 3 次曲線についての考察】
[1] 本問の 3 次曲線の式,
において y = √3 y' とおけば,4√3 x3 + 6x2 y + 4√3 xy2 + 6y3 + 12√3 x2 + 6 xy + 2√3 y2 + 9√3 x - 3y + 2√3 = 0 …… (*)
となる。さらに,4x3 + 6x2y' + 12xy'2 + 18y'3 + 12x2 + 6xy' + 6y'2 + 9x - 3y' + 2 = 0
| x | = | 1 ─ 98 | (15u - 75v - 91) | |
| y' | = | 3 ─ 98 | (-15u + 5v + 7) | |
| u3 + v3 - u2 + uv - v2 - | 16 ─ 25 | u - | 39 ─ 25 | v = 0 …… (**) | |||||
に対して,上記と同様の回転・裏返し・伸縮・平行移動 (自由度 5) を適用すると (縮退する場合を除き),a x3 + b x2y + c xy2 + d y3 + e x2 + f xy + g y2 + h x + i y + j = 0
という形に直すことができる。 ただし,(1) uv の項を消去することはできず,(2) u の項と v の項の係数を等しくすることもできない。u3 + v3 + E u2 + F uv + E v2 + H u + I v = 0
[2] いま,(**) において一次の項の係数を共に -1 とすると,
は下のように直線 v = u に関して対称なグラフとなる。u3 + v3 - u2 + uv - v2 - u - v = 0 …… (***)
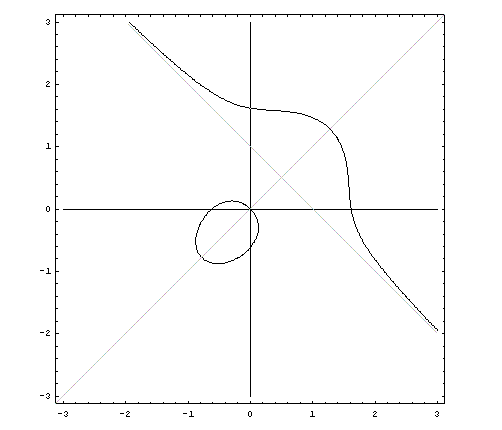
(***) の漸近線は,これと交点を持たない直線である。
したがって,それを v = mu + n とおいて両式から v を消去すると,方程式
が得られるが,これが実数解を持つことはない。(m + 1)(m2 - m + 1) u3 + (3m2n - m2 + m - 1) u2 + (3mn + m + 1)(n - 1) u + n(n² - n - 1) = 0
となり, n ≠ 1 ならば 2 次方程式となるが, n = 1 ならば解を持たない。3(n - 1) u2 - 3n(n - 1) u + n(n2 - n - 1) = 0
すなわち9n2(n - 1)2 - 12n(n - 1)(n² - n - 1) ≧ 0
| 1 - √17 2 |
≦ n ≦ 0 または 1 < n ≦ | 1 + √17 2 | |||
のように得られる。u = -v + 1
これに対して,(*) のグラフは模式的に描くと
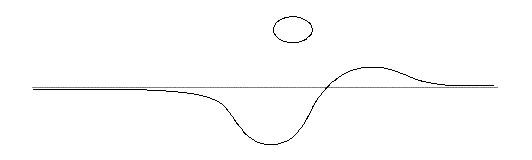
のようになっている。
これを確かめるために,(*) と y = mx + n とを連立させて y を消去し,3 次方程式にならない場合を考えると,
| m = - | 2√3 3 | ||
となる。この方程式の解の個数を n の値によって分類すると次の表のようになる:2(21n + 16√3)x2 - 3(8√3 n2 + 2n - 11√3)x + 3(6n3 + 2√3 n2 - 3n + 2√3) = 0
| n の値 | … | -7√3 - 3√(15+8√3) 12 | … | -16√3 21 | … | -7√3 - 3√(15-8√3) 12 | … | -7√3 + 3√(15-8√3) 12 | … | -7√3 + 3√(15+8√3) 12 | … |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 近似値 | … | -2.35332 | … | -1.31966 | … | -1.27771 | … | -0.743016 | … | 0.332591 | … |
| 解の個数 | 0 | 1 | 2 | 1 | 2 | 1 | 0 | 1 | 2 | 1 | 0 |
したがって,漸近線は 1 次方程式になる場合,すなわち
| n = - | 16√3 21 | ||