◆愛知県 Y.M.Ojisan さんからの解答。
【問題1証明】
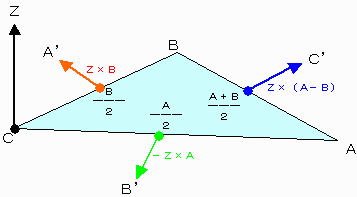
C =(0,0,0) A= (A1, A2, A3) B= (B1, B2, B3) とする。
Zk=z*εijk*Ai*Bj [△ABCに直交する任意長ベクトルほどの意味]
を用いて条件(1)(2)(3)を満たすA',B',C'は次のように表される。
A'i=Bi/2+εijk*Zj*Bk
B'i=Ai/2‐εijk*Zj*Ak
C'i=(Ai+Bi)/2+εijk*Zj*(Ak-Bk)

CC'とAA'の交点Pはs,tを未知パラメータとして
Pi=s*C'i=Ai+t*(A'i-Ai)
両辺に(A'j-Aj)を外積しZiとの内積をとると、
s=εijkZi*Aj*(A'k-Ak)/εijkZi*C'j*(A'k-Ak)
一方、CC'とBB'の交点Qはs',t'を未知パラメータとして
Qi=s'*C'i=Bi+t'*(B'i-Bi)
両辺に(B'j-Bj)を外積しZiとの内積をとると、
s'=εijk Zi*Bj*(B'k-Bk)/εijk Zi*C'j*(B'k-Bk)
sの分子は
εijk Zi*Aj*(A'k-Ak)
=εijk Zi*Aj*A'k=εijk Zi*Aj*(Bk/2+εkpq*Zp*Bq )
=1/2*εijk Zi*Aj*Bk +εijkεpqkZi*Zp*Aj*Bq
=1/2*εijk Zi*Aj*Bk + Zi*Zi*Aj*Bj- Zi*Zj*Ai*Bj
(εijkεpqk=δipδjq−δiqδjp を用いた)
同様に s'の分子は
=1/2*εijk Zi*Bj*Ak−Zi*Zi*Aj*Bj+Zi*Zj*Bi*Aj
=-1/2*εijk Zi*Aj*Bk−Zi*Zi*Aj*Bj+Zi*Zj*Ai*Bj
従ってs'の分子=−sの分子である。
sの分母+s'の分母は
εijk Zi*C'j*(A'k-Ak)+εijk Zi*C'j*(B'k-Bk)
=εijk Zi*C'j{ Bk/2+εkpq*Zp*Bq-Ak+Ak/2-εkpq*Zp*Aq-Bk}
=-εijk Zi*C'j{(Ak+Bk)/2+εkpq*Zp(Aq-Bq)}
=-εijk Zi*C'j*C'k
=0
であり sの分母=−s'の分母 である。
即ちs=s' であり、P=Qである。
【PS】
tensorさんの問題なのでテンソル使ってみました。
重心と垂心が統一されているところが興味深いです。
内外心も大統一されると面白いのですが。
◆出題者のコメント。
Y.M.Ojisan さん解答ありがとうございます。
テンソルで来るとは、まったく予想外でした。
思いっきり平面幾何の問題なのですが(^^;;
証明は…計算が激しいですね。
ともあれ、確認しました。間違いは無いようです。
(Einsteinの記法なのに添え字が被ってるというツッコミは置いといて。)
εijk Zi*Aj*Bk = det(Z,A,B)
等を使って幾何的に考えると、もう少しスッキリ証明できるかもしれません。
これ以上書くと【問題2】を解いてしまいそうなのでやめますが。
出題してから気付いたのですが(出題前にチェックしなかったのは申し訳ないですm(__)m)、
岩波の幾何学大辞典に【問題1】の証明が載っているので参考にして下さい。
まだ解けてない方も、できれば独自の証明を考えていただきたいです。
あと、残りの問題も楽しんでください。
◆愛知県 Y.M.Ojisan さんからの解答。
【問題2証明】
三角形ABCの内心を原点とし、内接円の半径を1とする座標をとり、点A,B,Cの座標を定数β、γを用いて次のように表します。
点Aの座標の導出は省略。
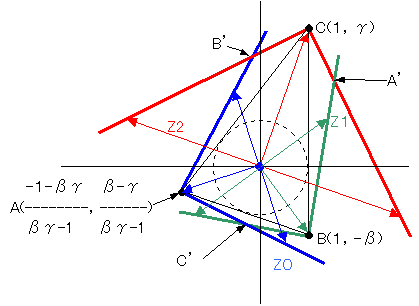
以降A,B,C等はベクトルと考えます。
A,B,Cに直交する任意長ベクトルをZ0,Z1,Z2とします。
即ち90度回転行列をRとして、
Z0=za*R*A,Z1=zb*R*B,Z2=zc*R*C,
ここでza,zb,zcは任意実数値。
すると条件を満足するA’,B’,C’はそれぞれ
B→Z1とC→-Z2, C→Z2とA→-Z0, A→Z0とB→-Z1の交点です。
即ち次の線形方程式が導出されます。
ここでs0,s1,s2,s0’,s1’,s2’は未知数です。
A’=B+s0(Z1-B)=C+s0’(-Z2-C)
B’=C+s1(Z2-C)=A+s1’(-Z0-A)
C’=A+s2(Z0-A)=B+s2’(-Z1-B)
これらは線型方程式ですから容易に解くことができます。
つぎにA→A’ と B→B’の交点をU A→A’ と C→C’の交点をVとするとき
それらはu1,u2,u1’u2’を未知数として次の線型方程式を解けば求めることができます。
U=A+(A’-A)*u1=B+(B’-B)*u1’
V=A+(A’-A)*u2=C+(C’-C)*u2’
U=VであるかどうかはQ=u1-u2が0であればよいことになります。
ところで、A,B,Cはβ,γの整数係数有理多項式であり、
従ってZ0,Z1,Z2はβ,γ,za,zb,zcの整数係数有理多項式です。
以降Qを得るまで、全て線形方程式ですから途中経過も含め得られたQもまた、β,γ,za,zb,zcの整数係数有理多項式です。
最終的に得られるであろう値が0であること、多項式であること、陽に解けていることから、因数分解や約分の必要がなく、数式処理のなかでも最も簡単な問題です。
そこで数式処理(というよりは数値計算)でこのQ値が0であることを確認しました。
以下に作成したプログラム(VC++ Console Application)と出力を添付します。
実際のプログラムでは、約分しないことによる分母の爆発を抑えるために
全体に(βγ-1)倍したところから始め、途中A’-A等の分母をu*に繰り込んで1にしています。
このようにして得られたu1値は39項/289項の大きさですが、
実際には(1+β2)(βγ-1) (1+γ2)などで約分可能かもしれません。
なお、アルゴリズミックな互除法による約分により無用な爆発は回避することも可能です。
ヘッダ: Main.h Tankou.h Takou.h Yuuri.h
ソース: Main.cpp Tankou.cpp Takou.cpp Yuuri.cpp
出力 : out.txt
【ソフト解説】
なお、A’,B’,C’は次のように計算されます。
β、γを定数とみるとza,zb,zcの双一次整数係数有理多項式になっています。
おまけの証明(幾何的には不可能とか?)に利用できるかも。
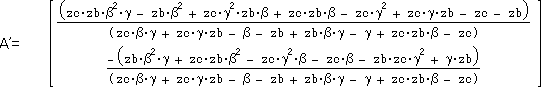
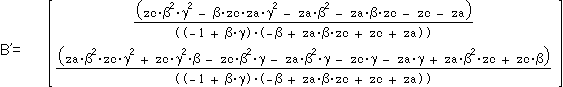
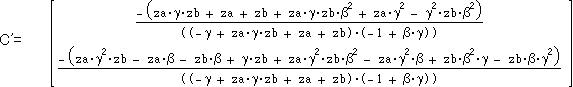
【PS】
今回は私のテーマであるAnaConism[無理やり計算機とでも訳しますか、私的造語です]で解いてみました。
結果は意外と項数が少なく、39項/289項ぐらいなので、プログラムを作っているより手計算のほうが速かったかもしれませんが、大抵間違うでしょうね。
十分に楽しませていただきました。
問題1のミスご指摘ありがとうございます。
sとs'のところですね。^^“
(正) s=εijkZi*Aj*(A'k-Ak)/εpqrZp*C'q*(A'r-Ar)
◆三重県 いわし さんからのコメント。
[問題2]の△ABCの内心をIとおくと、AB',AC'はAIに関して対称、などとなっていますが、
http://www.cut-the-knot.org/Generalization/fermat_point.shtml
によると、Iは平面上の任意の点Pでよいようです。
つまり、AB',AC'がAPに関して対称、などとなるようにA',B',C'を定めれば、AA',BB',CC'は共点となります。
射影幾何による証明が載っています。
実験もできて、おもしろいです。
◆出題者のコメント。
Y.M.Ojisan さん解答ありがとうございます。
今度はさすがに座標を使った解法では来ないだろうと予想していましたが、プログラムを組まれては形無しですね。
プログラムの検証は私には手に負えないですが、演算子を定義したりとしっかり書いてあるようなので安心です。
証明方針は堅実で文句なしです。
内心を原点とするなど工夫が見られますが、計算結果を見る限り手計算では厳しいでしょう。
【おまけ】については、
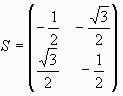 (S3=1)
(S3=1)
A' + S*B' + S2*C' = 0 or A' + S2*B' + S*C' = 0⇔ A'B'C'は正三角形
よりza,zb,zcの方程式が求まります(大変なので計算していませんが)が、これを幾何的な性質に翻訳するのは難しそうです。
まあ、幾何的に綺麗に書けるとは限りませんが期待はしたいです。
いわし さんコメントありがとうございます。
海外のサイトに出ていましたか。調査力不足で申し訳ありません。
典型的な射影幾何の証明ですね。まったく知りませんでした。
というか、内心に関して対称になっていることも気付きませんでした(爆
誤解が無いように補足しますと、上のページに載っている射影幾何の定理は、
「T(直線AP)=直線AP, T(直線AB)=直線AC, T(直線AC)=直線ABなる射影変換Tに対して、
T(直線AB')=直線AC'等となるようにA',B',C'を定めれば、AA',BB',CC'は1点で交わる。」
と言っているようなので、P≠Iの場合、直線AB'と直線AC'は直線APを軸として対称になるとは限りません。
勿論、射影幾何を用いなくても反例は容易に見付かります。
ちなみに、私の用意している解答は三角関数と中学生程度の知識があれば容易に理解できるものです。
もっと簡単にできるぞ、という方は是非投稿してください。
◆神奈川県 諏訪 冬葉 さんからの解答。
【問題1】
仮定より
∠A'BC=∠A'CB=∠B'AC=∠B'CA=∠C'AB=∠C'BA
これをθと置く
AA' と BC の交点を D
BB' と CA の交点を E
CC' と AB の交点を F
とする。
BD:DC
=△ABD:△ACD
=△A'BD:△A'CD
=△AA'B:△AA'C
| = | (AB)(A'B)sin(B+θ) 2 | : | (AC)(A'C)sin(C+θ) 2 |
同様に
CE:AE=(BC)sin(C+θ):(AB)sin(A+θ)
AF:BF=(AC)sin(A+θ):(BC)sin(B+θ)
| よって | BD CD | * | CE AE |
* | AF BF |
=1 |
チェバの定理より三本の直線は一点で交わる。
ちなみにθのおもな値で求まる点は
0:Centroid
30:Napoleon point
45:Vectan Point
60:Fermat Point
90:Orthocenter
といいます。
【問題2】
DEF は問題1の解答と同様に定義する
∠BAC'=∠CAB'=α
∠CBA'=∠ABC'=β
∠ACB'=∠BCA'=γ
とおく。
問題1と同様に
BD:DC
=△AA'B:△AA'C
| = | (AB)(A'B)sin(B+β) 2 | : | (AC)(A'C)sin(C+γ) 2 |
CE:AE=(BC)sin(C+γ)sinα:(AB)sin(A+α)sinγ
AF:BF=(AC)sin(A+α)sinβ:(BC)sin(B+β)sinα
よって、チェバの定理より三直線は一点に交わる。
◆出題者のコメント。
諏訪 冬葉 さん解答ありがとうございます。
【問題1】【問題2】共に見事正解です。
チェバの定理(の逆)を使って、対称性を維持したまま綺麗に解かれています。
特殊な場合で名前の付いてるものは、並べてみると結構ありますね。
因みに、【問題2】でα+β+γ=πの場合も綺麗な性質があります。
私の用意していた解答も同様ですが、この方法の欠点(?)は、
図形的な意味が分かり難いところだと思います。
別証や【おまけ】の回答も待ってます。