『正三角形の存在』解答

◆滋賀県　一平 さんからの解答。

【問題１】

ｘ軸，直線 y=1，直線 y=c (c＞1)を l1， l2， l3とする。
平行な３直線を l1， l2， l3として，一般性を失わない。

今，A(0,0)を通る直線 y=x／m　(m＞0)を考え，
ｌ2との交点を B(m，1)とする。

点Bを原点を中心に６０°回転して、直線 l3と交わったとしよう。

これは、回転による１次変換で求めることができ、ｙ座標がcであることから、

m
2		 + 1
―
2		 =c

これをｍについて解くと、
m= 2c-1

よってＢ，Ｃの座標は

B( 2c-1
 ，1)，C( c-2
 ，c)

となる。

逆にこのようなA，B，CはAB=BC=CAを満足する。
よって、３点Ａ，Ｂ，Ｃは正三角形を作る。

◆静岡県　ヨッシー さんからの解答。

【問題２】

図のように、３本の平行線を、
l1,l2,l3 とし、l2 は l1 と l3 の間にあるものとします。

  1. l1 をｘ軸、l3 を 直線ｙ＝１　に見立て、
    ｙ軸および、直線ｙ＝２を垂線の作図により描きます。

  2. 点（０，２）から、傾き−の直線を引きます。
    直線ｙ＝２と６０°をなす直線として作図します。

  3. この直線と、l2 の交点Ａが、求める正三角形の頂点の一つであり、
    点Ａを中心とし、ＡＯを半径とする円を描けば、l3 上の頂点が求められます。
説明：

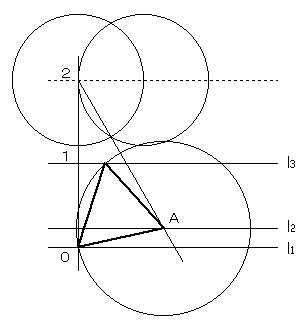
直線 l3 上に、点Ｂ(m,1)をとります。
この点を原点周りに−６０°（６０°でも良い）回転させた点をＣとすると、
△ＯＢＣは正三角形になります。

点Ｃの座標は

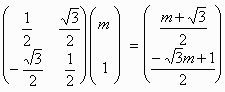
x= m+
2

y= -m+1
2

として、m を消去すると

y=-x＋2 となり、
点Ｃは、直線 y=-x＋2 上にあることになり、

上記の作図で正三角形の各頂点を求めることができます。

◆静岡県　ヨッシー さんからのコメント。

よく考えたら、直線 l3 上の任意の点を原点周りに±６０°回転させた点が正三角形の第３の点になるので、
直線 l3 を原点周りに±６０°回転させた直線になるのは、当たり前ですね。

　『正三角形の存在』へ

　数学の部屋へもどる