『３つの正三角形』解答

◆静岡県　ヨッシー　さんからの解答。

Ｏを原点とし、
ＯＡ＝ＯＢ＝４ａ
ＯＣ＝ＯＤ＝４ｂ
ＯＥ＝ＯＦ＝４ｃ
　（ａ＞０，ｂ＞０，ｃ＞０）とし、
ＯＡ、ＯＣ、ＯＥの角度を、α、β、γとすると、各点の座標は、

Ａ：（４ａcosα，４ａsinα）

Ｂ：（４ａcos(α+π/3)，４ａsin(α+π/3)）
　＝（２ａcosα―２ａsinα，２ａsinα＋２ａcosα）

Ｃ：（４ｂcosβ，４ｂsinβ）

Ｄ：（４ｂcos(β+π/3)，４ｂsin(β+π/3)）
　＝（２ｂcosβ―２ｂsinβ，２ｂsinβ＋２ｂcosβ）

Ｅ：（４ｃcosγ，４ｃsinγ）

Ｆ：（４ｃcos(γ+π/3)，４ｃsin(γ+π/3)）
　＝（２ｃcosγ―２ｃsinγ，２ｃsinγ＋２ｃcosγ）

Ｌ：（ａcosα―ａsinα＋２ｂcosβ，ａsinα＋ａcosα＋２ｂsinβ）

Ｍ：（ｂcosβ―ｂsinβ＋２ｃcosγ，ｂsinβ＋ｂcosβ＋２ｃsinγ）

Ｎ：（ｃcosγ―ｃsinγ＋２ａcosα，ｃsinγ＋ｃcosγ＋２ａsinα）

以下、点Ｍを点Ｌのまわりにπ／３回転させると、点Ｎに一致することを示す。

△ＬＭＮを点Ｌが原点になるように平行移動した三角形を△ＯＭ'Ｎ'とすると、
点Ｍ'の座標は、点Ｍの座標から点Ｌの座標を引いて、

Ｍ'：（−ａcosα＋ａsinα−ｂcosβ―ｂsinβ＋２ｃcosγ，−ａsinα−ａcosα−ｂsinβ＋ｂcosβ＋２ｃsinγ）

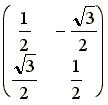
によって、回転させた点をＮ''とすると、その座標は

Ｎ''：１／２（−ａcosα＋ａsinα−ｂcosβ―ｂsinβ＋２ｃcosγ＋√３ａsinα＋３ａcosα＋ｂsinβ−３ｂcosβ−２ｃsinγ，−ａcosα＋３ａsinα−ｂcosβ―３ｂsinβ＋２ｃcosγ−ａsinα−ａcosα−ｂsinβ＋ｂcosβ＋２ｃsinγ）
＝１／２（２ａcosα＋２ａsinα−４ｂcosβ＋２ｃcosγ−２ｃsinγ，−２ａcosα＋２ａsinα―４ｂsinβ＋２ｃcosγ＋２ｃsinγ）
＝（ａcosα＋ａsinα−２ｂcosβ＋ｃcosγ−ｃsinγ，−ａcosα＋ａsinα―２ｂsinβ＋ｃcosγ＋ｃsinγ）

Ｎ'：（ａcosα＋ａsinα−２ｂcosβ＋ｃcosγ−ｃsinγ，−ａcosα＋ａsinα―２ｂsinβ＋ｃcosγ＋ｃsinγ）

以上より、点Ｍを点Ｌを中心にπ／３回転した点は点Ｎに一致し、
△ＬＭＮは正三角形である。

ただし、△ＬＭＮが存在しない場合（３つの正三角形が完全に重なる場合など）は除く。

◆宮城県　アンパンマン　さんからの解答。

問題の図をつかって説明します。

v(XY)=vector XY とします。

v(ML)
=v(MO)+v(OL)
=(v(EO)+v(DO))/2+(v(OC)+v(OB))/2
=(v(EO)+v(DC)+v(OB))/2

同様に

v(NM)=(v(AO)+v(FE)+v(OD))/2,
( =(v(EO)+v(DC)+v(OB))/2 with 120 degrees rotation)

つまり｜v(ML)｜＝｜v(NM)｜with the angle between ML and NM = 60 degrees.

なので△MNL＝正三角形です。

◆静岡県　村松　芳子　さんからのコメント。

この問題は図形シリーズの『正三角形？ Part2』の問題２と同じです。
角度だけで解く方法で解答しておきましたので、ご覧ください。

　『３つの正三角形』へ

　数学の部屋へもどる