亀柺愊偼壗暘偺偄偔偮丠亁
亀柺愊偼壗暘偺偄偔偮丠亁夝摎
仧愮梩導丂Hiroshi Maki丂偝傫偐傜偺夝摎丅
丂儀僋僩儖傪巊偭偰堦斒夝傪峫偊傑偟偨丅
暥拞偺嫮挷暥帤偼儀僋僩儖傪昞偟傑偡丅
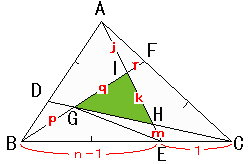 俙俛亖倐丆俙俠亖們偲偡傞丅
俙俛亖倐丆俙俠亖們偲偡傞丅
俙俬丗俬俫丗俫俤亖倞丗倠丗倣乮俰亄俲亄倣亖侾乯丆
俛俧丗俧俬丗俬俥亖倫丗倯丗倰乮倫亄倯亄倰亖侾乯
偲偟偰丏丏丂丂乮俧俤偼曗彆慄偱偡乯
俙俬儀僋僩儖傪2偮偺曽朄偱昞偟傑偡丅
丂侾丏俙俬亖倞俙俤
丂丂丂丂丂亖乮倞乛値乯倐亄倞乮侾亅侾乛値乯們
丂俀丏俙俬亖俙俥亄俥俬
丂丂丂丂丂亖乮侾乛値乯們亄
倰乮倐亅乮侾乛値乯們乯
丂丂丂丂丂亖倰倐亄乮侾乛値乯乮侾亅倰乯們
侾丆俀偺倐丄們奺儀僋僩儖偺惉暘偼摍偟偄偐傜
丂丂倞乛値亖倰
丂丂倞乮侾亅侾乛値乯亖乮侾乛値乯乮侾亅倰乯
楢棫曽掱幃傪夝偄偰丄
丂丂倞亖値乛乮値俀亅値亄侾乯
丂丂倰亖侾乛乮値俀亅値亄侾乯
倫丄倯丄倰偺斾偼壖掕偩偗偳丄尒曽傪曄偊偰傗傟偽丄倞丄倠丄倣偲摨偠偵側傞偺偱
丂丂倫丗倯丗倰亖倞丗倠丗倣
偡側傢偪
丂丂倣亖倰亖侾乛乮値俀亅値亄侾乯
丂丂倠亖侾亅倞亅倣亖値乮値亅俀乯乛乮値俀亅値亄侾乯
偙傟偱倞丄倠丄倣慡偰弌偦傠偭偨偺偱丄仮俬俧俫偺柺愊傪寁嶼偱偒傞丅
仮俙俛俠偺柺愊傪侾偲偟偰丄弴偵彫偝偄嶰妏宍傪媮傔傞梫椞偱丏丏
仮俬俧俫亖乮値亅侾乯乛値亊乮倠亄倣乯亊倠乛乮倞亄倠乯
亊倠乛乮倠亄倣乯
丂丂丂丂丂丂丂仮俙俛俤丂丂丂仮俬俛俤丂丂丂丂仮俬俧俤丂丂丂丂仮俬俧俫
丂丂亖乮値亅俀乯俀乛乮値俀亅値亄侾乯丂丒丒栤俀偺夝
亂栤戣侾亃丒丒丒丂値亖俁傪忋幃偵戙擖偟偰丂仮俬俧俫亖侾乛俈
亂栤戣俀亃丒丒丒丂乮値亅俀乯俀乛乮値俀亅値亄侾乯
亂栤戣俁亃丒丒丒丂惉棫
亂栤戣係亃丒丒丒丂惉棫
丂俀侽擭傎偳慜偺婰壇傪屇傃妎傑偟偮偮丄栥乆偲峫偊傑偟偨丅
奜愊傪巊偭偰傕偭偲僗儅乕僩偵偱偒傞偺偐側丠
亂僐儊儞僩亃
丂側傞傎偳丄慛傗偐側徹柧偱偡偹丅
拞妛峑揑側傗傝曽傛傝傕尒捠偟偑偒偔偺偑丄偄偄偱偡偹丅
巹傕媣偟傇傝偵儀僋僩儖傪巚偄弌偟傑偟偨丅
仧戝嶃晎偺崅峑惗丂戝怷丂崉偝傫偐傜偺夝摎丅
亙栤戣侾亜偲亙栤戣俁亜
仮俙俛俥亄仮俙俠俤亄仮俢俛俠亖仮俙俛俠傛傝
仮俬俧俫亖仮俙俬俥亄仮俠俤俫亄仮俛俢俧
丂儀僋僩儖俛俫
亖倲儀僋僩儖俛俙亄乮侾亅倲乯儀僋僩儖俛俤
亖乮侾亅倱乯儀僋僩儖俛俢亄倱儀僋僩儖俛俠
儀僋僩儖俛俤亖俀乛俁儀僋僩儖俛俠
儀僋僩儖俛俢亖侾乛俁儀僋僩儖俛俙
傛偭偰 倲亖侾乛俈偩偐傜 仮俫俤俠亖侾乛俈仮俙俤俠
傛偭偰 仮俫俤俠亖侾乛俀侾仮俙俛俠
摨條偵 仮俧俢俛亖仮俙俬俥亖侾乛俀侾仮俙俛俠
傛偭偰 仮俬俧俫亖仮俙俬俥亄仮俠俤俫亄仮俛俢俧亖侾乛俈仮俙俛俠
偙傟偼亙栤戣俁亜偱傕偄偗傞偲巚偆丅
亙栤戣俀亜偲亙栤戣係亜
仮俙俛俥亄仮俢俛俠亄仮俙俤俠亖俁乛値仮俙俛俠偩偐傜
丂仮俬俧俫
亖仮俙俛俠亅俁乛値仮俙俛俠亄仮俙俥俬亄仮俢俛俧亄仮俫俤俠
亖乮値亅俁乯乛値仮俙俛俠亄俁仮俫俤俠
仮俫俤俠傪忋偺傛偆偵媮傔傞偲
仮俫俤俠亖侾乛乮値俁亅値俀亄値乯仮俙俛俠
傛偭偰仮俬俧俫亖乮値亅俁乯乛値亄俁乛乮値俁亅値俀亄値乯
偙傟偼亙栤戣係亜偱傕偄偗傞偲巚偆丅
仧婒晫導偺拞妛峑俁擭惗丂傕偭偪丂偝傫偐傜偺夝摎丅
亂栤戣侾亃
摎偊丂侾乛俈
丂傑偢丆俤傛傝丆俛俥偵暯峴側捈慄傪堷偒俙俠偲偺岎揰傪俰偲偡傞丅
偦偙偱俙俥丗俥俠亖侾丗俀丂乧丂嘆
俛俤丗俤俠亖俀丗侾丂仺丂俥俰丗俰俠亖俀丗侾丂乧丂嘇
嘆丆嘇傛傝丂俙俥丗俥俰亖俁丗係
傛偭偰仮俙俛俤丗仮俙俤俠亖俀丗侾 仺 仮俙俛俤亖仮俙俛俠亊俀乛俁
傑偨丆仮俙俛俬丗仮俬俛俤亖俁丗係 仺 仮俙俛俬亖仮俙俛俤亊俁乛俈
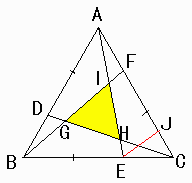 丂
丂
偟偨偑偭偰仮俙俛俬亖仮俙俛俠亊俀乛俈
丂
摨條偵偟偰峫偊傞偲
仮俙俛俬亖仮俠俛俧亖仮俙俫俠亖仮俙俛俠亊俀乛俈
傛偭偰丂仮俬俧俫亖乮侾亅俀乛俈亊俁乯亊仮俙俛俠亖侾乛俈亊仮俙俛俠
亂僐儊儞僩亃
丂崱傑偱崅峑偺抦幆傪巊偭偨夝摎偟偐側偐偭偨偺偱偡偑丄曗彆慄堦杮偱夝寛偟偨偺偑偡偽傜偟偄偱偡丅
傕偪傠傫惓夝偱偡丅
柺愊斾偺栤戣偵姷傟偰偄傞偺偱偟傚偆偑丄夝摎偑戝曄暘偐傝傗偡偔彂偄偰偁傝傑偡偹丅
偤傂丄俀栤栚傕夝偄偰偔偩偝偄丅
仧婒晫導偺拞妛峑俁擭惗丂傕偭偪丂偝傫偐傜偺夝摎丅
亂栤戣俀亃
栤戣俀偺摎偊偑弌傑偟偨偺偱憲傝傑偡丅
| 摎偊丂 |
乮値亅侾乯乮値亅係乯亄値
乗乗乗乗乗乗乗乗乗乗乗乗
値亄乮値亅侾乯2
|
俤傛傝俛俥偵暯峴慄傪堷偒丄俙俠偲偺岎揰傪俰偲偡傞丅
俙俥丗俥俠亖侾丗値亅侾丆俥俰丗俰俠亖値亅侾丗侾傛傝丄
俙俥丗俥俰亖値丗乮値亅侾乯2
傛偭偰丄
仮俙俛俤丗仮俙俠俤亖値亅侾丗侾
丂丂丂伀
仮俙俛俤亖乮値亅侾乯乛値亊仮俙俛俠
仮俙俛俬丗仮俬俛俤亖値丗乮値亅侾乯2
丂丂丂伀
仮俙俛俬亖値乛乮値亄乮値亅侾乯2乯亊仮俙俛俤
偟偨偑偭偰丄
| 仮俙俛俬亖 |
値亅侾
乗乗乗乗乗乗乗乗
値亄乮値亅侾乯2
| 亊仮俙俛俠 |
摨條偵偟偰峫偊傞偲丄
仮俙俛俬亖仮俠俧俛亖仮俙俫俠
| 亖 |
値亅侾
乗乗乗乗乗乗乗乗
値亄乮値亅侾乯2
| 亊仮俙俛俠 |
傛偭偰
丂仮俬俧俫
| 亖乮侾亅 |
値亅侾
乗乗乗乗乗乗乗乗
値亄乮値亅侾乯2
| 亊俁乯亊仮俙俛俠 |
| 亖 |
乮値亅侾乯乮値亅係乯亄値
乗乗乗乗乗乗乗乗乗乗乗乗
値亄乮値亅侾乯2
| 亊仮俙俛俠 |
栤戣俁丆係傕惓嶰妏宍偺惈幙傪棙梡偟偰偄側偄偺偱丄惉傝棫偮偲巚偄傑偡丅
栤戣侾偺摎偊傪嶲峫偵偟偰峫偊傜傟偨偺偱丄妝偱偟偨丅
峫偊曽師戞偱丄杔偨偪拞妛惗偵傕夝偗偰偟傑偆偺偼晄巚媍偱偡偹丅
偙傟偐傜傕偙傫側妝偟偄栤戣傪偍婅偄偟傑偡丅
亂僐儊儞僩亃
丂姰帏側夝摎偱偡丅
妋偐偵堦斒偺嶰妏宍偱傕摨條偵徹柧偱偒傞偲巚偄傑偡丅
偨偩暘巕偼乮値亅侾乯乮値亅係乯亄値亖値2亅係値亄係
偱偡偐傜乮値亅俀乯2偲捈偟偨曽偑旤偟偄偐傕偟傟傑偣傫偹丅
丂亀柺愊偼壗暘偺偄偔偮丠亁傊
丂悢妛偺晹壆傊傕偳傞
 俙俛亖倐丆俙俠亖們偲偡傞丅
俙俛亖倐丆俙俠亖們偲偡傞丅 丂
丂