a=
a=e1/eのときb=eとあらわせる。
◆群馬県 杉田 さんからの解答。
【問題1】
| f(x)の微分、 | df dx | の符号により増減を調べる。 |
| df dx | = | x1/x-1 x | - | x1/x log x x2 |
| =x1/x-2 (1-log x) |
| = | f(x) x2 | (1-log x) |
正数のべき乗は正であるから、
| x>0でf(x)>0, | f(x) x2 | >0である。 |
従って、(1-log x)の符号を調べれば、f(x)の増減がわかる。
log x は単調増加関数であり、log e=1 であるから、f(x)は、
0<x<e のとき増加
x>eのとき減少
x=eで極大(x>0なら最大)
となる。
【問題2】
数列が収束するためには、n→∞で、n+1項とn項が極限値sに等しくなる、
すなわち、以下の等式を満たす必要がある。
s=as ----(2)
a>0であるから、以下のように変形できる。
s1/s=a
問題1より、上式左辺のs>0における最大値は、
sにeを代入して、e1/eとなる。
いま、a>e1/eであるから、(2)式を満たすs(>0)が存在しないことがわかる。
またa>0であるから極限値はs>0である必要がある。
従って数列は収束しない。
次に発散することを示す。
x≧1でax>x であれば、数列は常に増加する。
(an+1>an)
そこで、g(x)=ax-xの符号を検討する。
まず、g(1)=a-1>0である。
さらに、 ax=xとなることはなく、
g(x)が連続であることから、g(x)>0がいえるので、数列が常に増加することが示された。
数列は常に増加して、極限値を持たないから、数列は発散する。
【問題3】
1.
ab=bのbについての解は、f(b)-a=0のbについての解である。
問題1より、f(x)は1≦x≦eで単調増加である。
また、f(1)=1,f(e)=e1/eである。
従って、1≦a≦e1/eなるaに対して、1≦b≦eの解が1つだけ存在する。
2.
axはa≧1,x≧1の時、xについて単調増加である。
従って、b≧x≧1なるxに対して、
b=ab≧ax≧a1=a1である。
ここで、仮にan-1=x≦bで、an>bとなることがあったとすると、
an=ax>bとなり、先の不等式と矛盾する。
したがって、an>bとなることはない。
3.略
1≦x≦b(b=ab,1≦b≦e)でax≧xが示せるので、数列は常に増加する。
4.
数列が、極限値を持つとしたら極限値はβ=aβを満たすβである。
βのうち1≦β≦eを満たすβ=bは1つだけ存在し、
数列はan≧an-1≧1で
an>bとなることはないから、極限値bを持つ。
bは、b=abの1≦b≦eにおける解であるが、初等関数ではあらわせないと思われる。
特殊な例では、
a=1のときb=1,
a=![]() のときb=2,
のときb=2,
a=e1/eのときb=eとあらわせる。
【問題5】
問題4の誘導とは別の方法で証明してみる。
まず、命題1,2を証明する。
<命題1>
0<a<1のとき、x=axを満たすx=X1(a<X1<1)が1つだけ存在する。
<証明1>
f1(x)=ax、g(x)=xとおく。
f1(x)は単調減少関数、g(x)は単調増加関数である。
f1(0)=1,f(1)=a,g(0)=0,g(1)=1であるから、
f1(x)=g(x)を満たすx=X1(a<X1<1)が1つだけ存在する。
<命題2>
0<a<1/eeのとき、a^(ax)=xを満たす
x=X2 (X1<X2<aa)が存在する。
<証明2>
f2(x)=a^(ax)とおく。
f2の性質を調べるために、f2をxで微分する。
f2'(x)=f2(x) ax(log a)2 >0
これより、f2は単調増加であることがわかる。
さらにf2(0)=a,f2(1)=aa>aである。
f2(x)=g(x)の1つの解は、x=X1である。
x=X1における、f2の微分係数を求めると,
f2'(X1)=(X1 log a)2=(log X1)2となる。
ここで、X1<1/eすなわちa<1/eeを考えると、
f2'(X1)>g'(X1)=1 となる。
よって、X1の右近傍 X1+Δx (Δx→+0)では次式が成立する。
f2(X1+Δx)-g(X1+Δx)>0
さらにf2(1)-g(1)=aa-1<0である。
従って、a<1/eeのとき、
f2(x)=g(x)をみたすx=X2 (X1<X2<aa)が少なくとも1つ存在する。
<問題5の証明>
X2のうち最大のものをX2mとし、X2m<x≦1なるxを考える。
このとき、f2(x)-x<0が成立する。
また、a2=f2(1)=aa であるので、
a2n>X2mの範囲で、
a2n+2<a2nとなることがわかる。
さらに、f2は単調増加であるので、
X2m=f2(X2m)<f2(x)となり、a2n<X2mとならないことがわかる。
数列が収束するとすれば、極限値はX1(<X2m)であるが、
a2n≧X2mであるので、数列は収束しない。
a2nはX2mに収束するが、X1≠X2mであるので
a2n≠a2n+1となり、数列は振動する。
【問題6】
1〜3省略
4.以下の命題から証明する
<命題3>
1>a≧1/eeのとき、
a^(ax)=xを満たすxは、x=X1 唯一である。
<略証3>
f2'(x)=f2(x) ax(log a)2 ≦1が成立する。
f2(0),f2(1),g(0),g(1)の値とg'(x)=1、および以上の性質より、
X1以外の解が存在しないことが証明される。
<問題6証明 略証>
問題5のときと同様に、X1<x≦1なるxを考えると、
a2n+2<a2n、 a2n≧X1が証明できる。
X1はf1(x)=g(x)を満たすから、
a2n+1=a2nも成り立ち、数列が収束する。
収束値はX1である。
◆愛知県 Y.M.Ojisan さんからのコメント。
この問題はF(X)=0という非線形方程式を
X=F(X)−X(=aX)という形の反復式で数値計算する場合に現れる状況をほぼ網羅していて、結果を解析的に検証可能なので、数値計算の練習問題としてよいなと思いました。
この観点から見た場合、下図のように解答のヒントが得られます。
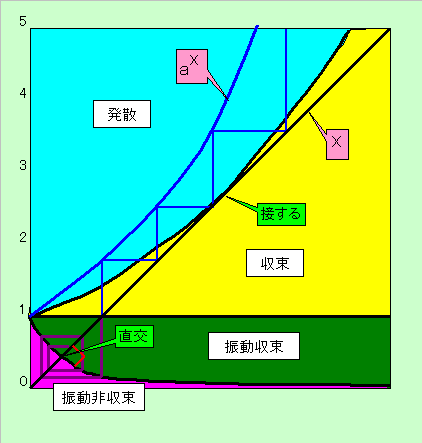
y=aXがy=Xと接する状態より上(空色領域)では、反復結果は図中の階段状の青線となり、
y=aXとy=Xの隙間をすり抜けて発散します。
一方それ以下でa>1の場合(黄色領域)は、
y=aXとy=Xが交差して上限を押さえ単調増加であるので、収束します。
収束しない場合としては2通りあり、安定振動の場合と発散振動の場合があります。
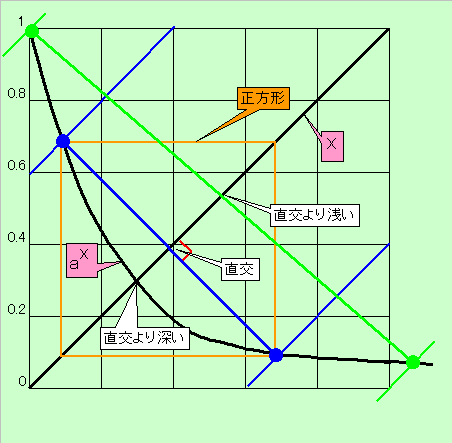
その判定は下図のように、y=Xから両側に等距離(青|緑)にある2直線と
y=aXとの交点を結ぶ直線の交差角が直角よりが浅いか深いかできまり、
aXの場合は緑の線の状態まで離れると必ず浅く交差することから、発散はせず2点間を振動することがわかります。
◆出題者のコメント。
>杉田さん
解答ありがとうございました。
まず,問題1および2については問題ないと思います。
一方,問題3の4,問題5の証明の最後の部分,問題6の4に共通して言えることですが,一般に,
「数列(xn)が収束するならば,極限値はxに限る」≠「数列(xn)が収束して,極限値はxである」に注意して,もう少し丁寧に証明する必要があると思います。
これらの点に注意して,もう一度検討していただければと思います。
>Y.M.Ojisan さん
丁寧に図解してくださりありがとうございました。
収束する場合としない場合で何が起こっているのかを大局的に把握することができました。