◆石川県 平田和弘 さんからの解答。
【問題1】
2辺をそれぞれx,y(y>x)とする。
y=x+a とおいて
xy=x(x+a)=(x+a/2)2−(a/2)2・・・(A)
となるので、上記に三平方の定理を適用する。
要するに、x+a/2 を斜辺とし、a/2を他の1辺とする直角三角形を考える。
このとき、直角三角形の外心は斜辺の中点にあることを利用する。
はじめ、二次方程式の解法穂の方法で考えていましたがうまくいきませんでした。
そこで、直角三角形の性質を利用してみました。
◆静岡県 ヨッシー さんからの解答。
【問題1】
<作図方法>
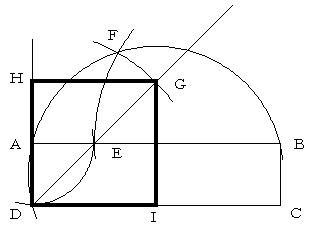
与えられた長方形をABCDとし、
a=AB、b=CD(ただしa>b)とする
1.中心A、半径ADの円と、ABの交点をEとする
BE=a−bとなる
2.長方形の外接円を描く(方法は省略)
![]() である
である
3.中心B、半径BEの円と、2.の円との交点をFとする
△BDFは∠F=90°の直角三角形であり、
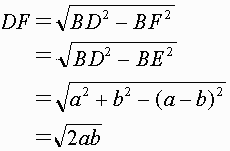
4.直線DEを引く
∠ADE=45° である
5.中心D、半径DFの円と、4.の直線との交点をGとする
6.点Gから、直線AD、直線DCに下ろした垂線(方法は省略)の足をH、Iとすると、四角形DHGIが求める正方形である。
対角線
![]() なので、
なので、
![]()
よって正方形DHGIの面積はabとなり、長方形ABCDの面積と等しくなる。
◆東京都 Asami さんからの解答。
【問題1】
与えられた長方形をABCDとします。
Aを中心にしてABの長さを半径とする円をコンパスで描くとAB,ADのどちらが長いかわかります。
もし両者が等しければ正方形そのものなので、ここではAB<ADとして考えることにします。
Aを中心にしてABの長さを半径とする円とADとの交点をEとして、EDを弦に含むような円Oを描きます。
あとはAから円Oへ接線を引けばAから接点までの長さが求める正方形の一辺の長さになります。
(方ベキの定理を考えればいいです。)
◆静岡県 ヨッシー さんからの解答。
【問題2】
まず、この作図の前提条件として、縦横比がある範囲内でないとうまく書けません。
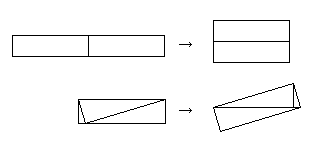
もし、不適当な比率の場合は、以下のようにあらかじめ変形した長方形を書いておき、作図後、元の位置に線を引き直せば、元の長方形の分割が出来ます。
また、作図の結果、分割された図形が四角形や五角形のまま残っていますが、対角線で三角形に分割できるので、問題ないと思われます。
ここでは、縦横比において、上記の条件を満たすものについて考えます。
また、目的の正方形の1辺の長さrは、問題1の方法ですでに得られているものとします。
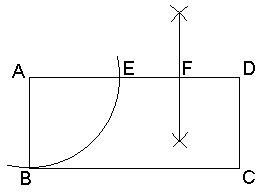
長方形ABCD(AB<BC)が与えられたとき、
辺AD上にAE=ABとなる点Eを取り、EDの中点をFとします。
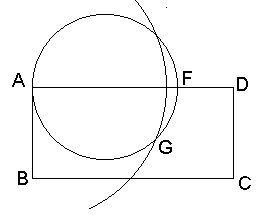
AFを直径とする円と、Aを中心とし半径rの円の長方形内での交点をGとします。
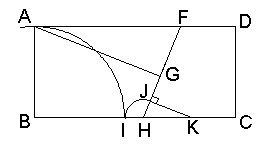
直線FGと辺BCの交点をHとします。
辺BC上にBI=ABとなる点Iを取り、
FH上にHI=HJとなる点Jを取ります。
点JからFHに垂直な直線とBCとの交点をKとします。
ここで分割された四角形ABHG、五角形CDFJK、三角形AGF、三角形HJKを組み替えると以下のような正方形AGLMが出来ます。
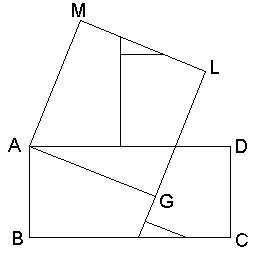
三角形HJKが裏返っていますが、これが許されないなら、HKの中点とJを結ぶ線で分割すれば、二等辺三角形が2つ出来ますので、裏返さずに組み替えることもできます。
◆静岡県 ヨッシー さんからの解答。
【問題2の解答の補足】
点E,Fを求めたあと、ED,AFを直径とする円を描けば、正方形の1辺の長さrを別途求めなくても、点Gが定められます。
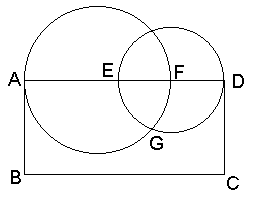
◆岩手県 utu さんからの解答。
(1) 辺の比が2倍未満のとき
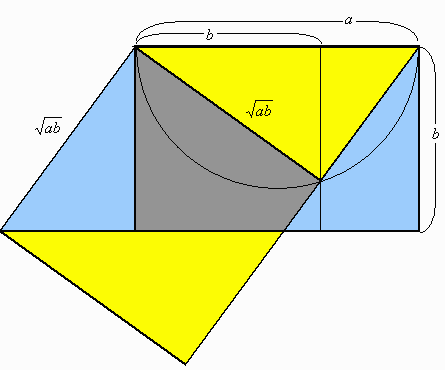
(2) 辺の比が2倍以上のとき
目的の正方形を斜めにずらして網の目に切っていく。
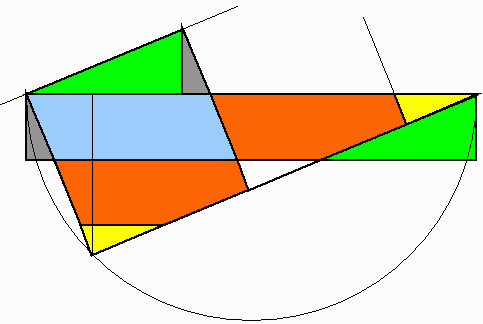
【おまけ】
六角形でも作れます。
いったん長方形にしてから正方形
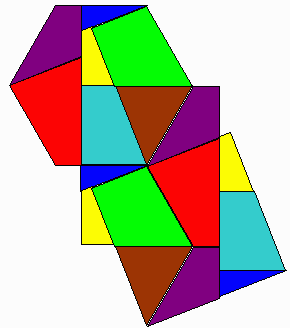
でも、よく見ると、黄色と水色、茶色と緑は、最終的にまたくっつくので、長方形を経由しないで、