◆山梨県 Footmark さんからの解答。
どのような凸四角形ABCDも、4頂点の内の3つを頂点とする三角形は4つある。
その4つの各三角形において、中点連結の定理より以下が言える。

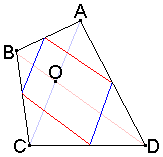
図の2本の青い線は共に、対角線ACと平行で長さはACの半分。
同様に、図の2本の赤い線は共に、対角線BDと平行で長さはBDの半分。
よって、どのような凸四角形ABCDにおいても、ABCD(1)は平行四辺形。
それ故、任意の正整数nに対して、ABCD(1)とABCD(2n+1)とは相似。
(辺比2n:1)
すると、ABCD(1)が正方形でなければ、何度同じ操作を繰り返しても永遠に正方形にはならない。
何故なら、1度正方形になると以後は永遠に正方形の筈である。
ABCD(1)が正方形となる条件は明らかに以下の2つ。
(1) 凸四角形ABCDの2本の対角線であるACとBDは、長さが等しい。
かつ
(2) 凸四角形ABCDの2本の対角線であるACとBDは、互いに直交する。
そこで、2本の対角線の交点をOとすると、(2)の条件より
AB2=AO2+BO2
BC2=BO2+CO2
CD2=CO2+DO2
DA2=DO2+AO2
よって、
AB2+CD2
=BC2+DA2
=AO2+BO2+CO2+DO2
[ P・S ]
(1)の条件は証明には必要ないので、[正方形]でなく[ひし形]や[長方形]で十分だったですね。
何故なら、任意の正整数nに対して、以下が言えます。
ABCD(1)が[ひし形]なら、ABCD(2nー1)同士は相似の[ひし形]で、ABCD(2n)同士は相似の[長方形]。
ABCD(1)が[長方形]なら、ABCD(2nー1)同士は相似の[長方形]で、ABCD(2n)同士は相似の[ひし形]。
◆宮城県 甘泉法師 さんからの解答。
正方形ABCD(N)の頂点の座標を(1,0)(0,1)(-1,0)(0,-1)として
四角形ABCD(N-1)の頂点の座標は
a,b>0、1<a+b<3 を使い
A(a,b)、B(-a,2-b)、C(a-2,b-2)、D(2-a,-b)
AC ⊥ BD すなわち対角線が直交する。
四角形ABCD(N-1)の対角線が直交するので
一般に頂点の座標は p,q,r>0 を使い
(1,0)、(0,p)、(-q,0)、(0,-r)
四角形ABCD(N-2)の頂点の座標は a,bを使い
A(a,b)、B(-a,2p-b)
C(a-2q,b-2p)= (-2+a,-2r+b)、D(2-a,-b)
これからq=1、r=p
すなわち四角形ABCD(N-1)はひし形で
四角形ABCD(N-2)の対角線は直交する。
こうして遡っていくと四角形ABCD(1)の対角線は直交する。
対角線が直交することと
AB2+CD2=BC2+DA2は同値。
対角線ADにB,Cから垂線を引いてピタゴラスの定理を使えば明らか。
(証明終)