仧峀搰導丂惔愳丂堢抝丂偝傫偐傜偺夝摎丅
亂栤戣侾亃
嶌愴
亂栤戣俀亃
偙偺嶌愴偑嵟慞偩偲偡傞偲偒丄徿嬥偺婜懸抣偼丄
俇亊乮侾乛俇乯亖俇乛俇
俆亊乮侾乛俇乯亖俆乛俇
丂丂俁俁乛侾俉
俇亊乮侾乛俇乯亊乮俀乛俁乯亖俇乛俋
俆亊乮侾乛俇乯亊乮俀乛俁乯亖俆乛俋
係亊乮侾乛俇乯亊乮俀乛俁乯亖係乛俋
丂丂俁侽乛侾俉
俇亊乮侾乛俇乯亊乮侾乛俁乯亖俇乛侾俉
俆亊乮侾乛俇乯亊乮侾乛俁乯亖俆乛侾俉
係亊乮侾乛俇乯亊乮侾乛俁乯亖係乛侾俉
俁亊乮侾乛俇乯亊乮侾乛俁乯亖俁乛侾俉
俀亊乮侾乛俇乯亊乮侾乛俁乯亖俀乛侾俉
侾亊乮侾乛俇乯亊乮侾乛俁乯亖侾乛侾俉
丂丂俀侾乛侾俉
丂俁俁乛侾俉亄俁侽乛侾俉亄俀侾乛侾俉
亖俉係乛侾俉
亖侾係乛俁
丂丂摎偊丂侾係乛俁枩墌丅
僾儘僌儔儉傪慻傫偱僔儈儏儗乕僔儑儞偟偨寢壥係侽侽侽侽夞偺幚尡偱係丏俇俇俆偲側傝傑偟偨丅
仧曗懌
丂侾夞偱偁傟偽丄婜懸抣偼俁丏俆枩墌丅
侾丆俀丆俁偺偲偒師偺僒僀僐儘傪怳傞嶌愴偺偲偒偺婜懸抣偼俁俈乛俉枩墌丅
侾係乛俁亅俁俈乛俉亖侾乛俀係丅
侾侽侽侽侽亊侾乛俀係亖係侾俇丏俇俇
栺係侾俇墌俇俇慘偺嵎偑偁傞丅
幚尡偱係丏俇俇俇傑偱妋掕偝偣傞偨傔偵偼俀侽侽枩夞埲忋偺帋傒偑昁梫偺傛偆偱偡丅
俀侽侽枩夞偺偲偒丄係丏俇俇俉俉俇偱偟偨丅
仧晲揷丂棽巌丂偝傫偐傜偺夝摎丅
堦夞僒僀僐儘傪怳偭偨偲偒丄偁傞悢偺弌傞妋棪傪倫偲偡傞偲丄
| 倫亖 | 侾 乗乗 俇 |
亙嘥亜値亖侾偺偲偒丄
俵(侾)亖倫亊(侾亄俀亄俁亄係亄俆亄俇)亖俁丏俆
亙嘦亜値亖俀偺偲偒丄
丂亙嘥亜偺寢壥傛傝堦夞栚偺弌栚偑丄俁埲壓偺応崌偼怳傝側偍偡偺偑椙偄丅
堦夞栚偵係,俆,俇偑弌傞妋棪偼丄偦傟偧傟倫偩偐傜丄
俵(俀)亖倫亊(係亄俆亄俇)亄俁倫亊俵(侾)亖係丏俀俆
亙嘨亜値亖俁偺偲偒丄
丂亙嘦亜偺寢壥傛傝堦夞栚偺弌栚偑丄係埲壓偺応崌偺傒怳傝側偍偡偺偑椙偄丅
堦夞栚偵俆,俇偑弌傞妋棪偼丄偦傟偧傟倫偩偐傜丄
俵(俁)=倫亊(俆亄俇)亄係倫亊俵(俀)亖係丏俇俇俇
亂僐儊儞僩亃
丂偍擇恖偺曽偐傜傎傏摨帪偵夝摎偑棃傑偟偨丅
庬杮偲寢壥偑堘偭偰嬃偒傑偟偨偑丄帺暘偱寁嶼偟偰傒傞偲偳偆傕杮偺曽偑娫堘偭偰偄傞傛偆偱偡丅
僔儈儏儗乕僔儑儞偺寢壥偲斾傋偰丄杮偺悢抣偑彫偝偄傛偆偱晄怰偵巚偭偰偄偨偺偱偡偑丄係丏俇俇俇丒丒丒偱惓偟偄偲妋怣偟傑偟偨丅
偱傕摉慠偐傕偟傟傑偣傫偑丄偩傫偩傫懨嫤偡傞儔僀儞偑壓偑偭偰偔傞偺偑柺敀偄偱偡偹丅
偍尒崌偄側偳偱傕摨偠偱偟傚偆偐丅
仧搶嫗搒丂朠丂墱恖丂偝傫偐傜偺夝摎丅
嵟弶偵峫偊偨偺偼丄
| 侾夞偩偗僒僀僐儘傪怳偭偰傗傔傞偙偲偑慜採偺応崌偺婜懸抣偼35000墌丅 偩偐傜丄偦傟傛傝懡偄徿嬥傪妉摼偱偒傞応崌乮亖係埲忋偑弌偨応崌乯偼偦偺応偱傗傔丄偝傕側偔偽師傪怳傞 |
偲偄偆傕偺偱偟偨丅偡側傢偪
乽侾夞栚傕俀夞栚傕丄係埲忋偑弌傟偽偦偙偱傗傔丄俁埲壓側傜傕偆侾夞怳傞乿丅
偝偰丄専徹偵擖偭偰傒傑偟傚偆丅
侾夞栚偼倎埲忋偑弌偨傜傗傔丄俀夞栚偼倐埲忋偑弌偨傜傗傔傞傕偺偲偟傑偡偲丄婜懸抣偼
| 10000a亊 | 1 6 |
亄10000(a+1)亊 | 1 6 |
亄丒丒丒亄60000亊 | 1 6 |
| 亄 | a-1 6 |
亊(10000b亊 | 1 6 |
亄10000(b+1)亊 | 1 6 |
亄丒丒丒亄60000亊 | 1 6 | ) |
| 亄 | a-1 6 |
亊 | b-1 6 |
亊(10000亊 | 1 6 |
亄20000亊 | 1 6 | 亄丒丒丒亄60000亊 | 1 6 | ) |
侾峴栚偼侾夞栚偱傗傔傞応崌
俀峴栚偼俀夞栚偱傗傔傞応崌
俁峴栚偼俁夞栚傑偱怳傞応崌丂丒丒丒偱偡丅
偙傟傪寁嶼偟偰丄嵟戝抣傪弌偡倎偲倐偺慻傒崌傢偣傪媮傔傞偙偲偵側傝傑偡偑巹偵偼偪傚偭偲擄偟偄偺偱丄Excel偺彆偗傪庁傝偰傗傝傑偡丅
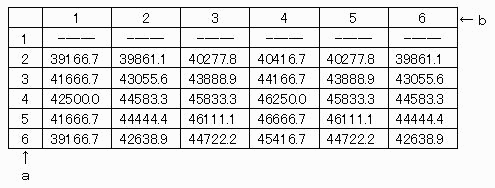
偡傞偲丄壓昞 偺傛偆偵側傝傑偡丅
乮彫悢揰埲壓戞俀埵偱巐幪屲擖乯

仸倎亖侾丄偮傑傝乽侾夞栚偱侾埲忋偑弌偨傜偦偙偱傗傔傞乿偲偼乽侾夞栚偱壗偑弌傛偆偲俀夞栚偼怳傜側偄乿偲偄偆偙偲側偺偱丄偙偺昞偐傜偼彍奜偟傑偟偨丅
偪側傒偵丄偙偺応崌偺婜懸抣偑35000墌偱偁傞偙偲偼偡偖媮傔傜傟傞偼偢偱偡丅
堄奜傗堄奜丄乽侾夞栚偱俆埲忋偑弌偨傜偦偙偱傗傔丄俀夞栚偼係埲忋側傜偦偙偱傗傔傞乿偺偑堦斣婜懸抣偑崅偄傛偆偱偡丅
偝偭偦偔幚尡偟偰傒傑偟偨偲偙傠丄侾侽侽夞傗偭偰暯嬒妉摼徿嬥偼栺47,180墌偱偟偨丅
偄偄姶偠偱偡丅