『タイルと針』解答

◆岡山県　藤井　さんからの解答。

【問題２】

平面全体で考えるとやっかいなので、a×a の１つのタイル内で考えます。

針の中心をこのタイル内にとり、その時タイルの周りと交わる角度が取り得る範囲を考えます。
（１つのタイル内で考えるかわりに、円環面内で考えても同じ（だと思う）で、この場合扱う全体は 円環面の３次元版になります（円周×円周×円周）。）

扱う全体の大きさは 2πa²。

タイルを次の３つの部分に分けます。(a ≧ l)

(1) どの辺からの距離も l/2 を越える部分。

(2) 各頂点からの距離が l/2 以内の部分。

(3) ある１辺からの距離は l/2 以内だが、他の辺からの距離はl/2 を越える部分。

(4) 各頂点からの距離が l/2 を越え、ある２辺からの距離が l/2 以内の部分。

(1) の場合、どの角度でも交わることがない。
(2) の場合、どの角度でも常に交わる。
(3) の場合、１つの辺と交わる。
(4) の場合、２つの辺と交わる。ただし、同時に２つの辺とは交わらない。

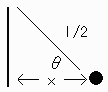
このことから、(1), (2)の場合はすぐに求まる。
(1) 0
(2) 半径 l/2 の円の面積 × 2π = (πl)² / 2

(3) の場合を考える。

交わる辺からの距離を x として、
2x/l = cos θ と置けば、交わる角度の範囲は
合計 4θ= 4 Arccos 2x/l あることがわかる。
（この図だと、上、下、それぞれの向きを１８０度かえたもの）

また、(3) の１つ分は、

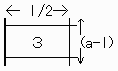
となっていて、４個所あるので。

4(a-l)

l/2 ∫ 0

4 Arccos 2x/l dx

=16(a-l)* l/2

∫ θ sin θ dθ

= 8(a-l)l

(4) の場合は、１つ分が、

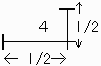
となっており、交わる１辺からの距離を x とすれば、そこでの幅は、

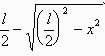
である。
（l/2 から 半径 l/2 の円の部分を除くため）

４個所、２辺について求めるため、

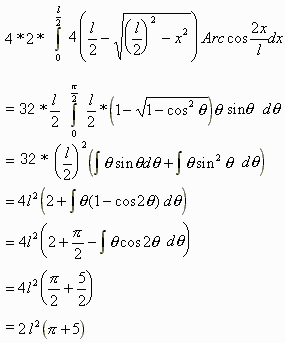
これらから、針がタイルの周と交わる確率 p は、

p = (8(a-l)l +2 l²(π + 5) + (πl)² / 2)/(2πa²)
　= l((π²/2 + 2π + 2)l + 8a)/(2πa²)
　= (l/a)²(π/4 + 1 + 1/π) + 4(l/a)/π

となる。

立方体で考えるとどうなるのだろうか？

◆愛知県　juin　さんからの解答。

【問題２】

正方形の１辺の長さa,針の長さ１。
まず、間隔aで引かれた直線と針が交わる確率を求める（ビュフォンの針）

針の中心x,針が水平線となす角θとし、[0,a)×[0,π)で考える。

交わる時は、x＜

1 2

sinθまたは、a-x＜

1 2

sinθだから、

∫

1 2

sinθ dθ+∫

1 2

sinθ dθ=1+1=2

よって確率は

2 aπ

タイルの場合　Ω=[0,a)×[0,a)×[0,π)とし、体積に比例した確率Pを入れる。

A={水平線と交わる},B={垂直線と交わる}とする。
P(A∪B)を求める。
P(A∪B)=P(A)+P(B)-P(A∩B)

P(A)=P(B)=

2 aπ

だから、P(A∩B)を求める。

正方形の四隅で同じことがおこるので、(0,0)の近くで考える。
この集合をCとする。
C={(x,y,θ)∈A∩B|(0,0)の近くで２辺と交わる}　

θを１つ固定する、つまり、条件付き確率を考える。

●

π 2

＜θ＜π

のとき、

P(C|θ)

=P(x＜-

1 2

cosθ,y＜

1 2

sinθ|θ)

=P(x＜-

1 2

cosθ|θ)･P(y＜

1 2

sinθ|θ)

=-

1 2a

cosθ

×

1 2a

sinθ

=	cosθsinθ -4a2

θで[

π 2

,π)の範囲で積分して、

∫P(C|θ)P(dθ)=∫

cosθsinθ -4a2

dθ=

1 8a2

● 0＜θ＜

π 2

のとき、

針の重心を含むタイルの外でも交点ができます。

P(C|θ)

=P(x＜

1 2

cosθ,y＜

1 2

sinθ|θ)

=P(x＜

1 2

cosθ|θ)･P(y＜

1 2

sinθ|θ)

=

1 2a

cosθ

×

1 2a

sinθ

=	cosθsinθ 4a2

θで[0,

π 2

)の範囲で積分して、

1 8a2

となる。

よって、[

π 2

,π)の場合と合計して、P(C)=

1 4a2

P(A∩B)=4×

1 4a2

=

1 a2

よって、

P(A∪B)=

2 aπ

+

2 aπ

-

1 a2

=

4 aπ

-

1 a2

となる。

◆愛知県　juin　さんからの解答。

【問題３】

正６角形の頂点を反時計周りにA,B,C,D,E,Fとする。
時計の数字と対応させると、１１時、９時７時、５時、３時、１時となる。
Cを原点とし、CDをx軸に重ねる。
CAをy軸に重ねる。

k1={CDと平行な直線と針が交わる},
k2={BCと平行な直線と交わる},
k3={ABと平行な直線と交わる}とする。

P(k1∪k2∪k3)を求める。

P(k1)=

4 aπ3

となる。

理由。

CD,FA,対角線BEなど、

間隔

a 2

で引かれた直線と針が交わる確率は

ビュフォンの針の問題と同じだから、

2 aπ 2

=

4 aπ

辺の部分と対角線の部分の比は、1:2だから３で割り、

P(k1)=

4 aπ3

P(k1∪k2∪k3)
=P(k1)+P(k2)+P(k3)-P(k1∩k2)-P(k2∩k3)-P(k3∩k1)+P(k1∩k2∩k3)

P(k1∩k2∩k3)=0だから、P(k1∩k2)を求める。

正６角形の内部に針の中心が落ち、針とx軸とが作る角を考え、直積空間に直積確率をいれる。

正６角形の面積は

3a2 2

、

角度は0≦θ＜πだから、長さπ。

Cの近くで２辺と交わる場合を計算する。

0≦θ＜

π 3

のとき。

θを１つ固定して条件付き確率を考える。

P(Cの近くで２辺と交わる|θ）＝(

cosθ 2

-

sinθcosθ

)

sinθ 4

となる。

[0,

π 3

)の範囲で、θで積分すると

1 64

となる。

[

π 3

,

2π 3

)の場合も同じで

1 64

。

[

2π 3

,π)の場合、条件付き確率は

1 2

4sinθsin(θ-

2π 3

)・

6

となり、

[

2π 3

,π)の範囲でθで積分して

1 4

-

π 12

合計

1 64

+

1 64

+

1 4

-

π 12

=

9 32

-

π 12

６つの頂点で同じ値だから
P(k1∩k2)+P(k2∩k3)+P(k3∩k1)

=6(

9 32

-

π 12

)／(

3a2 2

π)

=

9 8a2π

-

1 9a2

求める確率は
P(k1∪k2∪k3)

=

3×4 aπ3

-

9 8a2π

+

1 9a2

=

4 aπ

-

9 8a2π

+

1 9a2

となる。

　『タイルと針』へ

　数学の部屋へもどる