◆千葉県 なのはな さんからの解答。
【問題1】
52X431=22412
【問題2】
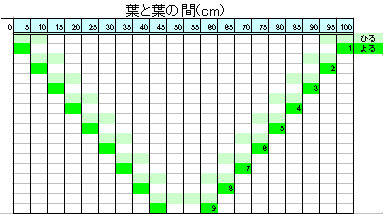
9日めの昼間に、葉と葉の間はなくなります。

【問題3】
商人
…全体の「4分の1」
…残りは全体の「4分の3」
1人目の弟子
…全体の「4分の3」の「3分の1」
すなわち、全体の「4分の1」
…残りは全体の「4分の2」
2人目の弟子
…全体の「4分の2」の「2分の1」
すなわち、全体の「4分の1」
…残りは全体の「4分の1」
3人目の弟子
…残り全部
すなわち、全体の「4分の1」=12個
商人と3人の弟子はそれぞれ、12個ずつもらった。
最初にアメは全部で48個あった。
【問題5】
チョコが20個、ガムが1個、ラムネが6個、飴が30個。
1/60をもとにして考えればわかります。
1/3は20/60、1/10は6/60、1/2は30/60です。
1/60+20/60+6/60+30/60=57/60
駄菓子1個とカステラ2個を加えるとちょうど60個になります。
◆広島県 清川 育男 さんからの解答。
【問題4】
3位にならなければよいから、
30÷3=10
10+1=11
11票取れば必ず2位以上になれる。
◆山梨県 Footmark さんからの解答。
【問題4】
はじめに一般解を示します。
(落選者数ー1)人の挙手の数の合計が最少の時、
(当選者数+1)人の挙手の数の合計は最大になります。
その最大の挙手の数の合計を(当選者数+1)人で可能な限り均等に分配しても、(当選者数)番目以上の挙手の数があれば確実に当選できます。
元の問題に戻ります。
各立候補者は立候補するくらいだから当然自分自身に手を挙げるものとします。
1人(落選人数ー1人)の挙手の数が最少の時は、自分だけの1です。
最少を1にして残りを3人(当選人数+1人)で可能な限り均等に分配すれば、合計30の挙手の数は以下になります。
30=10+10+9+1
ですから、最低10人が手を挙げれば確実に学級委員になれます。
ちなみに、立候補者が自分以外に手を挙げることも許されるものとすると、
30=10+10+10+0
なので、10人では確実に学級委員になれるとは限りません。
[PS]
とても面白い問題ですね。
興味があったので先に一般解を求めてみました。
◆東京都 葛衣 奥人 さんからの解答。
【問題2】
2つの葉の間隔は昼は20cm短く、夜は10cm長くなるという意味ですね?
つまり1日で10cm短くなる。
8日経過した時点で80cm間隔が詰まり、残り20cm。
9日目の昼間でこの20cmの間隔がゼロになります。
よって答えは9日
【問題3】
| 商人がとった分は | 1 4 | 、残り | 3 4 |
| 一人目の弟子がとった分は | 3 4 | × | 1 3 |
、残り | 2 4 |
| 二人目の弟子がとった分は | 2 4 | × | 1 2 |
= | 1 4 |
、残り | 1 4 |
というわけで、
| 三人目の弟子がとった分は | 1 4 | で、これが12個。 |
| ・・・なんだ。全員 | 1 4 | ずつじゃないか! |
というわけで、
【問題3-1】
全員12個ずつ
【問題3-2】
最初のアメは48個
【問題4】
11人。
あなたがAさんで、他の3人がB・C・Dさんとします。
手を上げた人数を投票数ということにします。
得票数はB≧C≧Dということにします。
Aさんが10票のとき
B=10、C=10、D=0 だと、3人同数なので決定しない。
Aさんが11票のとき
B=10 だとDさんがゼロでもCさんは9票。1位のAさんと2位のBさんで確定。
B=11 だと、同様に考えてAさんとBさんが同点1位で確定。(C≧8)
B≧12 だと、1位のBさんと2位のAさんで確定。(C≧7)
※B≦9だと、CさんかDさんが10票以上獲得していることになるのでここでは考えません
ということで、ここが境目です。
ひょっとして、n人を選ぶとき、全体の(n+1)分の1より多ければいいのでしょうか?
【問題5】
チョコ+ガム+ラムネ+飴
| = | 1 3 | + | 1 60 | + | 1 10 | + | 1 2 |
| = | 57 60 |
| 残り | 3 60 | が駄菓子+カステラ=3個、 |
というわけで、
チョコ=20個、ガム=1個、ラムネ=6個、飴=30個
【問題6】
算数で、ってところがキビシイですね・・・
エスカレーターの距離を60とすると、歩いた場合の上りの速度は秒速3、下りの速度は秒速1。
で、エスカレーターの速度をエ速、歩く速さを歩速とすると
歩速+エ速=3
歩速-エ速=1(エ速の方が速かったら下れない!)
ということですね。
--1--------歩速--------3--- |--エ速---||---エ速--|上の図から、エ速=1であることがわかります。(苦しいなぁ)
よって、歩かずに上につくまでにかかる時間は
60÷1=60(秒)です。
◆三重県の小学生 CHIHIRO さんからの解答。
【問題2】
9日目の昼に2つの葉の間はなくなる。
1日目 20㎝近ずき10㎝はなれる(今まで近づいたきょり…10㎝) 2日目 〃 (今まで近づいたきょり…20㎝) 3日目 〃 (今まで近づいたきょり…30cm) 4日目 〃 (今まで近づいたきょり…40㎝) 5日目 〃 (今まで近づいたきょり…50㎝) 6日目 〃 (今まで近づいたきょり…60㎝) 7日目 〃 (今まで近づいたきょり…70cm) 8日目 〃 (今まで近づいたきょり…80㎝) 9日目 20㎝近づいて間はなくなる(今まで近づいたきょり…100cm《1m》)…というわけです。
≪感想≫
以前、この問題と似たようなかんじの問題をやったことがあったので、これも一応解いてみました。
数学は苦手ですが…この手の問題は、簡単で楽しいですね!!('。')
◆和歌山県の中学校3年生 大岩 真知子 さんからの解答。
【問題5】
チョコレ-ト20個
ガム1個
ラムネ6個
あめ30個
おもしろかったです。
◆千葉県 なのはな子 さんからの解答。
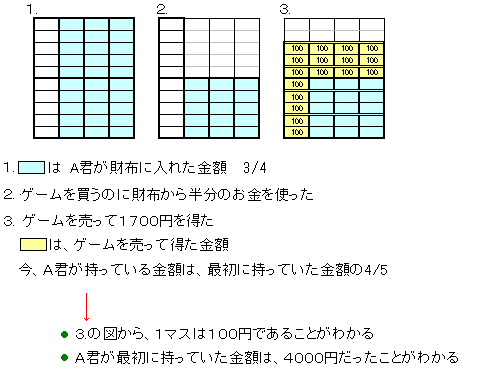
【問題7】
| A君が持っている全額・・・X |
| 財布に入れた金額・・・・・ | 3 4 | X |
| 買ったゲームの代金・・・・・ | 3 4 | X× | 1 2 | = | 3 8 | X |
| 財布に残った金額・・・・・ | 3 4 | X× | 1 2 | = | 3 8 | X |
| ゲームを売って得た金額・・1700 |
| 今、持っている金額・・・・ | 3 8 | X+1700 |
| (=最初に持っていた金額の | 4 5 | ) |
| 4 5 | X= | 3 8 | X+1700 |
| 4 5 | X- | 3 8 | X=1700 |
| 32 40 | X- | 15 40 | X=1700 |
| 17 40 | X=1700 |
| X=1700× | 40 17 | =4000 |
【問題7別解】
これなら小学生にも納得してもらえるでしょうか…?
◆千葉県 なのはな子 さんからの解答。
【問題8-1】
| 8 16 | + | 4 16 | + | 2 16 | + | 1 16 | = | 15 16 | …みつけたかけら |
| 残っているかけら… | 1 16 |
【問題8-2】
先にみつけたかけらと、さらにみつけたかけらを合わせる。
| 30720+1024+512+256+128+64+32+16+8+4+2+1
32768 | = | 32767 32768 | …みつけたかけら |
| 残っているかけらは全体の | 1 32768 |
【コメント】
この問題は計算しなくとも、最後のかけらを見ればわかるので面白いですね。
◆神奈川県の小学生 イヌネコ さんからの解答。
【問題8-1】
全体を16とすると、
| 16× | 1 16 | = | 1 |
| 16× | 1 8 | = | 2 |
| 16× | 1 4 | = | 4 |
| 16× | 1 2 | = | 8 |
したがって、16-(1+2+4+8)=1
| 答えは、 | 1 16 |
別解
| 1 2 | + | 1 4 | + | 1 8 | + | 1 16 | = | 15 16 |
| 1- | 15 16 | = | 1 16 |
【問題8-2】
| 1 32 | + | 1 64 | + | 1 128 | + | 1 256 | + | 1 512 | + | 1 1024 | + | 1 2048 | + | 1 4096 | + | 1 8192 | + | 1 16384 | + | 1 32768 |
| = | 2047 32768 |
| 15 16 | - | 2047 32768 | = | 1 32768 |
| 答えは、 | 1 32768 |
問題8-2は8-1の別解のほうでやりました。
◆島根県の中学校3年生 支離滅裂 さんからの解答。
【問題9】
全体で何人の人が賛成し、反対したかを見ます。
賛成は40人,反対は50人です。
a+2b+3c=40
2a+b+3d=50
どれか一つの意見に賛成した人はaになります。
2aと言うのは、どれか一つに賛成したなら、どれか二つに反対したと言う事なのでそうなります。
三つの意見に賛成した人はcとなります。
3cと言うのは、三つに賛成したと言う事で、合計を見るので3倍します。
これをa+2b+3c=40の式に代入して、15+2b+3=40を解いてb=11になります。
bと言うのは、式を見ても分かると思いますがどれか二つに賛成したという事です。
dは全てに反対した人です。
何故3倍かは、cの所と一緒です。
2a+b+3d=50に今やったことを代入して、
30+11+3d=50を解いてd=3です。
∴全てに反対する人(どの意見にも賛成しない人)は3人です。
【問題10】
○回目で何が出たかは分からないとして考えます。
そうすると、全体で7776通りの出方がある訳です。
| B君の出る確率は、 | 1 7776 | です。 |
| しかし、A君の出る確率は | 2 7776 | 以上になります。 |
∴A君の出る確率が多い
【問題10の別の解釈】
○回目で何が出たかを定めた場合、
| A君・B君とも確率は | 1 7776 | です。 |
∴A・B君とも出る確率は同じ
◆千葉県 なのはな子 さんからの解答。
【問題9】
☆どの意見にも賛成しなかったのは、3人
◆東京都 鳳 奥人 さんからの解答。
【問題7】
1700円を足した額、というのは、「ゲームを買ってその代金を支払った後の財布の残高に足した額」でしょうか?
| 全額× | 3 4 | =財布 |
| 買ったゲーム=財布× | 1 2 | だから |
| 財布に残った額も財布× | 1 2 |
| つまり(全額× | 3 4 | )× | 1 2 | =全額× | 3 8 |
| これに1700円を足したら全額× | 4 5 |
ということは、1700円というのは、
| 4 5 | - | 3 8 | = | 32 40 | - | 15 40 | = | 17 40 | だから |
| 全額の | 17 40 | にあたるということになります。 |
| ということで全額は1700÷ | 17 40 | =4000(円) |
【問題8】
なんだか、高校数学の「Σ」の問題を出されてるみたいでいやーな気分です(笑)
分母が2、2×2、2×2×2、2×2×2×2・・・であることがポイントですね。
| まず全体の | 1 2 | が見つかった→残りは1- | 1 2 | = | 1 2 |
| 次に全体の | 1 4 | が見つかった→残りは | 1 2 | - | 1 4 |
= | 1 4 |
| 次に全体の | 1 8 | が見つかった→残りは | 1 4 | - | 1 8 |
= | 1 8 |
| 次に全体の | 1 16 | が見つかった→残りは | 1 8 | - | 1 16 |
= | 1 16 |
・
・
・
| 次に全体の | 1 ○ | が見つかった→残りは | 1 ○ | ・・・なんだそういうことか! |
というわけで
| 問題8-1の答えは「 | 1 16 | 」、 |
| 問題8-2の答えは「 | 1 32768 | 」です。 |
【問題9】
クラスの人数は30人なのは明らかですね。
人数でなく、賛成の票数で数えると、賛成票数の合計は40です。
で、どれかひとつだけに賛成した人が15人
→この人たちが入れた賛成票も15票
3つの意見に賛成した人が1人
→この人が入れた賛成票は3票
残り22票が「どれか2つに賛成した人」の分ですが、この人たちは一人2票入れていることになるので、
人数は11人。
15+1+11=27
残る3人が「どの意見にも賛成しなかった人」です。
念のため、反対票数(合計50)で数えてみましょう。
3つの意見に反対した人 3人 票数:9
1つの意見に賛成した人(2つの意見に反対した人)15人 票数:30
2つの意見に賛成した人(1つの意見に反対した人)11人 票数:11
3つの意見に賛成した人(どれにも反対しなかった人)1人 票数:0
票数合計:50 ・・・ということで、これで正しいですね。
【問題10】
これは、たとえばA君については「1回目が1、2回目が6、3回目が3、・・・」になる確率、ということですか?
もしそうであれば、どの目についても出る確率は等しく1/6だから、同じだと思うのですが。。
◆東京都 tokujq さんからの解答。
【問題9】
クラスの人数は30人
投票の集計結果は 賛成票40 反対票50
そのうち30
1人は 3 0
15人は 15 30
のこりは14人が二つ賛成と全部反対だから
差し引き 賛成票22 反対票20 より
11人が二つ賛成 22 11
3人が全部反対 0 9
となる。
◆福岡県 micky さんからの解答。
【問題9】
ベン図が描けると良いのですが。
劇、演奏、クイズの順にA,B,Cとします。
賛成は、A20人,B10人,C10人です。
全部足すと、40人。
この中には、三つとも賛成の人(1人)が、3回入っています。
40-3=37
一つだけ賛成の人は、15人(この人たちは、1回しか入っていません)なので、
37-15=22
(2つに賛成の人で2回入っています)
22÷2=11
全部で、30人いますから、
30-(15+11+1)=3
答えは3人
【問題10】
AもBも
| 1 6 | × | 1 6 | × | 1 6 | × | 1 6 | × | 1 6 | = | 1 7776 |
◆東京都の中学校3年生 もやし さんからの解答。
【問題10】
Aさんの出た目の順番を考える場合 → どちらも同じ確率。
Aさんの出た目の順番を考えない場合
→ 積の法則から、Aさんの確率の分子は、
5×4×3×2×1=120通り ※
Bさんの確率の分子は無論1通り
二人とも分母は同じなので、Aさんのほうが高い。
※の理由
1回目 → 1・6・3・2・5のどれかがでればいいから5通り
2回目 → 1・6・3・2・5のうち1回目に出た目以外が出ればいいから4通り
3回目 → 1・6・3・2・5のうち2回目までに出た目以外が出ればいいから3通り
4回目 → 1・6・3・2・5のうち3回目までに出た目以外が出ればいいから2通り
5回目 → 1・6・3・2・5のうち4回目までに出た目以外が出ればいいから1通り
以上から、分子は5×4×3×2×1=120通り