 )
) 俁
 噋3
噋3仧嶳棞導丂Footmark 偝傫偐傜偺夝摎丅
仮俙俷俠偲仮俙俛俠偲仮俙俢俠偼俁曈偑摍偟偄偺偱崌摨偱偡丅
仮俛俷俢偲仮俛俙俢偲仮俛俠俢傕俁曈偑摍偟偄偺偱崌摨偱偡丅
傛偭偰丄仮俙俷俠偲仮俛俷俢偼崌摨偱丄捈妏俀摍曈嶰妏宍偱偡丅
偟偐傕丄偙偺俀偮偺嶰妏宍偼偳偪傜傕掙柺偵悅捈偱偡丅
偝傜偵丄偙偺俀偮偺嶰妏宍摨巑偼偍屳偄偵捈岎偟偰偄傑偡丅
惓巐妏悕俷-俙俛俠俢偺懱愊偼柧傜偐偵
(俇*俇)(俁 ) ) 俁 |
噋3亖俁俇 噋3 噋3 |
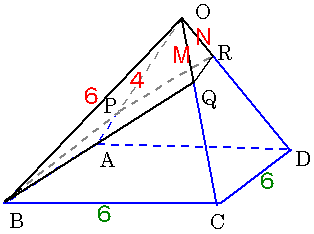
揰俹偲揰俛偼梌偊傜傟偰偄傞偺偱丄揰俻偺埵抲偝偊寛傑傟偽揰俼偺埵抲傕堦堄偵寛傑傝傑偡丅
乮壗屘側傜丄捈慄忋偵側偄俁揰傪娷傓暯柺偼侾偮偟偐側偄乯
慄暘俷俻偺挿偝傪 俵噋 偲偟丄偦偺帪偺慄暘俷俼偺挿偝傪 俶噋 偲偟傑偡丅
乮偨偩偟丄侽亙俵亝俇乯
傑偨丄柧傜偐偵慄暘俷俹偺挿偝偼 係噋 偱偡丅
巐妏悕俷-俹俛俻俼偺懱愊倁偼丄仮俙俷俠偺柺偱愗抐偟偰丄
| 掙柺愊偑 | 係俵 俀 |
偺俀偮偺嶰妏悕傪崌傢偣偨傕偺偲峫偊傞偲丄 |
| 偦傟偧傟偺崅偝偼丄 | 俇 |
偲 | 俶 |
偱偡丅 |
| 亪丂倁亖 | 俀俵(俶亄俇) 俁  |
仮俛俷俢偺柺偱愗抐偟偰丄
| 掙柺愊偑 | 俇俶 俀 |
偺俀偮偺嶰妏悕傪崌傢偣偨傕偺偲峫偊傞偲丄 |
| 偦傟偧傟偺崅偝偼丄 | 係 |
偲 | 俵 |
偱偡丅 |
| 亪丂倁亖 | (俵亄係)俶 |
| 亪丂 | 俀俵(俶亄俇) 俁  | 亖 | (俵亄係)俶 |
| 亪丂俶亖 | 侾俀俵 俵亄侾俀 |
偦偙偱丄巐妏悕俷-俹俛俻俼偺懱愊倁傪 俵 偩偗偱昞偡偲
| 倁亖 | 侾俀俵(俵亄係)  (俵亄侾俀) (俵亄侾俀) |
亂栤戣侾亃
柧傜偐偵 俵亖俀 側偺偱丄偙傟傪倁偺幃偵戙擖偡傞偲
| 倁亖 | 俁俇 俈 |
亂摎偊亃
俁俇 俈 | 噋3 |
亂栤戣俀亃
惓巐妏悕俷-俙俛俠俢偺懱愊偺敿暘偼丄侾俉 偱偡偐傜丄
偱偡偐傜丄
侾俀俵(俵亄係)  (俵亄侾俀) (俵亄侾俀) | 亖侾俉 |
亪丂俵2亄俵亅俁俇亖侽
偙傟傪夝偔偲丄![]()
偲偙傠偑 俵亜侽 側偺偱丄![]()
亂摎偊亃
![]() 噋
噋
{俹丒俽}
拞妛惗偺婔壗偱偼柤栤戣偩偲巚偄傑偡丅
仧弌戣幰偺僐儊儞僩丅
惓夝偱偡丅
偙偺傛偆側夝朄傪懸偭偰偄傑偟偨丅
偙傟偩偲拞妛惗偱傕夝摎偱偒傞庤朄偱偡偹丅
杮栤戣偼俹丆俻偑拞揰偺帪丄俼偺埵抲傪媮傔傞栤戣偺夵椙偱偟偨丅
掙柺偺拞怱傪俽偲偡傞帪丄俷俽丆俛俼丆俹俻偼堦揰偱岎傢傝傑偡丅
偙傟傪梡偄偰俼偺埵抲傪掕傔偰丄懱愊傪媮傔傞偲偄偆偺偑巹偑帩偭偰偄傞夝摎偱偟偨丅
偦偺夝摎偵斾傋偰丄Footmark偝傫偺夝摎偼幚偵娙寜偱傛偄偲巚偄傑偡丅