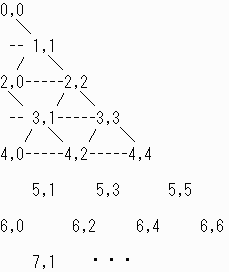
◆宮城県 甘泉法師 さんからのコメント。
より簡単な1次元の場合
数直線上 x、ステップs での存在確率 P(s;x)
最初原点に存在する。P(0;0)=1。
他のsとxでは P(s;x)=0。
次のステップで左右で半々の確率で1移動。
| P(s+1;x)= | 1 2 |
*P(s;x-1)+ | 1 2 |
*P(s;x+1) |
この関係式からえられたステップ5までのP(s;x)を表にあらわす。
| x\s | 0 | 1 | 2 | 3 | 4 | 5 |
| 0 | 1 | 0 | 1/2 | 0 | 3/8 | 0 |
| 1 | 0 | 1/2 | 0 | 3/8 | 0 | 5/16 |
| 2 | 0 | 0 | 1/4 | 0 | 1/4 | 0 |
| 3 | 0 | 0 | 0 | 1/8 | 0 | 5/32 |
| 4 | 0 | 0 | 0 | 0 | 1/16 | 0 |
| 5 | 0 | 0 | 0 | 0 | 0 | 1/32 |
対称なのでマイナスのxについては省略。
次に捕まえるトラップを考える
T(x)=0 xにトラップがある場合
T(x)=1 xにトラップがない場合
P(s+1;x)
| = | 1 2 |
*P(s;x-1)*T(x-1)+ | 1 2 |
*P(s;x+1)*T(x+1)+P(s;x)*(1-T(x)) |
最後の項はトラップにつかまったままであることを表す。
たとえばx=-3,3にトラップがある場合のP(s;x)の表は
| x\s | 0 | 1 | 2 | 3 | 4 | 5 |
| 0 | 1 | 0 | 1/2 | 0 | 3/8 | 0 |
| 1 | 0 | 1/2 | 0 | 3/8 | 0 | 9/32 |
| 2 | 0 | 0 | 1/4 | 0 | 3/16 | 0 |
| 3 | 0 | 0 | 0 | 1/8 | 1/8 | 7/32 |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 |
【コメント】
2次元格子の場合に拡張するのは
P(s+1;x,y)
| = | 1 4 |
*P(s;x-1,y)+ | 1 4 |
*P(s;x+1,y)+ | 1 4 |
*P(s;x,y-1)+ | 1 4 |
*P(s;x,y+1) |
とすればいいので簡単ですが、六角形の場合点の名まえのつけかたにてこずっています。
◆宮城県 甘泉法師 さんからの解答。
| 原点を中心に | 1 12 |
の中心角できったピースについて次のように点に番号をつける。 |
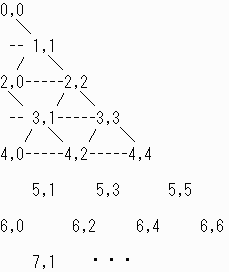
ステップs後の点(m,n)の存在確率をP(s;m,n)とあらわす。
P(s;m,n) = 0 n<0 または m>n または mとnの偶奇がことなる場合
P(0;m,n) = 1 (m,n)=(0,0)の場合
= 0 その他のm、n
P(s+1;m,n)
| = | 1 6 |
*P(s;m-1,n-1)*G(m,n;m-1,n-1)+ | 1 6 |
*P(s;m-1,n+1)*G(m,n;m-1,n+1)+ | 1 6 |
*P(s;m,n-2)*G(m,n;m,n-2)+ | 1 6 |
*P(s;m,n+2)*G(m,n;m,n+2)+ | 1 6 |
*P(s;m+1,n-1)*G(m,n;m+1,n-1)+ | 1 6 |
*P(s;m+1,n+1)*G(m,n;m+1,n+1) |
ここでGとFは図形の対称性を使い他のピースからの寄与をいれた係数で
G(i,j;k,l)=6、 (i,j)=(0,0)
G(i,j;k,l)=2、(i,j)が(0,0)を除く境界線上にあり、(k,l)が同じ境界線上にない
G(i,j;k,l)=1、その他の場合
F(m,n) = 2、(m,n)=(1,1)
F(m,n) = 1、m≠1かつn=1
F(m,n) = 0、その他の場合
さらにそこに行けばつかまる罠(トラップ)をおくことを考え,上の漸化式の各項に係数をかける。
P(s+1;m,n)
| = | 1 6 |
*P(s;m-1,n-1)*G(m,n;m-1,n-1)*T(m-1,n-1) + | 1 6 |
*P(s;m-1,n+1)*G(m,n;m-1,n+1)*T(m-1,n+1)+ | 1 6 |
*P(s;m,n-2)*G(m,n;m,n-2)*T(m,n-2)+ | 1 6 |
*P(s;m,n+2)*G(m,n;m,n+2)*T(m,n+2)+ | 1 6 |
*P(s;m+1,n-1)*G(m,n;m+1,n-1)*T(m+1,n-1)+ | 1 6 |
*P(s;m+1,n+1)*G(m,n;m+1,n+1)*T(m+1,n+1)+ | 1 6 |
*P(s+1;m,n)*F(m,n)*T(m,n)+ | 1 6 |
*P(s;m,n)*F(m,n)*{1-T(m,n)} |
ここで
T(m,n)=1 点(m,n)にトラップがない
T(m,n)=0 点(m,n)にトラップがある
最後に追加した項はその点につかまりっぱなしであることを表す。
問題1では T(0,0)=0 その他は1
このまま適用すると原点から動かないので題意に沿うようにステップ1からの発展を考える。
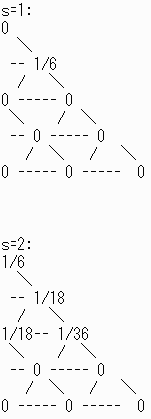
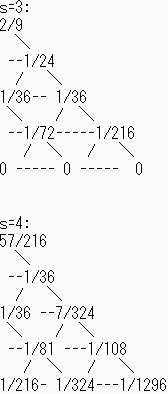
s=5:
| P(5;0,0)= | 57 216 |
+ | 1 36 |
= | 63 216 |
= | 7 24 |
| 答え | 7 24 |
【問題2】
問題1では(0,0)に設けたトラップをこの問題では(2,0)と(2,2)に設ける。
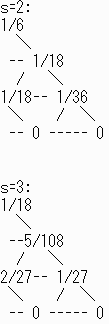
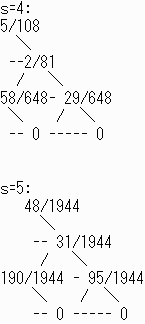
求める確率は他のピースの分もあわせ
| ( | 190 1944 |
+ | 95 1944 |
)*6 = | 95 108 |
| 答え | 95 108 |
【問題3】
各点ともトラップがないとして先の漸化式から値を出す。
s=2までは問題2と共通で
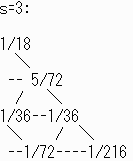
よって他のピースの分も考え存在確率は
| 赤: | 1 18 |
| 青: | 5 72 |
*6 = | 5 12 |
| 黄:( | 1 36 |
+ | 1 36 |
)*6 = | 1 3 |
◆出題者のコメント。
解答ありがとうございます。
すべて正解です。
小学生にも可能な、こんな解法もあります。
【問題3】
3回移動させるので216(=6x6x6)個のコマを最初赤点に置いたものとします。
そこで、移動方向は均等なので各交点にあるコマのすべてを、移動毎に6方向に等しく分配します。
各回の移動において、移動後の各交点の新コマ数は、
| 移動前に隣6方向にあった旧コマ数の合計の | 1 6 |
になる筈です。 |

| ∴ 赤点に存在する確率= | 12×1 216 |
= | 1 18 |
| ∴ 青点に存在する確率= | 15×6 216 |
= | 5 12 |
| ∴ 黄点に存在する確率= | 6×12 216 |
= | 1 3 |
【問題1】【問題2】
【問題3】と同様なやり方で移動をさせ、1回の移動が済むたびに指定点に存在するコマがあれば取り除きます。
取り除かれた全コマ数が元々あったコマ数に対して占める割合が求める確率になります。